مهندسی بی‌نهایت: شزم؛ تجلی قدرت فیزیک در دنیای موسیقی

آیا تاکنون در خصوص سازوکار سرویس تشخیص موسیقی شزم کنجکاو شده‌اید؟ با توجه به مقاله‌ی پژوهشی منتشرشده توسط یکی از بنیان‌گذاران شزم، به‌نام آوری لی-چون ونگ، فرآیندی موسوم به «شناسایی هویت صوتی»، پایه‌ی تمام پردازش‌های صورت‌گرفته در پس سرویس شزم محسوب می‌شود؛ اما شناسایی هویت صوتی به چه مفهوم است؟ با زومیت همراه باشید تا سازوکار شزم را زیر ذره‌بین قرار دهیم.

تماشا در یوتیوب

برای درک آنچه در این مقالات خواهد آمد، باید به‌صورت ابتدایی با مفاهیمی همچون پردازش سیگنال آشنا شویم؛ از این رو در ابتدا کار خود را با مفاهیم پایه‌ای تئوری موسیقی و پردازش سیگنال آغاز می‌کنیم و با مکانیزم‌های موجود در بطن شزم، آن را به پایان می‌رسانیم. برای مطالعه‌ی این مقاله‌ی طولانی به دانشی نیاز نخواهید داشت؛ اما از آنجایی که با علوم کامپیوتر و ریاضیات درگیر خواهیم بود، بهتر است که پس‌زمینه‌ی علمی مناسبی را به‌خصوص برای مطالعه‌ی بخش‌های پایانی داشته باشید. چنانچه با واژه‌هایی همچون اُکتاو، فرکانس، نمونه‌برداری و نشت طیفی آشنایی دارید، می‌توانید از مطالعه‌ی بخش اول صرف‌نظر کنید. شما می‌توانید از فهرست مطالب برای دسترسی سریع‌تر به موضوعات استفاده کنید.

صوت، ارتعاش یا موجی است که از طریق هوا یا آب منتشر شده و توسط گوش ادراک می‌شود؛ به‌عنوان مثال هنگامی که در حال گوش‌دادن به موسیقی هستید، هدفون‌ها ارتعاشاتی را تولید می‌کنند که تا زمان رسیدن به گوش شما، از طریق هوا منتشر می‌شوند. از دیدگاه موجی، نور نیز یک ارتعاش محسوب می‌شود؛ اما به‌جای گوش، چشم توانایی ادراک آن را دارد. یک ارتعاش را می‌توان از طریق موج‌های سینوسی‌ مدل‌سازی کرد. در این قسمت سعی داریم تا با چگونگی توصیف فیزیکی و فنی موسیقی آشنا شویم.

تن خالص، تُنی با شکل موج سینوسی است، امواج سینوسی توسط مشخصه‌های زیر توصیف می‌شود:

• فرکانس موج: تعداد سیکل‌ها در هر ثانیه با واحد هرتز (Hz)، به‌عنوان مثال ۱۰۰ هزتر معادل ۱۰۰ سیکل در هر ثانیه است
• دامنه‌ی موج (مرتبط با بلندی صوت): ابعاد هر سیکل

مشخصه‌های یادشده توسط گوش انسان در قالب صوت ادراک می‌شود. گوش انسان در بهترین حالت،‌ تن‌های خالص با فرکانس ۲۰ تا ۲۰٬۰۰۰ هرتز را می‌شنود؛ اما این بازه با گذر زمان و افزایش سن انسان، محدودتر می‌شود. برای مقایسه باید اشاره کنیم که نور از موج‌های سینوسی با فرکانس بین ۱۰۱۴ × ۴ تا ۱۰۱۴ × ۷.۹ هرتز تشکیل می‌شود.

شما می‌توانید محدوده‌ی شنوایی خود را با ویدیوی زیر بررسی کنید، این ویدیو، تمام تن‌های حقیقی بین ۲۰ هرتز تا ۲۰ کیلوهرتز را تولید می‌کند. من در این ویدیو قادر به شنیدن محدوده‌ی ۲۰ تا ۱۸ هزار هرتز بودم.

ادراک انسان از بلندی صدا به فرکانس تن خالص بستگی دارد؛ به‌عنوان مثال، یک تن خالص با دامنه‌‌ی ۱۰ و فرکانس ۳۰ هرتز، آرام‌تر از تن خالص دیگری با دامنه‌ی ۱۰ و فرکانس ۱۰۰۰ هرتز به گوش می‌رسد. گوش انسان از یک مدل سایکوآکوستیک تبعیت می‌کند که در این مقاله می‌توانید، اطلاعات بیش‌تری را درباره‌ی آن به‌دست آورید. در تصویر زیر می‌توانید نمونه‌ای از یک موج سینوسی با فرکانس ۲۰ هرتز و دامنه‌ی یک را مشاهده کنید:

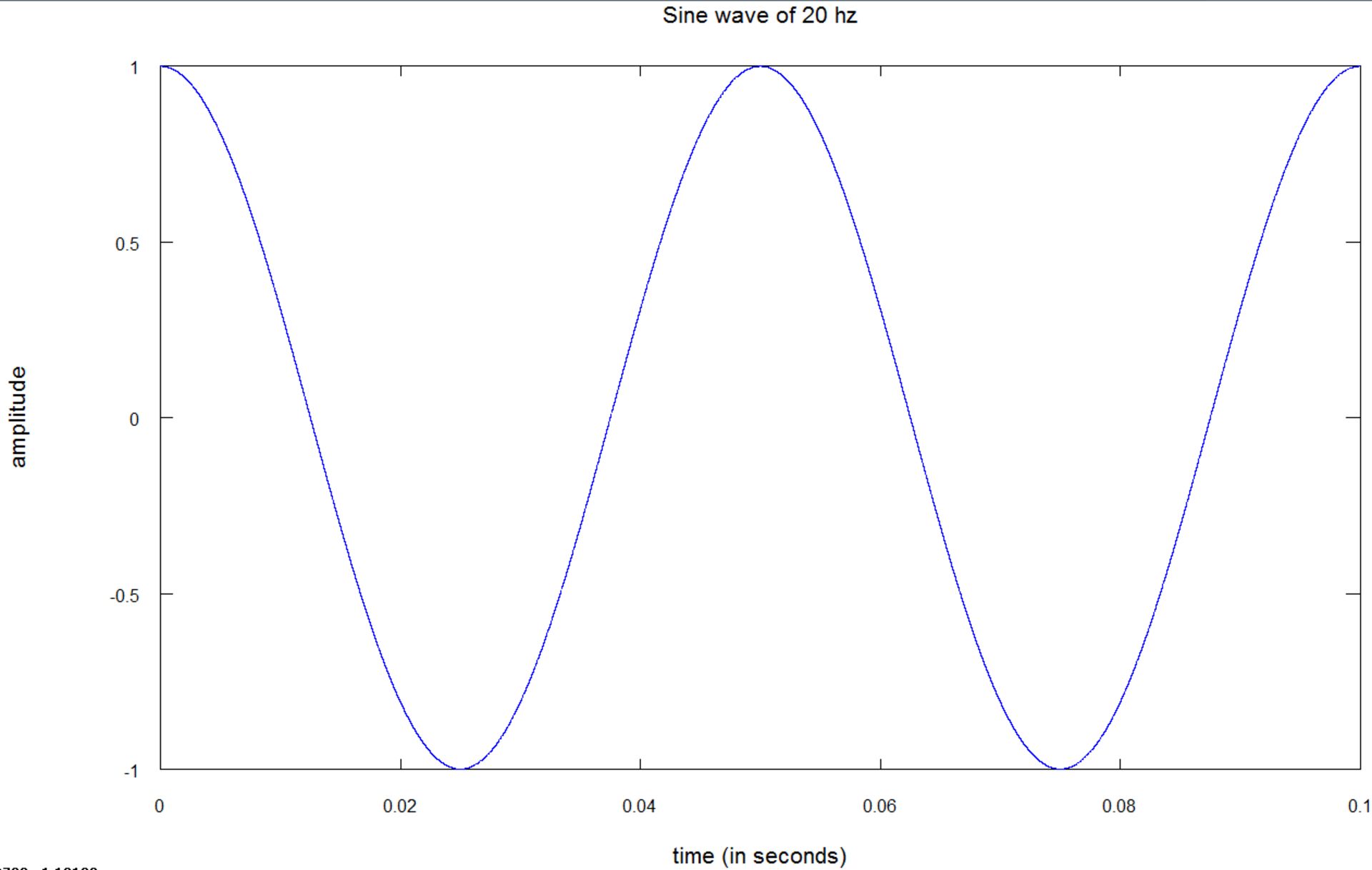
باید بدانید که تن‌های خالص در دنیای واقعی وجود ندارند و آنچه ما به‌صورت روزمره می‌شنویم، ترکیبی از چندین تن خالص با دامنه‌های متفاوت است.

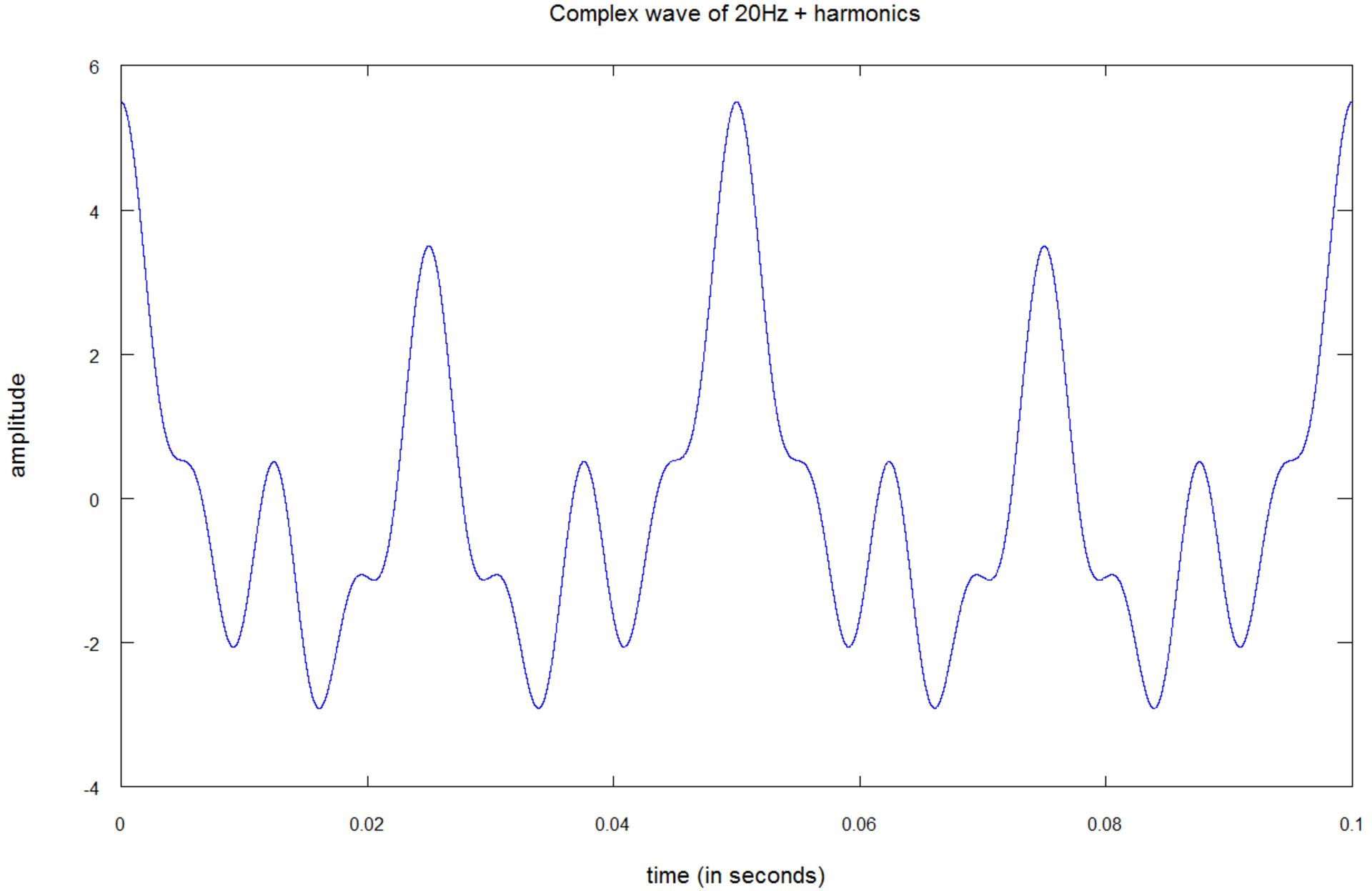
در تصویر بالا می‌توانید نمونه‌ای از صدای حقیقی را مشاهده کنید که از ترکیب چندین موج سینوسی شکل گرفته است:

• یک موج سینوسی خالص با فرکانس ۲۰ هرتز و دامنه‌ی یک؛
• یک موج سینوسی خالص با فرکانس ۴۰ هرتز و دامنه‌ی ۲؛
• یک موج سینوسی خالص با فرکانس ۸۰ هرتز و دامنه‌ی ۱.۵؛
• یک موج سینوسی خالص با فرکانس ۱۶۰ هرتز و دامنه‌ی یک؛

صداهای واقعی می‌توانند ترکیبی از هزاران تن خالص باشند.

نت‌های موسیقی

هر قطعه‌ی موسیقی حاصل مجموعه‌ای از نت‌ها است که در زمان به‌خصوصی اجرا می‌شوند، هرکدام از این نت‌ها مدت‌زمان و بلندی منحصربه‌فردی دارند.

مجموعه‌ی نت‌ها در قالب اکتاو‌هایی تقسیم می‌شوند. در کشورهای غربی، هر اکتاو، مجموعه‌ای از ۸ نت (ای، بی‌، سی، دی، ایی، اف، جی در بسیاری از کشورهای انگلیسی‌زبان و دو – ر – می – فا – سُل – لا – سی در کشورهای لاتین غربی) محسوب می‌شود. ویژگی اکتاوها بدین شرح است:

• فرکانس هر نت در یک اکتاو در اکتاو بعدی دو برابر می‌شود؛ به‌عنوان مثال فرکانس A4 (نت A در اکتاو چهارم) در ۴۴۰ هرتز دو برابر فرکانس A3 (نت A در اکتاو سوم) در ۲۲۰ هرتز بوده و چهار برابر فرکانس A2 (نت A در اکتاو دوم) در ۱۱۰ هرتز است.

بسیاری از آلات موسیقی، بیش از ۸ نت را در اکتاوها فراهم می‌کنند، چنین نت‌هایی سمی‌تُن یا نیم‌‌پرده نامیده می‌شوند.

برای اکتاو چهارم (یا اکتاو سوم در کشورهای لاتین غربی)، فرکانس نت‌ها بدین شکل است:

• C4 (Do3) = ۲۶۱.۳ هرتز
• D4 (Re3) = ۲۹۳.۶۷ هرتز
• E4 (Mi3) = ۳۲۹.۶۳ هرتز
• F4 (Fa3) = ۳۴۹.۲۳ هرتز
• G4 (Sol3) = ۳۹۲ هرتز
• A4 (La3) = ۴۴۰ هرتز
• B4 (Si3) = ۴۹۳.۸۸ هرتز

اگرچه ممکن است عجیب به‌نظر برسد؛ اما حساسیت فرکانسی گوش انسان، لگاریتمی است؛ بدین مفهوم:

• بین ۳۲.۷۰ هرتز و ۶۱.۷۴ هرتز (اکتاو اول)
• یا بین ۲۶۱.۶۳ هرتز و ۴۶۶.۱۶ هرتز (اکتاو چهارم)
• یا بین ۲۰۹۳ هرتز و ۳۹۵۱.۰۷ هرتز (اکتاو هفتم)

گوش‌های انسان قادر به تشخیص تعداد یکسانی از نت‌ها هستند. خاطرنشان می‌کنیم که نت‌  A4/La3 در فرکانس ۴۴۰ هرتز، مرجعی استاندارد برای کالیبره‌سازی ابزار آکوستیک و آلات موسیقی محسوب می‌شود.

نواختن یک نت با گیتار، پیانو، ویولون یا یک هنرمند، به تولید صدای یکسانی منجر نمی‌شود؛ زیرا هر آلت موسیقی، طنین منحصربه‌فردی برای یک نت دلخواه دارد. برای هر آلت موسیقی، صدای تولیدشده، انبوه فرکانس‌هایی است که مشابه یک نت دلخواه (نام علمی نت موسیقی، نواک است) به گوش می‌رسند. این صدا، یک فرکانس پایه‌ (کم‌ترین فرکانس) و چندین Overtone یا نت فرعی (هر فرکانسی بالاتر از فرکانس پایه) را در برمی‌گیرد.

بسیاری از آلت‌های موسیقی صداهای نزدیک به هارمونیک (همساز) را تولید می‌کنند. برای چنین ابزارهایی، نت‌های فرعی، چندین فرکانس پایه با نام هارمونیک هستند؛ به‌عنوان مثال، ترکیب تن‌های خالص A2 (پایه)، A4 و A6 هارمونیک هستند؛ اما ترکیب تن‌های خالص A2، B3 و F5 غیرهارمونیک یا ناهمساز است. بسیاری از سازهای کوبه‌ای، مانند درام یا سنج، صداهای غیرهارمونیک تولید می‌کنند.

خاطرنشان می‌کنیم که نواک (نت موسیقی ادراک‌شده)، ممکن است در صدای تولیدشده توسط یک ساز به‌خصوص وجود نداشته باشد؛ به‌عنوان مثال، چنانچه یک ساز صدایی با تن‌های خالص A4، A6 و A8 را تولید ‌کند، مغز انسان صدای حاصل را در قالب یک نت A2 تشریح می‌کند. در حالتی که پایین‌ترین فرکانس در صدا A4 باشد، نت / نواک یک A2 خواهد بود، به این پدیده، از دست رفتن فرکانس پایه گفته می‌شود.

یک قطعه‌ی موسیقی توسط چندین ساز و هنرمند نواخته می‌شود، تمام این سازها، ترکیبی از موج‌های سینوسی در چندین فرکانس را تولید می‌کنند و در مجموع، صدای تولیدشده از ترکیب موج‌های سینوسی به‌مراتب بزرگ‌تری تشکیل می‌شود. می‌توان با یک طیف‌نگاره، موسیقی را مشاهده کرد. در اغلب اوقات، طیف‌نگاره نموداری سه‌بعدی است:

• زمان روی محور افقی X قرار می‌گیرد
• فرکانس تن‌های خالص روی محور عمودی Y قرار می‌گیرد
• بُعد سوم با یک رنگ توصیف می‌شود و دامنه‌ی یک فرکانس را در زمان به‌خصوصی نشان می‌دهد.

نمودار زیر، طیف‌نگاره‌ی مربوط به صدای پیانو را نشان می‌دهد. رنگ‌ها در طیف‌نگاره، دامنه‌ی صدا را برحسب دسی‌بل نشان می‌دهند.

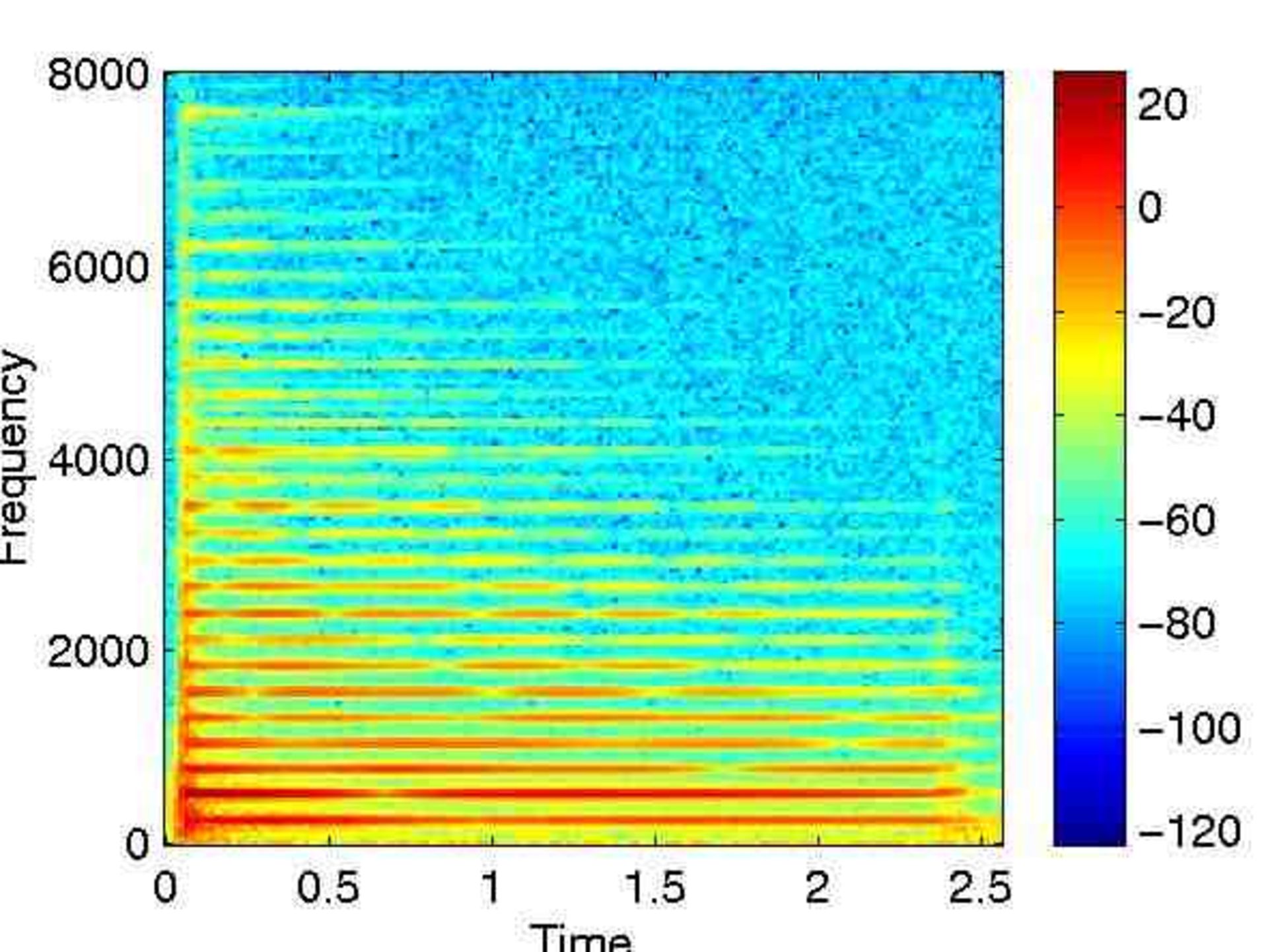
نکته‌ی جالب توجه دیگر، تغییر شدت فرکانس‌ها با گذر زمان است، این موضوع یکی دیگر از ویژگی‌های یک ساز محسوب می‌شود که آن را منحصربه‌فرد می‌کند. اگر نوازنده به‌جای پیانو، ساز دیگری را بنوازد، الگوی تکامل فرکانس‌ها متفاوت خواهد بود و صدای حاصل‌شده نیز کمی تفاوت خواهد داشت؛ زیرا هر هنرمند / ساز، استایل منحصربه‌فردی دارد. از لحاظ فنی، این تکامل فرکانسی، محدوده‌ی (envelope) سیگنال صدا را اصلاح می‌کند و این محدوده بخشی از طنین محسوب می‌شود.

برای آنکه ایده‌ای ابتدایی از نوع کارکرد پروسه‌ی شناسایی هویت صوتی در شزم به‌دست آورید، توجه شما را به طیف‌نگاره‌ی بالا جلب می‌کنیم که در آن برخی از فرکانس‌ها (نمونه‌هایی پایین) اهمیت بیشتری نسبت به بقیه دارند. اگر تنها فرکانس‌های قدرتمند را نگه داریم، چه پیش می‌آید؟

مادامی که از علاقه‌مندان به صفحه‌ی گرامافون نباشید، هنگام گوش دادن به موسیقی از فایل‌های دیجیتال (mp3، سی‌دی صوتی، ogg یا apple lossless) استفاده می‌کنید؛ اما هنرمندان موسیقی را به‌صورت آنالوگ تولید می‌کنند؛ بدین مفهوم که موسیقی آن‌ها در قالب بیت نیستند. برای آنکه موسیقی قابل ذخیره‌سازی یا پخش‌شدن در دستگاه‌های الکترونیکی باشد، باید به‌صورت دیجیتال باشد. در این بخش با چگونگی گذار از آنالوگ به دیجیتال آشنا می‌شویم. آگاهی از چگونگی تولید موسیقی دیجیتال به ما در بخش‌‌های بعدی جهت تحلیل یا دست‌کاری آن کمک خواهد کرد.

سیگنال‌های آنالوگ پیوسته هستند؛ بدین مفهوم که اگر شما یک ثانیه از سیگنال آنالوگی را انتخاب کنید، می‌توانید آن را به بی‌شمار قسمت تقسیم کنید. در دنیای دیجیتال، نمی‌توان بی‌نهایت اطلاعات را ذخیره کرد؛ از این رو باید یک واحد حداقلی، نظیر یک میلی‌ثانیه در اختیار داشته باشید. در طول این واحد از زمان، صوت نمی‌تواند تغییر کند؛ بنابراین واحد زمان باید به‌اندازه‌ای کوتاه باشد که موسیقی دیجیتال شبیه به نمونه‌ی آنالوگ باشد و به‌اندازه‌ای طولانی باشد که بتوان فضای مورد نیاز برای ذخیره‌ی موسیقی را محدود کرد.

به‌عنوان مثال، موسیقی مورد علاقه‌ی خود را به‌خاطر بیاورید؛ حال تصور کنید که صدا در این موسیقی هر ۲ ثانیه یک بار تغییر کند، بی‌شک نتیجه‌ی نهایی هیچ شباهتی به نمونه‌ی اصلی نخواهد داشت. در چنین شرایطی به‌لحاظ فنی گفته می‌شود که صدا Aliased شده است؛ این پدیده زمانی رخ می‌دهد که فرکانس نمونه‌برداری کمتر از دو برابر فرکانس بیشینه‌ی موجود در صوت باشد.

برای آنکه از کیفیت صدای موسیقی اطمینان حاصل کنیم، باید واحد نمونه‌برداری را بسیار کوچک، به‌عنوان مثال در حد یک نانو ثانیه (۹- ۱۰) انتخاب کنیم، در این شرایط کیفیت صدای حاصل بسیار بالا خواهد بود؛ اما فضای کافی برای ذخیره‌ی موسیقی در اختیار نخواهید داشت. به این فرآیند نمونه‌برداری گفته می‌شود.

واحد استاندارد زمان در موسیقی دیجیتال، ۴۴۱۰۰ نموه به ازای هر ثانیه است؛ اما این فرکانس ۴۴.۱ کیلوهرتزی از کجا آمده؟ در فصل نخست مقاله، گفتیم که انسان در بهترین حالت می‌تواند اصواتی با فرکانس بین ۲۰ تا ۲۰ هزار هرتز را بشنود. براساس قضیه‌ی نایکوئیست، برای آنکه بتوان سیگنالی با فرکانس بین صفر تا ۲۰ هزار هرتز را گسسته‌سازی یا دیجیتال‌سازی کرد، باید در هر ثانیه حداقل ۴۰ هزار بار نمونه‌برداری کرد.

ایده‌ی موجود در پس چنین منطقی آن است که برای قابل شناسایی‌بودن یک سیگنال سینوسی با فرکانس F، باید در هر سیکل آن، حداقل دو نقطه وجود داشته باشد؛ بنابراین چنانچه فرکانس نمونه‌برداری دو برابر فرکانس سیگنال باشد، در هر سیکل از سیگنال ابتدایی، دو نقطه خواهید داشت. برای درک بهتر موضوع به تصویر زیر توجه کنید:

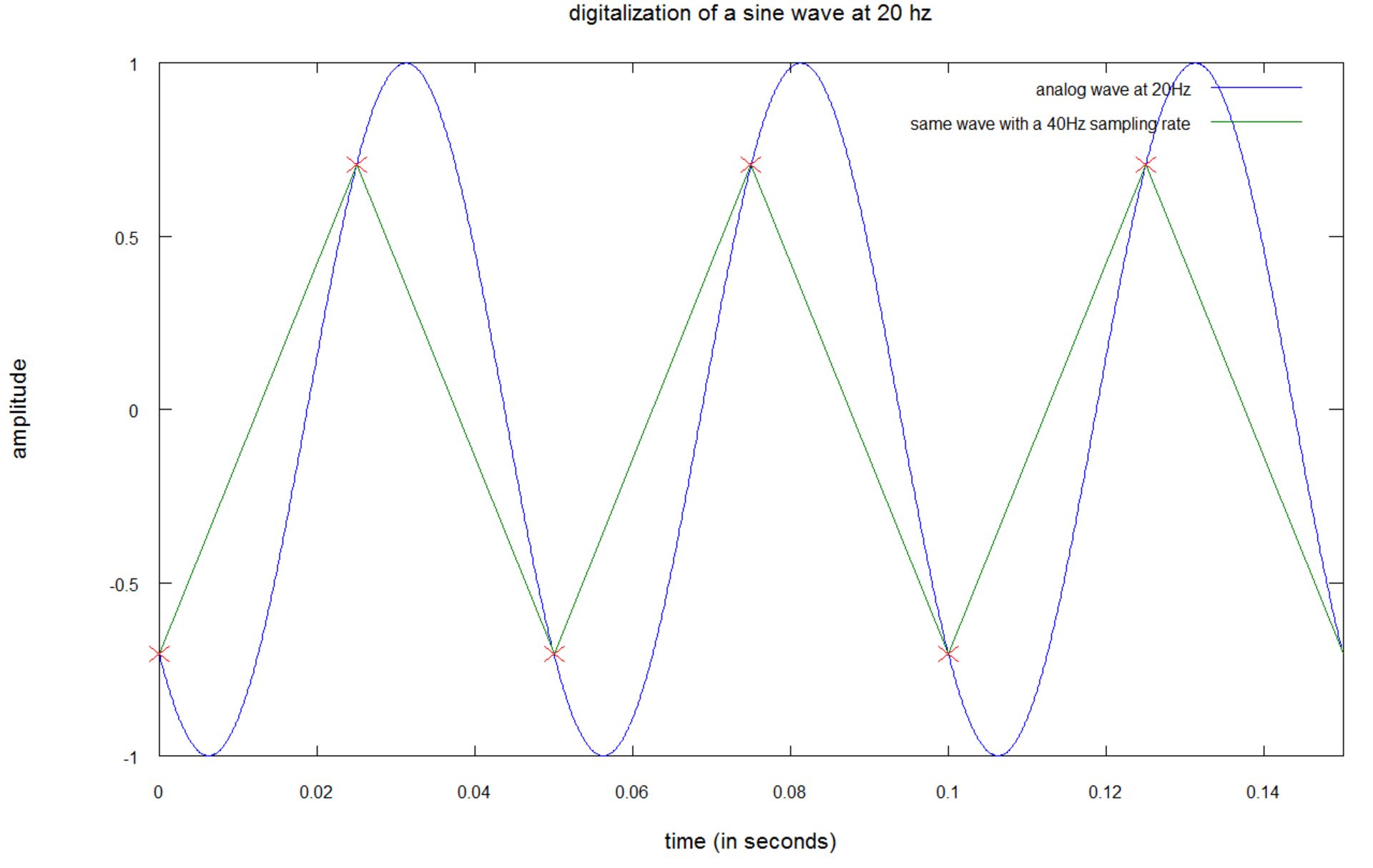
در نمودار بالا، صوتی با فرکانس ۲۰ هرتز با استفاده از نرخ نمونه‌برداری ۴۰ هرتزی، دیجیتال می‌شود.

• منحنی آبی، سیگنال صدا را با فرکانس ۲۰ هرتز نشان می‌دهد
• نقاط قرمز، صداهای نمونه را نشان می‌دهند، بدین مفهوم که در هر ۱/۴۰ ثانیه، یک بار منحنی آبی را با علامت‌های ضرب قرمز، نشانه‌گذاری کرده‌ایم
• خطوط سبز، درون‌یابی صدای نمونه‌برداری شده را به تصویر می‌کشند

اگرچه خطوط حاصل از نمونه‌برداری، فُرم یا دامنه‌ای مشابه منحنی اصلی ندارند؛ اما فرکانس سیگنال نمونه‌برداری‌شده ثابت باقی مانده است. در ادامه توجه شما را به یک نمونه‌برداری مناسب جلب می‌کنیم:

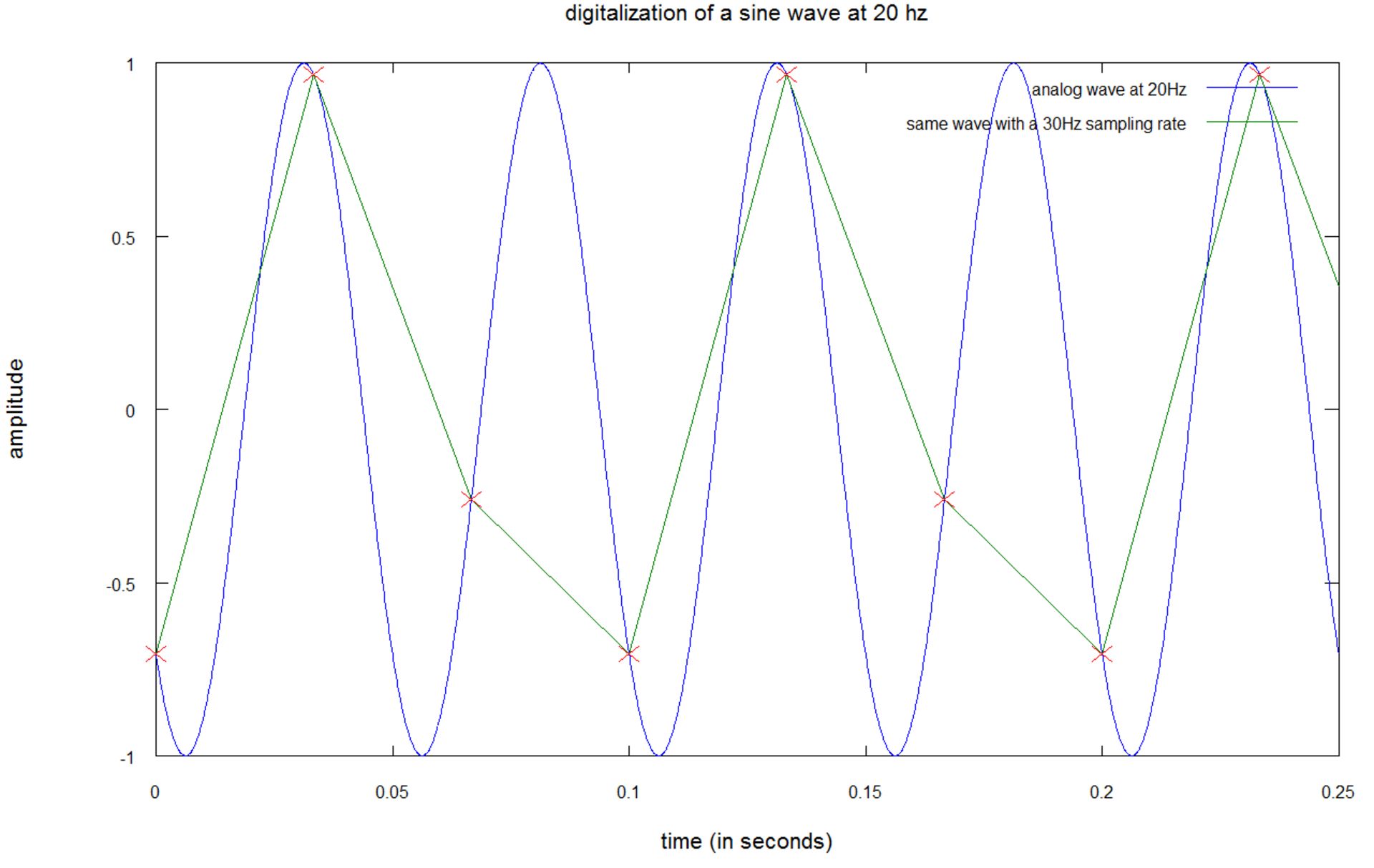
در نمودار بالا صوتی با فرکانس ۲۰ هرتز و سیگنال نمونه‌برداری‌شده‌ای را با فرکانس ۳۰ هرتز مشاهده می‌کنید؛ بدین مفهوم که سیگنال نمونه‌‌برداری‌شده فرکانس یکسانی با سیگنال اصلی ندارد: تنها ۱۰ هرتز فاصله وجود دارد. چنانچه دقیق‌تر نگاه کنید، مشاهده خواهید کرد که یک سیکل در سیگنال نمونه‌برداری‌شده، دو سیکل در سیگنال اصلی را به نمایش می‌گذارد، در این حالت شاهد پدیده‌ی Under Sampling هستیم.

نمودار بالا، موضوع مهم دیگری را نیز به تصویر می‌کشد: چنانچه می‌خواهید سیگنالی بین صفر تا ۲۰ هزار هرتز را دیجیتال کنید، باید پیش از نمونه‌برداری، فرکانس‌های بالاتر از ۲۰ هزار هرتز را از سیگنال حذف کنید، در غیر این‌صورت، فرکانس‌های یادشده پس از نمونه‌برداری به فرکانس‌هایی بین صفر تا ۲۰ هزار هرتز بدل شده و صداهای ناخواسته‌ای را ایجاد خواهند کرد که به این پدیده Aliasing گفته می‌شود.

بنابراین، چنانچه می‌خواهید موسیقی را به‌خوبی از آنالوگ به دیجیتال تبدیل کنید، باید حداقل نرخ نمونه‌برداری ۴۰ هزار بار در ثانیه را انتخاب کنید. شرکت‌هایی همچون سونی در طول دهه‌ی ۹۰ فرکانس ۴۴.۱ کیلوهرتز را انتخاب کردند؛ زیرا بالاتر از ۴۰ هزار هرتز است و با فرمت‌های تصویری NTSC و PAL سازگاری دارد؛ البته استانداردهای دیگری همچون ۴۸ کیلوهرتز (بلوری)، ۹۶ کیلوهرتز یا ۱۹۲ کیلوهرتز نیز وجود دارند؛ اما چنانچه حرفه‌ای یا به اصطلاح خوره‌ی صدا نیستید، به احتمال زیاد، موسیقی را با نرخ ۴۴.۱ کیلوهرتز گوش می‌دهید.

نکته‌ی ۱: قضیه‌ی نایکوئیست مبحث بسیار گسترده‌ای است، برای کسب اطلاعات بیشتر می‌توانید به مراجع پردازش سیگنال یا صفحه‌ی ویکیپدیای این قضیه مراجعه کنید.

نکته‌ی ۲: برای دیجتالی‌سازی، فرکانس نمونه‌برداری باید اکیدا بزرگتر از دو برابر فرکانس سیگنال باشد؛ زیرا در بدترین حالت، ممکن است با یک سیگنال دیجیتالی ثابت طرف باشیم.

 در بخش قبل، با چگونگی دیجیتالی‌سازی فرکانس‌های موسیقی آنالوگ آشنا شدیم؛ اما بلندی صدای موسیقی چگونه خواهد بود؟ بلندی صدا معیاری نسبی است: به ازای بلندی صدای یکسان درون سیگنال، چنانچه حجم صدای اسپیکر را افزایش دهید، شدت صدای موسیقی افزایش خواهد یافت. بلندی صدا، به تفاوت بین پایین‌ترین و بالاترین سطح صدا در یک قطعه‌ی موسیقی گفته می‌شود.

مشکل پیشین در مورد بلندی صدا نیز پیش می‌آید: گذار از دنیای پیوسته با بی‌نهایت تغییر در حجم به دنیای گسسته چگونه صورت می‌گیرد؟

موسیقی مورد علاقه‌ی خود را با چهار سطح بلندی «بدون صدا»، «صدای پایین»، «صدای بلند» و «تمام توان» تصور کنید، در چنین وضعیتی، حتی بهترین موسیقی دنیا نیز غیرقابل تحمل خواهد بود. آنچه تصور کردید، کوانتیده‌سازی با ۴ سطح بود. در تصور زیر می‌توانید نمونه‌ای از کوانتیده‌سازی سطح پایین را مشاهده کنید:

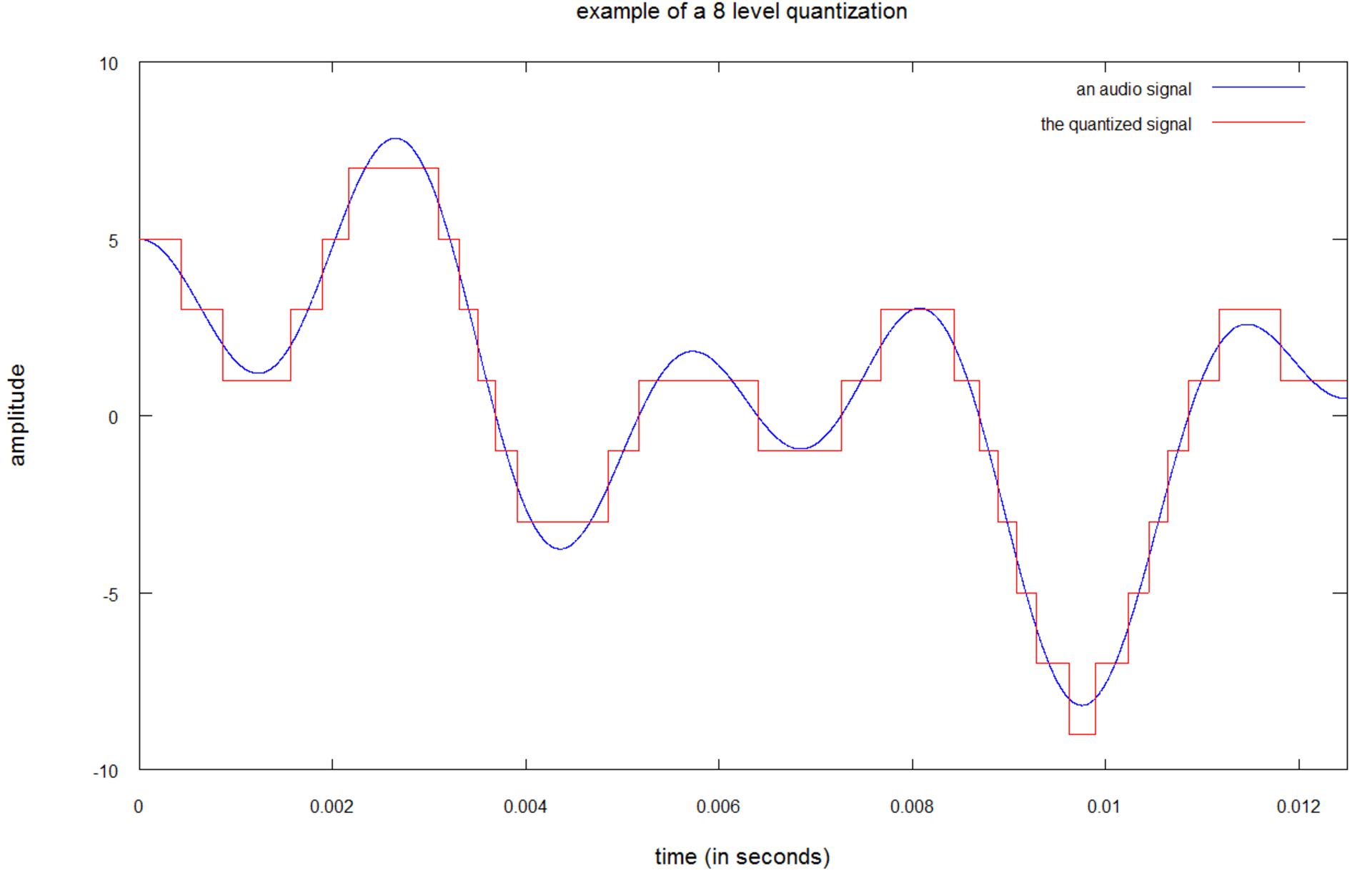
این تصویر، کوانتیده‌سازی با ۸ سطح را نشان می‌دهد. همان‌طور که مشاهده می‌کنید، صدای حاصل با رنگ قرمز، تفاوت فاحشی با نمونه‌ی اصلی دارد. تفاوت بین صدای واقعی و نمونه‌ی کوانتیده‌شده، خطای کوانتیده‌سازی یا نویز کوانتیده‌سازی نامیده می‌شود. کوانتیده‌سازی ۸ سطحی با نام کوانتیده‌سازی ۳ بیتی نیز نامیده می‌شود؛ زیرا شما تنها به ۳ بیت برای پیاده‌سازی ۸ سطح مختلف نیاز خواهید داشت (۸ = ۲۳). 

در تصویر زیر همان سیگنال را با کوانتیده‌سازی ۶۴ سطحی یا کوانتیده‌سازی ۶ بیتی مشاهده می‌‌کنید. اگرچه صدای حاصل باز هم متفاوت به‌نظر می‌رسد؛ اما شباهت بیشتری به صدای اصلی دارد.

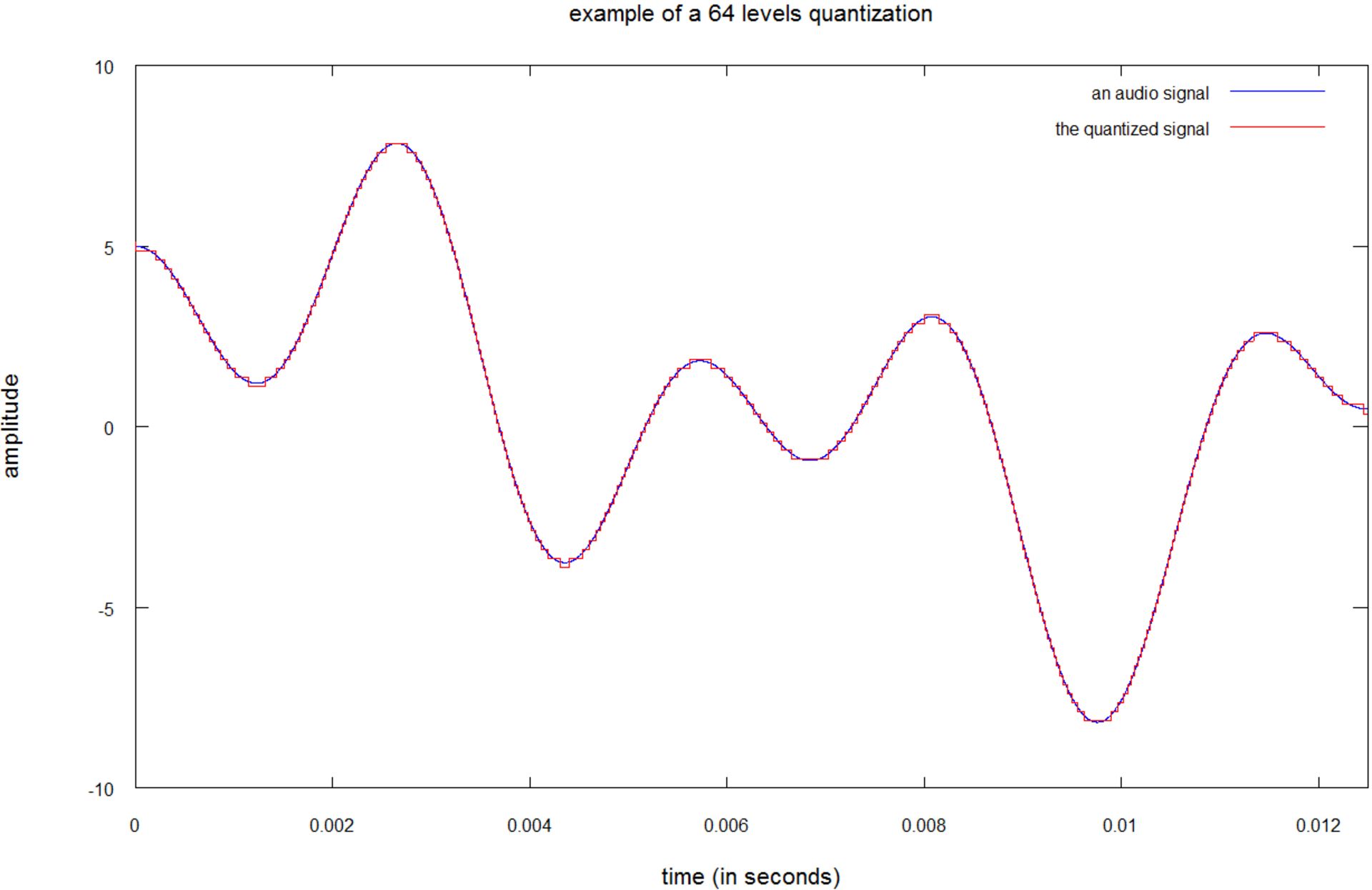
خوشبختانه گوش انسان‌ها حساسیت فوق‌العاده بالایی ندارد؛ از این رو کوانتیده‌سازی ۱۶ بیتی یا ۶۵۵۳۶ سطحی به‌عنوان استاندارد تعریف می‌شود. با کوانتیده‌سازی ۱۶ بیتی، نویز کوانتیده‌سازی برای گوش انسان‌ها به‌اندازه‌ی کافی در سطح پایینی قرار دارد.

نکته‌ی ۱: در استودیوهای ضبط موسیقی، حرفه‌ای‌ها از کوانتیده‌سازی ۲۴ بیتی استفاده می‌کنند؛ بدین مفهوم که بین بالاترین و پایین‌ترین بلندی صدا، ۲۲۴ یا ۱۶ میلیون تغییر ممکن وجود دارد.

نکته‌ی ۲: در مثال‌های ارائه‌شده در خصوص تعداد سطح‌های کوانتیده‌سازی، تقریب‌هایی صورت گرفته است.

PCM یا مدولاسیون کُد پالس، استانداردی است که سیگنال‌های دیجیتال را به‌تصویر می‌کشد. این استاندارد در دیسک‌های فشرده و بسیاری از دستگاه‌های الکترونیکی به‌کار می‌رود؛ به‌عنوان مثال، هنگامی که به یک فایل mp3 در کامیپوتر، گوشی هوشمند یا تبلت خود گوش می‌دهید، آن فایل به‌صورت خودکار به سیگنال PCM تبدیل شده و به هدفون شما ارسال می‌شود.

جریان PCM، جریانی از بیت‌های سازمان‌دهی شده است، این جریان می‌تواند از چندین کانال تشکیل شده باشد؛ به‌عنوان مثال، یک قطعه‌ی موسیقی استریو، دو کانال دارد. در یک جریان، دامنه‌ی سیگنال به نمونه‌هایی تقسیم می‌شود. تعداد نمونه‌ها به ازای هر ثانیه، با نرخ نمونه‌برداری موسیقی هماهنگی دارد؛ به‌عنوان مثال، یک قطعه‌ی موسیقی با نرخ نمونه‌برداری ۴۴۱۰۰ هرتزی، در هر ثانیه ۴۴۱۰۰ نمونه خواهد داشت. هر نمونه، دامنه‌ی صدای کوانتیده‌ی مربوط به کسری از ثانیه‌ها را در بر دارد.

فرمت‌های PCM گوناگونی وجود دارد؛ اما رایج‌ترین نمونه برای صدا، فرمت خطی PCM استریو با فرکانس ۴۴.۱ کیلوهرتز و عمق ۱۶ بیت است، این فرمت ۴۴۱۰۰ نمونه در هر ثانیه از موسیقی را در بر دارد و هر نمونه، ۴ بیت را اشغال می‌کنند.

• ۲ بایت (۱۶ بیت) برای شدت صدای (از ۳۲٬۷۶۸- تا ۳۲٬۷۶۷) اسپیکر سمت چپ
• ۲ بایت (۱۶ بیت) برای شدت صدای (از ۳۲٬۷۶۸- تا ۳۲٬۷۶۷) اسپیکر سمت راست

در فرمت استریوی PCM با فرکانس ۴۴.۱ کیلوهرتز و عمق ۱۶ بیت، در هر ثانیه از موسیقی، ۴۴۱۰۰ نمونه مانند تصویر بالا خواهید داشت.

شما اکنون از چگونگی گذار از صدای آنالوگ به دیجیتال آگاهی دارید؛ اما چگونه می‌توان فرکانس‌های موجود داخل یک سیگنال دیجیتال را به‌دست آورد؟ این بخش از اهمیت بسیار بالایی برخوردار است؛ زیرا الگوریتم شناسایی هویت صوت شزم تنها با فرکانس‌ها کار می‌کند.

برای سیگنال‌های پیوسته یا آنالوگ، راهکاری موسوم به تبدیل فوریه وجود دارد. با استفاده از این راهکار، می‌توان تابع زمان را به تابع فرکانس تبدیل کرد. به‌عبارت دیگر، چنانچه شما تبدیل فوریه را روی یک صوت به‌کار ببرید، این تبدیل، فرکانس‌های موجود در این صوت و شدت آن‌ها را در اختیار شما خواهد گذاشت؛ اما در این مسیر، دو مشکل وجود دارد:

• ما با صداهای دیجیتال یا به‌عبارت بهتر صداهای متناهی (ناپیوسته) سروکار داریم
• برای آگاهی از فرکانس‌های موجود در موسیقی، باید تبدیل فوریه را روی قسمت‌های کوتاهی از کل سیگنال صوتی به‌کار ببریم؛ به‌عنوان مثال یک قسمت ۰.۱ ثانیه‌ای تا بدین ترتیب بدانیم که در هر ۰.۱ ثانیه از قطعه‌ی موسیقی چه فرکانس‌هایی وجود دارد

خوشبختانه تابع ریاضی دیگری موسوم به تبدیل گسسته‌ی فوریه (DFT) وجود دارد که با چنین محدودیت‌هایی سازگار است.

نکته: تبدیل فوریه باید تنها روی یک کانال اِعمال شود؛ بنابراین چنانچه یک قطعه‌ی موسیقی استریو داشته باشید، باید آن را به قطعه‌ی مونو (تک کاناله) تبدیل کنید.

تبدیل فوریه‌ی گسسته روی سیگنال‌های گسسته اِعمال می‌شود و طیفی گسسته از فرکانس‌های موجود در سیگنال را ارائه می‌دهد. رابطه‌ی جادویی زیر، سیگنال دیجیتال را به فرکانس‌ها بدل می‌کند:

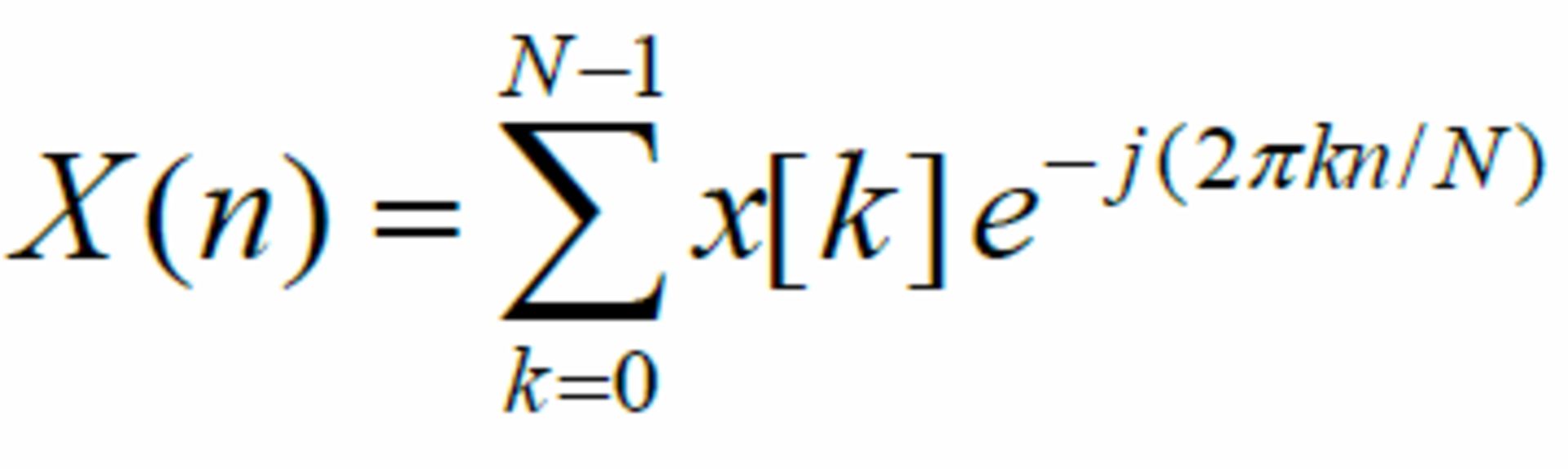
در رابطه‌ی بالا:

• N ابعاد پنجره را نشان می‌دهد: تعداد نمونه‌هایی که سیگنال را شکل می‌دهند (در رابطه به‌صورت مفصل راجع به پنجره‌ها بحث خواهیم کرد)
• X(n) نشان‌دهنده‌ی nامین بازه‌ی فرکانسی است
• X(k) نشان‌دهنده‌ی kامین نمونه‌ی سیگنال صوتی است

به‌عنوان مثال برای یک سیگنال صوتی با پنجره‌ی ۴۰۹۶ نمونه‌ای، رابطه‌ی یادشده باید ۴۰۹۶ بار به کار گرفته شود:

• یک بار برای n = 0 جهت محاسبه‌ی بازه‌ی صفرم فرکانسی
• یک بار برای n = 1 جهت محاسبه‌ی بازه‌ی اول فرکانسی
• یک بار برای n = 2 جهت محاسبه‌ی بازه‌ی دوم فرکانسی
• ...

همان‌طور که احتمالا متوجه شده‌اید، به‌جای فرکانس، در خصوص بازه‌ی فرکانسی صحبت کردیم؛ زیرا DFT طیف گسسته ارائه می‌دهد. بازه‌ی فرکانسی، کوچکترین واحد فرکانسی است که DFT می‌تواند محاسبه کند. اندازه‌ی این بازه (وضوح طیف / طیفی یا وضوح فرکانسی) برابر با نرخ نمونه‌برداری سیگنال تقسیم بر اندازه‌ی پنجره (N) است. در مثال ما، با پنجره‌ی ۴۰۹۶ نمونه‌ای و نرخ نمونه‌برداری صوتی استاندارد ۴۴.۱ کیلوهرتزی، وضوح فرکانسی معادل ۱۰.۷۷ هرتز است (به‌جز بازه‌ی صفرم که استثناء محسوب می‌شود):

• بازه‌ی صفرم فرکانس‌های بین ۰ تا ۵.۳۸ هرتز را نشان می‌دهد
• بازه‌ی اول فرکانس‌های بین بین ۵.۳۸ تا ۱۶.۱۵ هرتز را نشان می‌دهد
• بازه‌ی دوم فرکانس‌های بین ۱۶.۱۵ تا ۲۶.۹۲ هرتز را نشان می‌دهد
• بازه‌ی سوم فرکانس‌های بین ۲۶.۹۲ تا ۳۷.۶۸ هرتز را نشان می‌دهد
• ...

بنابراین DFT نمی‌تواند دو فرکانس با تفاوت کمتر از ۱۰.۷۷ هرتز را تفکیک کند؛ به‌عنوان مثال، نت‌هایی با فرکانس ۲۷ هرتز، ۳۲ هرتز و ۳۷ هرتز، در بازه‌ی فرکانسی یکسانی قرار می‌گیرند. چنانچه نت در فرکانس ۳۷ هرتز بسیار قدرتمند باشد، شما تنها متوجه خواهید شد که بازه‌ی سوم قدرتمند است، این موضوع بر سر تفکیک نت‌ها در پایین‌ترین اکتاوها مشکل‌ساز خواهد بود؛ به‌عنوان مثال:

• نت A1 / La1 در فرکانس ۵۵ هرتز قرار دارد، در حالی که نت B1 / Si1 و نت G1 / Sol1 به‌ترتیب در فرکانس‌های ۵۸.۲۷ و ۴۹ هرتز قرار دارند
• نت اول در یک پیانوی ۸۸ کلیدی استاندارد A0 با فرکانس ۲۷.۵ هرتز و به دنبال آن، A#0 با فرکانس ۲۹.۱۴ هرتز است

شما می‌توانید وضوح فرکانسی را با افزایش ابعاد پنجره بهبود دهید؛ اما در این حالت تغییرات سریع فرکانس / نت را در موسیقی از دست خواهید داد:

• یک سیگنال صوتی نرخ نمونه‌برداری ۴۴.۱ کیلوهرتزی دارد
• افزایش ابعاد پنجره به مفهوم گرفتن نمونه‌های بیشتر و به‌دنبال آن، افزایش مدت‌زمان صرف‌شده توسط پنجره است
• با ۴۰۹۶ نمونه، مدت‌زمان پنجره ۰.۱ ثانیه و وضوح فرکانسی ۱۰.۷ هرتز است: شما می‌توانید تغییرات را در هر ۰.۱ ثانیه تشخیص دهید
• با ۱۶۳۸۴ نمونه، مدت‌زمان پنجره ۰.۳۷ ثانیه و وضوح فرکانسی ۲.۷ هرتز است: شما می‌توانید تغییرات را در هر ۰.۳۷ ثانیه تشخیص دهید

یکی دیگر از مشخصات سیگنال صوتی این است که ما تنها به نیمی از بازه‌ی محاسبه‌شده توسط DFT نیاز داریم. در مثال پیشین، وضوح فرکانسی ۱۰.۷ هرتز بود؛ بدین مفهوم که بازه‌ی ۲۰۴۷‌ام فرکانس‌های بین ۲۱۹۰۲.۹ هرتز تا ۲۱۹۱۳.۶ هرتز را در بر می‌گیرد؛ اما:

• بازه‌ی ۲۰۴۸ام اطلاعات یکسانی را با بازه‌ی صفرم ارائه خواهد داد
• بازه‌ی ۲۰۴۹ام اطلاعات یکسانی را با بازه‌ی اول ارائه خواهد داد
• بازه‌ی X + 2048ام اطلاعات یکسانی را با بازه‌ی ایکس ارائه خواهد داد
• ...

چنانچه می‌خواهید دلیل آنکه وضوح فرکانسی معادل نرخ نمونه‌‌برداری تقسیم بر ابعاد پنجره‌است یا دلیل عجیب‌بودن این رابطه را بدانید، توصیه می‌کنیم این مقاله‌ی پنج بخشی درباره‌ی تبدیل فوریه را مطالعه کنید (به‌خصوص بخش‌های چهارم و پنجم)؛ زیرا یکی از بهترین مقالات برای افراد مبتدی مانند ما محسوب می‌شود.

اگر می‌خواهید فرکانس یک صوت یک ثانیه‌ای را در هر بازه‌ی ۰.۱ ثانیه‌ای به‌دست آورید، باید تبدیل فوریه را روی بازه‌ی ۰.۱ ثانیه‌ای اول، بازه‌ی ۰.۱ ثانیه‌ای دوم، بازه‌ی ۰.۱ ثانیه‌ای سوم و غیره پیاده کنید...

اما در این حالت، به‌صورت ضمنی یک تابع پنجره‌ای (مستطیلی) را پیاده می‌کنید:

• برای ۰.۱ ثانیه‌ی نخست، تبدیل فوریه را روی سیگنال یک ثانیه‌ای ضرب‌ در تابعی پیاده می‌کنیم که بین صفر تا ۰.۱ ثانیه معادل «۱» و در باقی زمان‌ها معادل صفر است.
• برای ۰.۱ ثانیه‌ی دوم، تبدیل فوریه را روی سیگنال یک ثانیه‌ای ضرب‌ در تابعی پیاده می‌کنیم که بین ۰.۱ تا ۰.۲ ثانیه معادل «۱» و در باقی زمان‌ها معادل صفر است.
• برای ۰.۱ ثانیه‌ی سوم، تبدیل فوریه را روی سیگنال یک ثانیه‌ای ضرب‌ در تابعی پیاده می‌کنیم که بین ۰.۲ تا ۰.۳ ثانیه معادل «۱» و در باقی زمان‌ها معادل صفر است.
• ...

در تصویر زیر می‌توانید به‌صورت شهودی، اِعمال تابع پنجره‌ای روی یک سیگنال صوتی دیجیتال (نمونه‌برداری‌شده) را برای به‌دست آوردن فرکانس بازه‌ی ۰.۱ ثانیه‌ی نخست را مشاهده کنید:

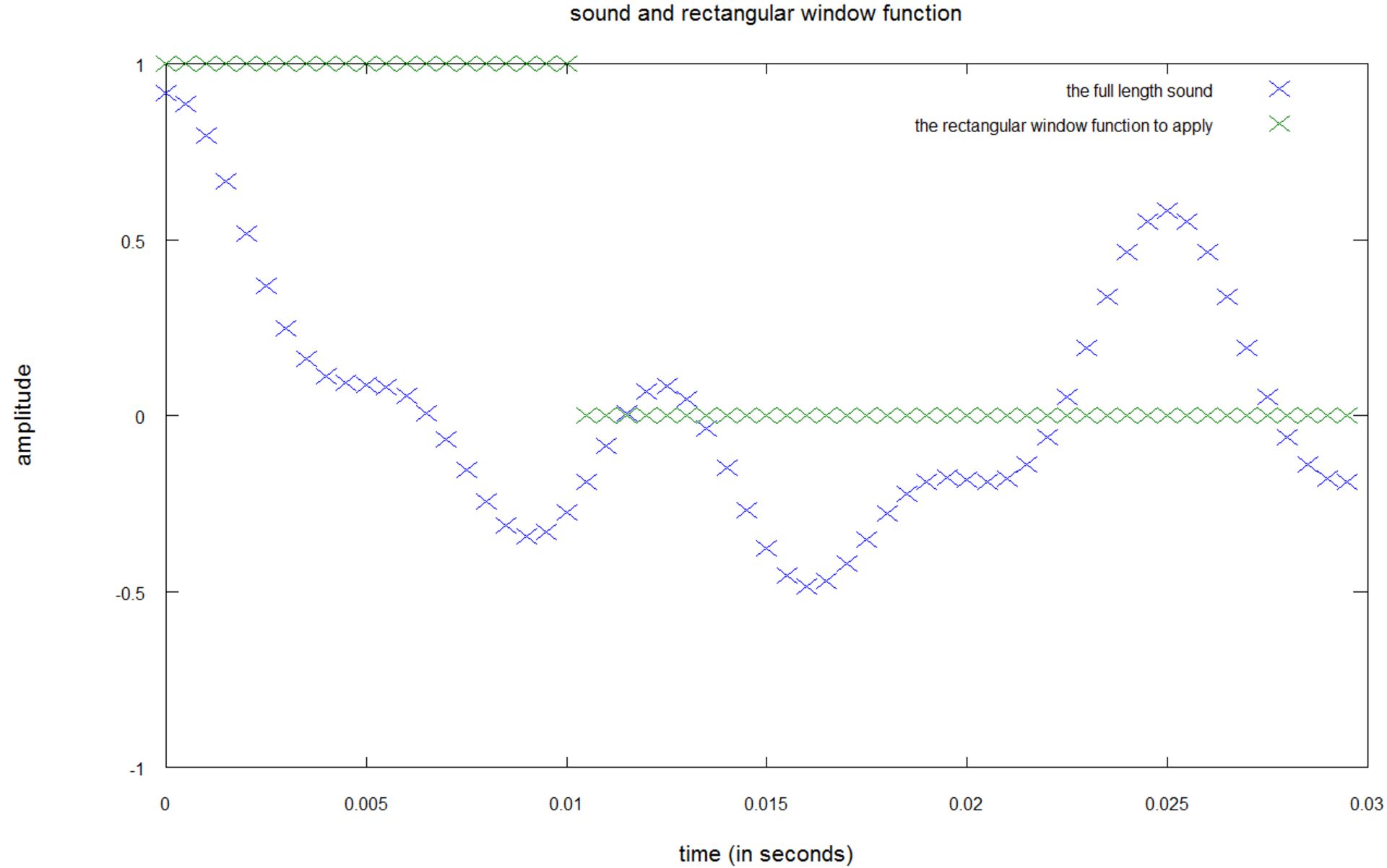
در این نمودار، برای به‌دست آوردن فرکانس‌های بازه‌ی ۰.۱ ثانیه‌ای نخست باید سیگنال صوتی نمونه‌برداری‌شده (رنگ آبی) را در تابع پنجره‌ای (رنگ سبز) ضرب کنید.

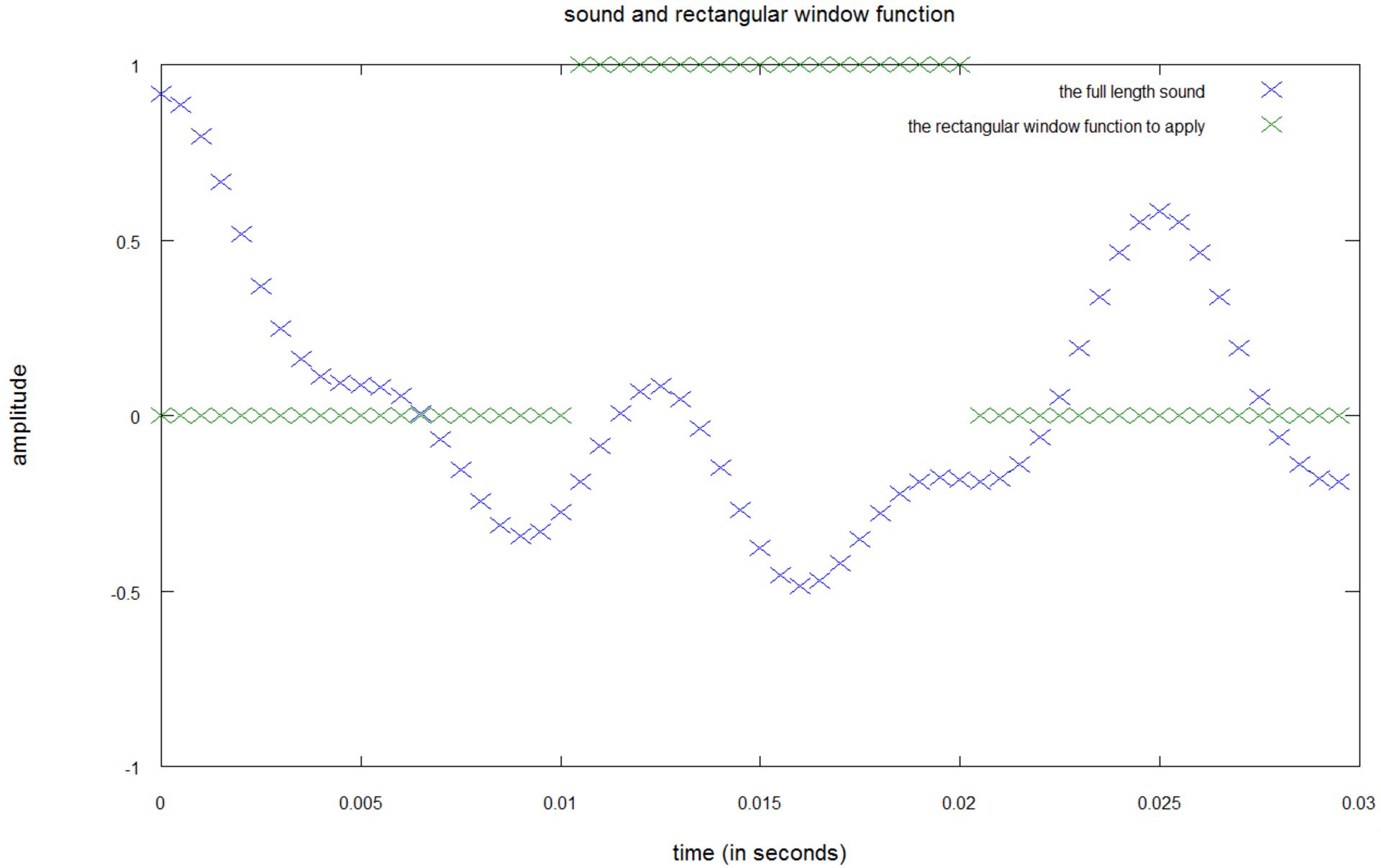
در این نمودار، برای به‌دست آوردن فرکانس‌های بازه‌ی ۰.۱ ثانیه‌ای دوم باید سیگنال صوتی نمونه‌برداری‌شده (رنگ آبی) را در تابع پنجره‌ای (رنگ سبز) ضرب کنید.

با «پنجره‌ای‌سازی» سیگنال صوتی در حقیقت تابع سیگنال صوتی بر حسب زمان را در تابع پنجره‌ای برحسب زمان ضرب می‌کنید. این تابع پنجره‌ای، نشت طیفی را تولید می‌کند. نشت طیفی در حقیقت پدیداری فرکانس‌های جدیدی است که درون سیگنال صوتی وجود ندارند. توان فرکانس‌های واقعی به فرکانس‌های دیگر نشت می‌کند.

در ادامه توضیح ریاضی غیررسمی این پدیده را ارائه می‌کنیم. فرض کنید که بخشی از کل سیگنال صوتی را می‌خواهید، در این صورت باید سیگنال صوتی را در تابع پنجره‌ای ضرب کنید که تنها به بخش مورد نظر شما اجازه‌ی عبور می‌دهد.

part_of_audio(t) = full_audio(t) . window (t)

هنگامی که به‌دنبال فرکانس‌های این بخش از سیگنال صوتی هستید، تبدیل فوریه را روی آن پیاده می‌کنید:

Fourier(part_of_audio(t)) = Fourier(full_audio(t) . window (t))

براساس قضیه‌ی کانوولوشن (* نشان‌دهنده‌ی عملگر کانوولوشن و . نشان‌دهنده‌ی عملگر ضرب است):

Fourier(full_audio(t) . window (t)) = Fourier(full_audio(t))  *  Fourier(window (t))Fourier(part_of_audio(t)) = Fourier(full_audio(t))  *  Fourier(window (t))

* فرکانس part_of_audio(t) به نوع تابع پنجره‌ای window() استفاده شده بستگی دارد.

بحث در رابطه با قضیه‌ی کانوولوشن و نتیجه‌ی پیاده‌سازی آن روی تبدیل فوریه‌ی سیگنال صوتی را در این بخش خاتمه می‌دهیم؛ زیرا وارد شدن به آن، ریاضیات پیشرفته‌ای را می‌طلبد که بی‌شک از حوصله‌ی بحث خارج است. اگر به دنبال کسب اطلاعات بیشتر هستید، توصیه می‌کنیم که با مراجعه به صفحه‌ی ۲۹ در این لینک، اثر ریاضی پیاده‌سازی تابع پنجره‌ای روی یک سیگنال را مشاهده کنید. در این مرحله تنها باید به خاطر داشته باشید که تقسیم سیگنال‌های صوتی به قطعات کوچک برای تحلیل فرکانسی هر قطعه، نشت طیفی را تولید می‌کند.

خاطرنشان می‌کنیم که نمی‌توان از وقوع پدیده‌ی نشت طیفی جلوگیری کرد؛ اما می‌توان با انتخاب تابع پنجره‌ای مناسب، رفتار آن را کنترل کرد: به‌جای استفاده از توابع پنجره‌ای مستطیلی، می‌توانید توابع پنجره‌ای مثلثی، پارزن، بلک‌من یا همینگ را انتخاب کنید...

توابع مستطیلی ساده‌ترین نوع توابع پنجره‌ای محسوب می‌شوند؛ چرا که تنها باید سیگنال‌های صوتی را به قطعات کوچکی تقسیم کنید، اما به‌نظر می‌رسد که برای تحلیل مهم‌ترین فرکانس‌های موجود در یک سیگنال، انتخاب چندان مناسبی نباشد. در ادامه به سه تابع مستطیلی، همینگ و بلک‌من نگاهی خواهیم داشت، برای بررسی تاثیر این سه تابع سیگنال صوتی متشکل از فرکانس‌های زیر را به‌کار خواهیم برد:

• یک فرکانس ۴۰ هرتزی با دامنه‌ی ۲
• یک فرکانس ۱۶۰ هرتزی با دامنه‌ی ۰.۵
• یک فرکانس ۳۲۰ هرتزی با دامنه‌ی ۸
• یک فرکانس ۶۴۰ هرتزی با دامنه‌ی ۱
• یک فرکانس ۱۰۰۰ هرتزی با دامنه‌ی ۱
• یک فرکانس ۱۲۲۵ هرتزی با دامنه‌ی ۰.۲۵
• یک فرکانس ۱۴۰۰ هرتزی با دامنه‌ی ۰.۱۲۵
• یک فرکانس ۲۰۰۰ هرتزی با دامنه‌ی ۰.۱۲۵
• یک فرکانس ۲۵۰۰ هرتزی با دامنه‌ی ۱.۵

در حالت ایده‌آل، تبدیل فوریه‌ی سیگنال یاد‌شده، طیف زیر را تولید خواهد کرد:

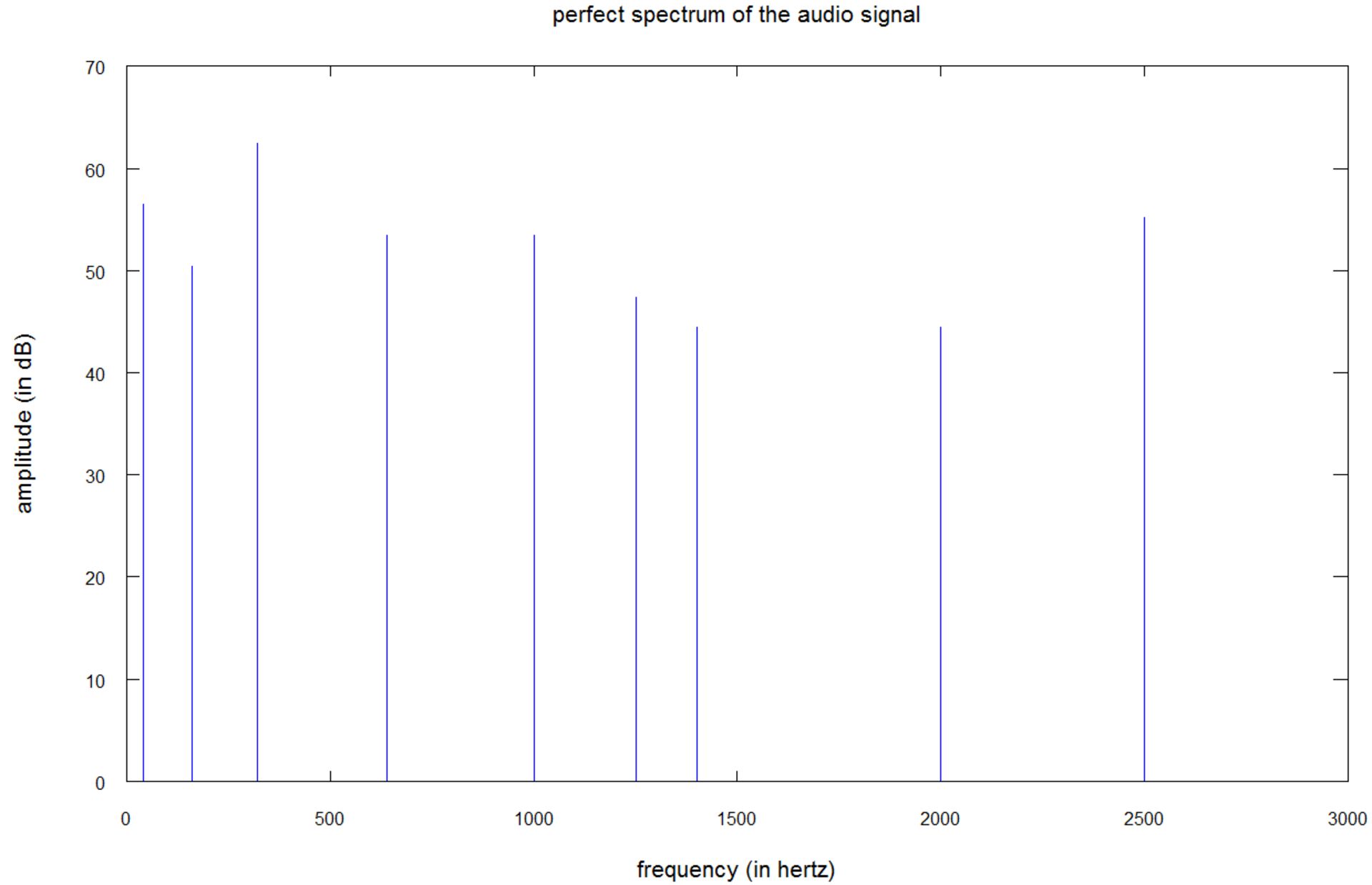
این نمودار، طیفی را با ۹ خط عمودی در فرکانس‌های ۴۰، ۱۶۰، ۳۲۰، ۶۴۰، ۱۰۰۰، ۱۲۲۵، ۱۴۰۰، ۲۰۰۰ و ۲۵۰۰ هرتز را نشان می‌دهد. محور y دامنه‌ی طیفی را برحسب دسی‌بل به تصویر می‌کشد؛ بنابراین مقیاس آن لگاریتمی است. با این مقیاس، صوتی با دامنه‌ی ۶۰ دسی‌بل، ۱۰۰ برابر قدرتمندتر از صوت ۴۰ دسی‌بلی و ۱۰٬۰۰۰ برابر قدرتمندتر از صوت ۲۰ دسی‌بلی است. برای آنکه درک بهتری از موضوع داشته باشید، هنگامی که در یک اتاق ساکت صحبت کنید، شدت صدای شما ۲۰ تا ۳۰ دسی‌بل بیشتر از صدای اتاق در شعاع یک متری‌تان خواهد بود.

برای رسم این نمودار «بی‌نقص»، تبدیل فوریه به یک تابع پنجره‌ای بسیار طولانی ۱۰ ثانیه‌ای اعمال شده است. استفاده از پنجره‌هایی با بازه‌ی زمانی طولانی، نشت طیفی را کاهش می‌دهد؛ اما ۱۰ ثانیه، زمانی طولانی محسوب می‌شود، زیرا در یک قطعه‌ی موسیقی، صدا بسیار سریع‌تر تغییر می‌کند. برای آنکه متوجه تغییرات سریع در موسیقی شوید، از شما دعوت می‌کنیم تا به ویدیو‌های زیر توجه کنید:

• در ویدیوی زیر، صدا در هر ثانیه یک بار تغییر می‌کند، اگرچه این ریتم بسیار آهسته به گوش می‌رسد؛ اما در موسیقی کلاسیک بسیار رایج است.

• در ویدیوی زیر، صدا در هر ثانیه ۲.۷ بار تغییر می‌کند، اگرچه این ریتم بسیار سریع به‌ گوش می‌رسد؛ اما در موسیقی الکترو رایج است.

• در ویدیوی زیر، صدا در هر ثانیه ۸.۳ بار تغییر می‌کند، این ریتم بسیار سریع است؛ اما احتمال دارد که در بخش‌های کوچکی از موسیقی به‌کار رود.

برای آنکه بتوان این تغییرات سریع را ثبت کرد، باید صدا را با استفاده از توابع پنجره به بخش‌های بسیار کوچکی تقسیم کرد. تصور کنید که می‌خواهید فرکانس‌های صدایی را در هر یک‌سوم ثانیه تحلیل کنید.

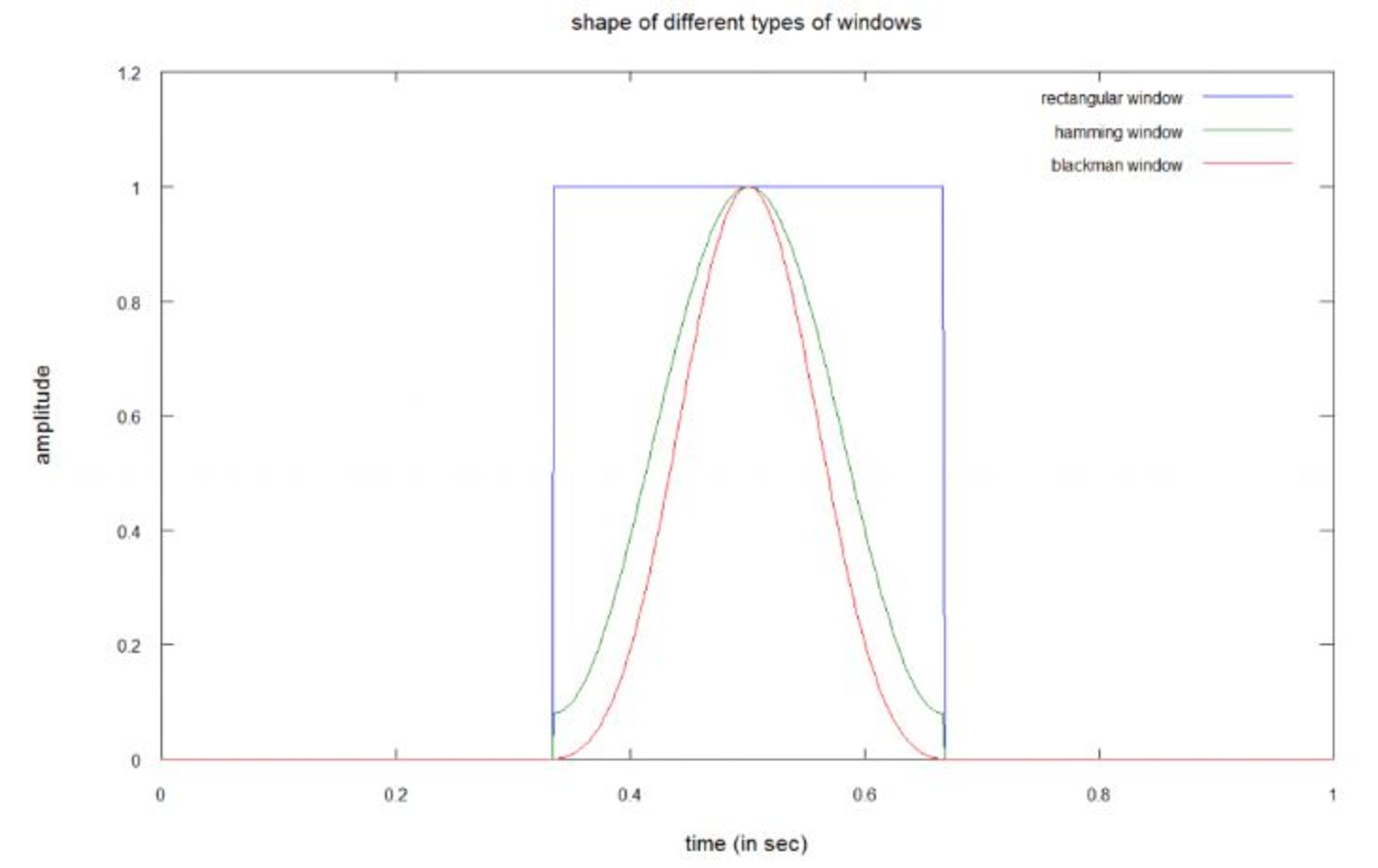
در این نمودار، شما می‌توانید سیگنال صدا را برای به‌دست آوردن سیگنال بین ۰.۳۳۳ و ۰.۶۶۶ ثانیه در یکی از سه نوع تابع پنجره‌ای ضرب کنید. همان‌طور که گفتیم، استفاده از تابع مستطیلی، مانند بریدن سیگنال بین ۰.۳۳۳ ثانیه و ۰.۶۶۶ ثانیه است؛ در حالی برای استفاده از توابع همینگ با بلک‌من باید سیگنال را در سیگنال پنجره‌ای ضرب کنید.

تصویر زیر، طیف صدای قبلی با تابع پنجره‌ای ۴۰۹۶ نمونه‌ای را نشان می‌دهد:

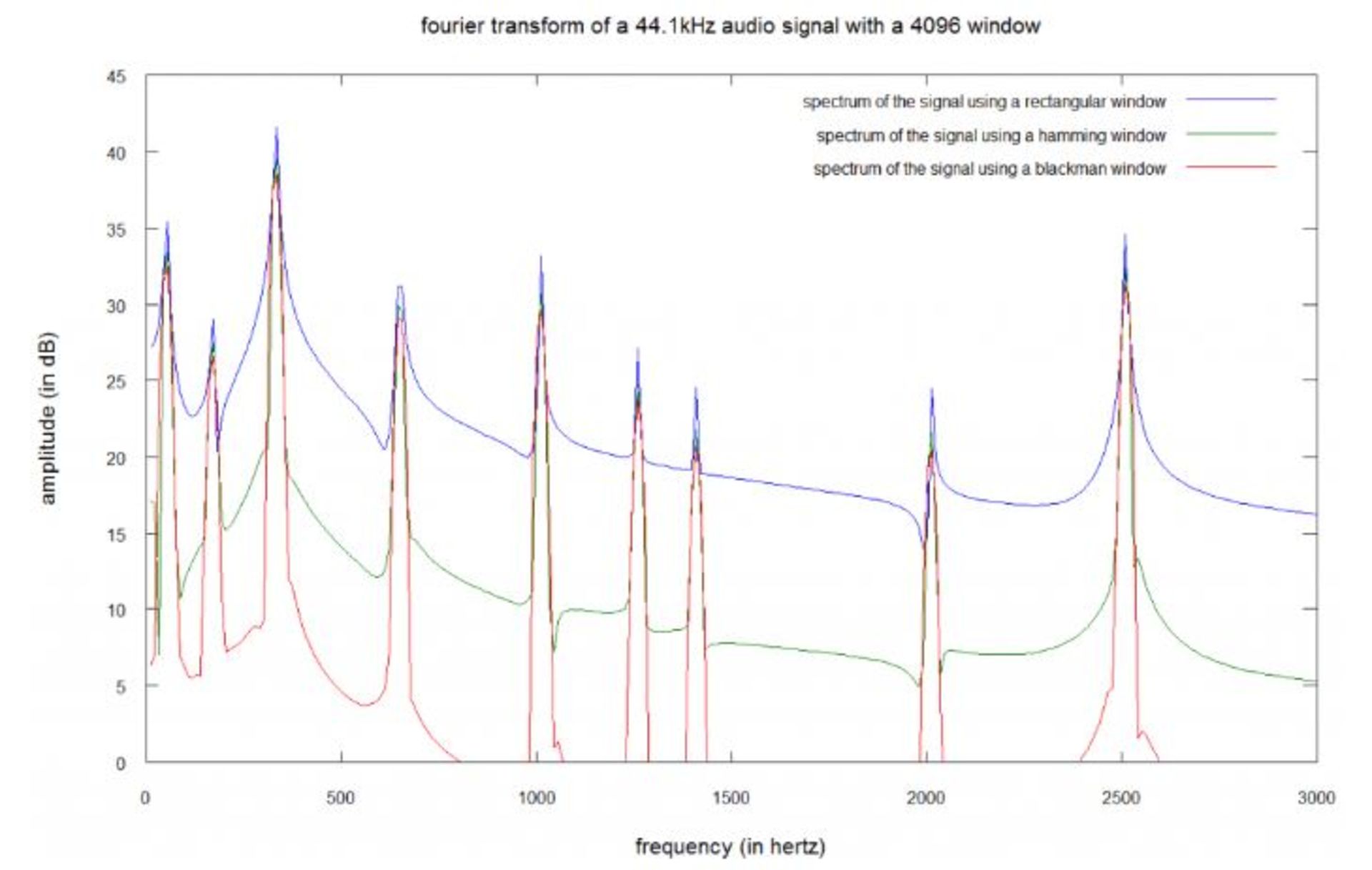
سیگنال با فرکانس ۴۴۱۰۰ هرتزی نمونه‌برداری شده است؛ بنابراین تابع پنجره‌ای ۴۰۹۶ نمونه‌ای، یک بخش ۹۳ میلی‌ثانیه‌ای (۴۴۱۰۰/۴۰۹۶) و وضوح فرکانسی ۱۰.۷ هرتزی را نشان می‌دهد.

این نمودار نشان می‌دهد که تمام توابع پنجره‌ای، طیف حقیقی صدا را تغییر می‌دهند. به‌وضوح می‌توان دید که بخشی از توان فرکانس‌های حقیقی به همسایگی‌ آن‌ها پخش شده است. طیف حاصل از تابع مستطیلی بدترین عملکرد را دارد؛ چرا که نشت طیفی در آن بسیار بیش‌تر از دو تابع دیگر است، این موضوع بین فرکانس‌های ۴۰ تا ۱۶۰ هرتز، بیش از پیش جلوه می‌کند. تابع بلک‌من نزدیک‌ترین طیف را به نمونه‌ی حقیقی تولید می‌کند.

نمودار زیر، نمونه‌ای دیگری را با تبدیل فوریه‌ی مبتنی بر تابع پنجره‌ای ۱۰۲۴ نمونه‌ای نشان می‌دهد:

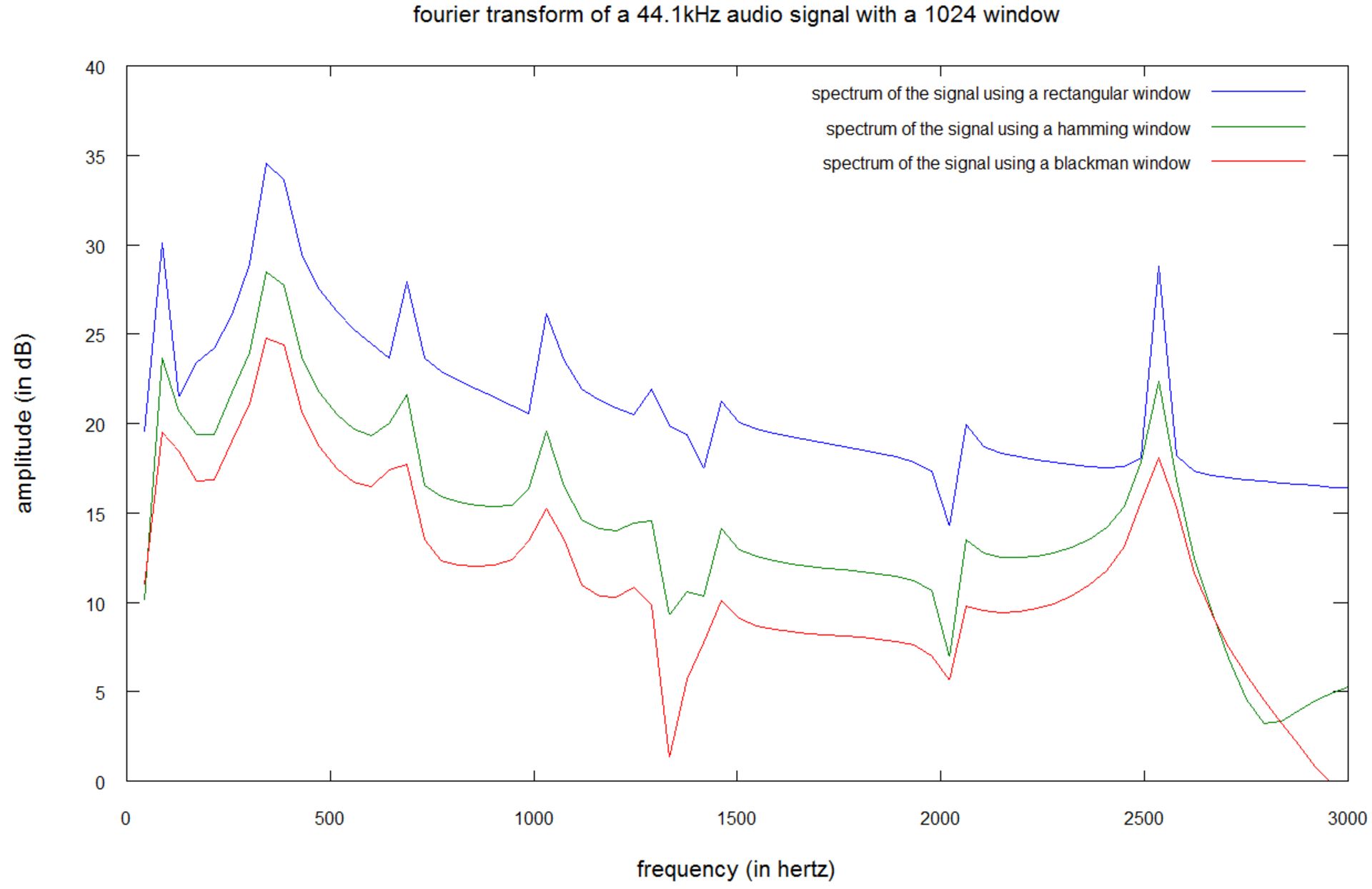
سیگنال با فرکانس ۴۴۱۰۰ هرتزی نمونه‌برداری شده است؛ بنابراین تابع پنجره‌ای ۱۰۲۴ نمونه‌ای، یک بخش ۲۳ میلی‌ثانیه‌ای (۴۴۱۰۰/۱۰۲۴) و وضوح فرکانسی ۴۳ هرتزی را نشان می‌دهد.

این بار، تابع مستطیلی، بهترین طیف را تولید می‌کند. در هر سه تابع پنجره‌ای، فرکانس ۱۶۰ هرتزی توسط نشت طیفی تولید‌شده با فرکانس‌های ۴۰ و ۳۲۰ هرتزی پنهان شده است. تابع بلک‌من بدترین نتیجه را تولید می‌کند؛ چرا که فرکانس ۱۲۲۵ هرتزی نزدیک به ناپدید شدن است.

مقایسه‌ی دو نمودار نشان می‌دهد که نشت طیفی در تمام توابع پنجره‌ای با بالا رفتن وضوح فرکانسی، افزایش پیدا می‌کند. الگوریت هویت‌سنجی صوتی شزم، به‌دنبال بلندترین فرکانس درون قطعه‌ی موسیقی می‌گردد؛ اما به‌دلیل نشت طیفی، نمی‌توان به‌سادگی بالاترین فرکانس را به‌دست آورد. در نمونه‌ی آخر، سه فرکانس بلند تقریبی، ۳۲۰، ۲۷۷ (۴۳-۳۲۰) و ۳۶۳ (۴۳+۳۲۰) هرتز هستند؛ اما تنها فرکانس ۳۲۰ هرتز وجود دارد.

بهترین یا بدترین تابع پنجره‌ای وجود ندارد. هر تابع پنجره‌ای، ویژگی‌های منحصربه‌فردی دارد و بسته به نوع مسئله می‌توان نوع خاصی را برگزید. تابع مستطیلی به‌لحاظ وضوح بهترین گزینه‌ برای سیگنال‌های سینوسی با توان‌های نزدیک به هم محسوب می‌شود؛ اما این نوع تابع برای سیگنال‌های سینوسی با دامنه‌های بسیار متفاوت (مانند آنچه در موسیقی رخ می‌دهد؛ چرا که نت‌های موسیقی بلندی یکسانی ندارند)، انتخاب بسیاری بدی به‌شمار می‌رود.

توابعی نظیر بلک‌من برای جلوگیری از ناپدید شدن فرکانس‌های ضعیف توسط فرکانس‌های قدرتمند به‌موجب نشت طیفی، انتخاب بهتری هستند؛ اما این توابع در خصوص نویز عملکرد بدی دارند؛ چرا که وجود نویز باعث ناپدید شدن فرکانس‌های بیشتری نسبت به تابع مستطیلی می‌شود. این موضوع برای الگوریتمی مانند شزم که باید توان مواجهه با نویز را داشته باشد، مشکل‌ساز خواهد بود (به‌عنوان مثال هنگامی که در یک محیط شلوغ به‌‌دنبال شناسایی موسیقی خاصی با شزم هستید، نویز بسیاری وجود خواهد داشت).

تابع همینگ بین دو تابع مستطیلی و بلک‌من قرار می‌گیرد و از این رو به‌نظر می‌رسد که گزینه‌ای بهتری برای الگوریتمی نظیر شزم باشد. در پایان این بخش توصیه می‌کنیم که برای به‌دست آوردن اطلاعات بیشتری در رابطه با توابع پنجره‌ای و نشت طیفی به منابع زیر مراجعه کنید:

• منبع اول
• منبع دوم
• منبع سوم

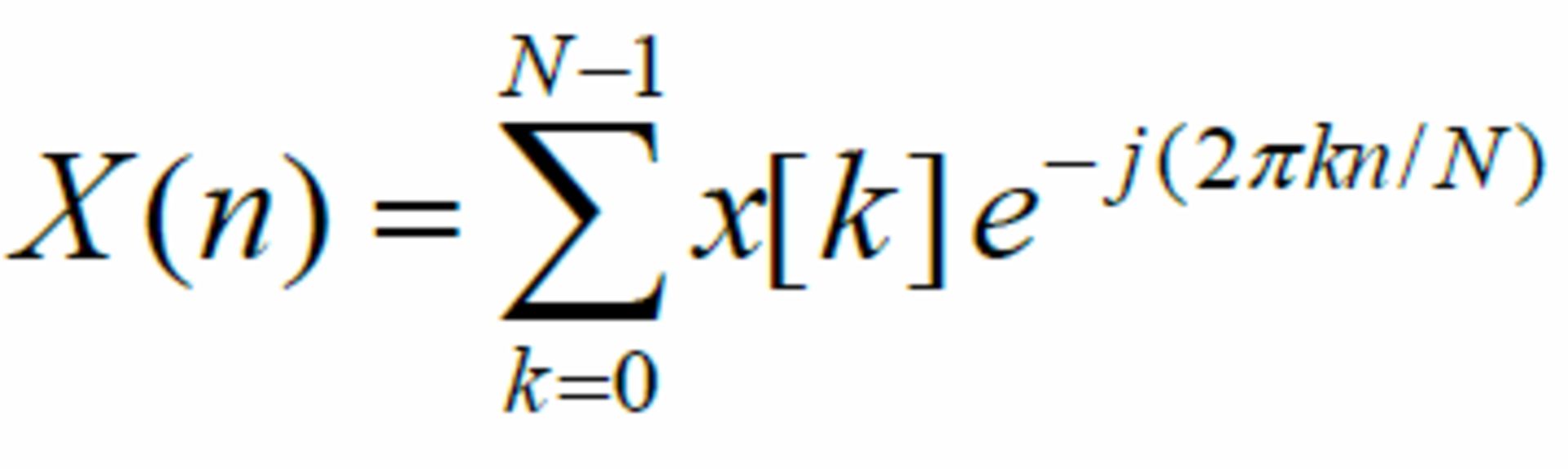
اگر بار دیگر به رابطه‌ی به رابطه‌ی DFT توجه کنید، مشاهده خواهید کرد که برای محاسبه‌ی یک بازه، باید N جمع و N ضرب را انجام دهید که در آن‌ها N ابعاد پنجره محسوب می‌شود؛ بدین ترتیب به‌دست آوردن N بازه، مستلزم انجام ۲ در N به‌توان ۲ محاسبه است که تعداد بسیار زیادی به‌شمار می‌رود.

به‌عنوان مثال، یک قطعه‌ی موسیقی سه دقیقه‌ای با فرکانس ۴۴.۱ کیلوهرتزی را تصور کنید که باید طیف‌نگاره‌ی آن را با تابع پنجره‌ای ۴۰۹۶ نمونه‌ای محاسبه کنید؛ بدین ترتیب باید ۱۰.۷ یا (۴۴۱۰۰/۴۰۹۶) DFT به‌ازای هر ثانیه را به‌دست آورید؛ بنابراین کل قطعه‌ی موسیقی ۱۹۳۸ نمونه DFT خواهد داشت. هر DFT به انجام ۱۰۷ × ۳.۳۵ عملیات (۴۰۹۶۲ × ۲) نیاز خواهد داشت؛ از این رو محاسبه‌ی طیف‌نگاره‌ی کل قطعه‌ی موسیقی، مستلزم انجام ۱۰۱۰ × ۶.۵ عملیات ریاضی خواهد بود.

فرض می‌کنیم که کلکسیونی از ۱۰۰۰ قطعه‌ی موسیقی سه دقیقه‌ای را در اختیار دارید؛ برای به‌دست آوردن طیف‌نگاره‌ی کل این قطعات موسیقی باید ۱۰۱۳ × ۶.۵ عملیات ریاضی را انجام دهید، انجام این محاسبات حتی با داشتن پردازنده‌ای قدرتمند، چندین روز / ماه به‌طول خواهد انجامید.

خوشبختانه نسخه‌ی سریع‌تری از DFT با نام FFT یا تبدیل سریع فوریه وجود دارد. برخی از نسخه‌های DFT تنها به انجام ۱.۵ × N × log(N) عملیات ریاضی نیاز دارند. استفاده از FFT به‌جای DFT برای کلکسیون موسیقی یادشده در پاراگراف قبلی به ۳۴۰ برابر محاسبات کمتری (۱۰۱۱ × ۱.۴۳) نیاز خواهد داشت و برای انجام آن به چند دقیقه / ساعت نیاز خواهید داشت.

این مثال، مصالحه‌ای دیگری را نیز نشان می‌دهد: اگرچه افزایش ابعاد پنجره، وضوح فرکانسی را بهبود می‌بخشد؛ مدت‌زمان لازم برای انجام محاسبات را نیز افزایش می‌دهد. به‌عنوان مثال چنانچه طیف‌نگاره‌ی کلکسیون موسیقی یادشده را با استفاده از پنجره‌ی ۵۱۲ نمونه‌ای محاسبه کنید (وضوح فرکانسی ۸۶ هرتزی)، می‌توان با استفاده از تبدیل سریع فوریه، نتیجه را طی ۱۰۱۱ × ۱.۰۷ محاسبه به‌دست آورد که به‌صورت تقریبی یک‌چهارم برابر سریع‌تر از حالت انجام محاسبه با پنجره‌ی ۴۰۹۶ نمونه‌ای (وضوح فرکانسی ۱۰.۷۷ هرتزی) است.

این پیچیدگی زمانی از آنجایی حائز اهمیت است که هنگام شناسایی یک قطعه‌ی موسیقی با استفاده از شزم، گوشی شما باید طیف‌نگاره‌ی صوت ضبط‌شده را محاسبه کند؛ در حالی که پردازنده‌های موبایل بسیار ضعیف‌تر از پردازنده‌های دسکتاپ هستند.

خوشبختانه راهکاری موسوم به نمونه‌کاهی وجود دارد که به‌موجب آن می‌توان در آنِ واحد، ضمن حفظ وضوح فرکانسی، ابعاد پنجره را نیز کاهش داد. یک قطعه‌ی موسیقی با فرکانس ۴۴۱۰۰ هرتزی را در نظر می‌گیریم، چنانچه این قطعه را فرکانس ۱۱۰۲۵ هرتز (۴/۴۴۱۰۰) مجددا نمونه‌برداری کنید، چه با انجام تبدیل سریع فوریه روی یک قطعه‌ی موسیقی ۴۴.۱ کیلوهرتزی با پنجره‌ی ۴۰۹۶ نمونه‌ای و چه با محاسبه‌ی تبدیل سریع فوریه روی یک قطعه با نمونه‌برداری مجدد ۱۱ کیلوهرتزی و تابع پنجره‌ای ۱۰۲۴ نمونه‌ای، به وضوح فرکانسی یکسانی دست خواهید یافت. تنها تفاوت این است که موسیقی با نمونه‌برداری مجدد تنها فرکانس‌ها صفر تا ۵ کیلوهرتزی را در بر خواهد داشت؛ اما مهم‌ترین بخش موسیقی بین فرکانس‌های یادشده قرار دارد. در حقیقت، بسیاری از افراد بین موسیقی ۱۱ کیلوهرتزی و موسیقی ۴۴.۱ کیلوهرتزی، تفاوتی متوجه نخواهند شد؛ بنابراین مهم‌ترین فرکانس‌ها کماکان در موسیقی با نمونه‌برداری مجدد موجود هستند و این موضوع برای الگوریتمی مانند شزم بسیار حائز اهمیت است.

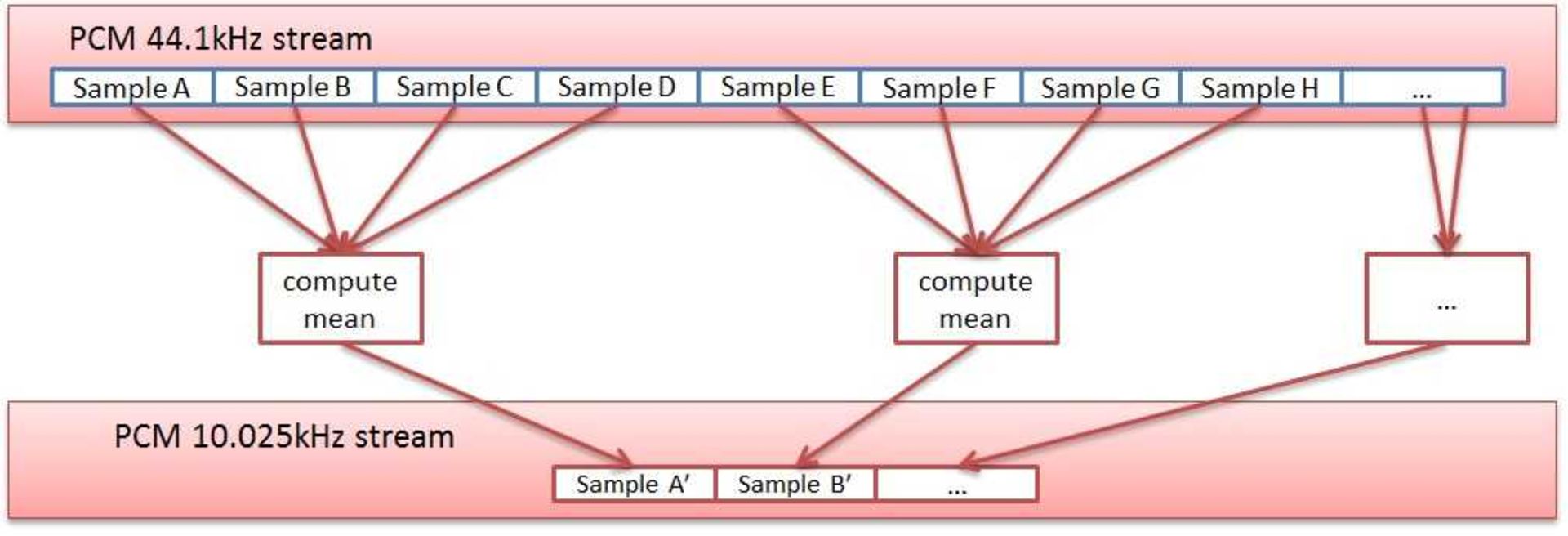
نمونه‌کاهی یک قطعه‌ی موسیقی ۴۴.۱ کیلوهرتزی به نمونه‌ی ۱۱.۰۲۵ کیلوهرتزی چندان دشوار نیست: یکی از راهکارهای ساده برای نمونه‌کاهی، نمونه‌برداری با گروه‌های چهارتایی و تبدیل این گروه به یک نمونه از طریق میانگین‌گیری بین چهار نمونه است؛ اما در این بین باید برای جلوگیری از Aliasing‌، پیش از نمونه‌کاهی، فرکانس‌های بالا را فیلتر کرد. این فرآیند با استفاده از فیلتر دیجیتال پایین‌گذر امکان‌پذیر است.

مجددا به بحث تبدیل سریع فوریه باز‌می‌گردیم؛ ساده‌ترین نسخه از FFT الگوریتم کولی – توکی با مبنای ۲ است. در الگوریتم یادشده به‌جای محاسبه‌ی مستقیم تبدیل فوریه روی N نمونه‌ی پنجره:

• پنجره‌ی N نمونه‌ای به دو پنجره‌ی N/2 نمونه‌ای تقسیم می‌‌شود
• تبدیل سریع فوریه به‌صورت بازگشتی برای ۲ پنجره‌ی N/2 نمونه‌ای محاسبه می‌کند
• تبدیل سریع فوریه به‌صورت بهینه برای پنجره‌ی N‌ نمونه‌ای از دو FFT پیشین به‌دست می‌آید

بخش پایانی صرفا با انجام N عملیات توسط یک ترفند ریاضی روی ریشه‌ی واحد (عبارت نمایی) صورت می‌گیرد. کُد زیر در زبان پایتون و برای محاسبه‌ی تبدیل سریع فوریه نوشته شده است. برای کسب اطلاعات بیشتر درباره‌ی تبدیل سریع فوریه می‌توانید به این مقاله‌ی ویکیپدیا مراجعه کنید.

from cmath import *def fft(x): N=len(x) if N==1: return x even=fft([x[k] for k in range(0,N,2)]) odd= fft([x[k] for k in range(1,N,2)]) M=N/2 l=[ even[k] + exp(-2j*pi*k/N)*odd[k] for k in range(M) ] r=[ even[k] - exp(-2j*pi*k/N)*odd[k] for k in range(M) ] return l+r

در بخش‌‌هایی پیشین با مباحث بسیاری آشنا شدیم؛ اما اکنون زمان آن رسیده است تا با کنار هم قرار دادن مباحث یادشده، متوجه شویم که چگونه شزم به‌سرعت موسیقی را شناسایی می‌کند. در ابتدا نگاهی کلی به شزم خواهیم داشت، سپس به‌چگونگی تولید هویت صوتی می‌پردازیم و در نهایت با مکانیزم جست‌وجوی صوتی بهینه این بخش را به پایان خواهیم برد.

یادداشت: از این مرحله به بعد، با این فرض پیش خواهیم کرد که شما بخش‌های مربوط به نت‌های موسیقی، تبدیل سریع فوریه و توابع پنجره‌ای را مطالعه کرده‌اید. در بخش حاضر گاهی از واژه‌های «فرکانس»، «بازه»، «نت» یا «بازه‌ی فرکانسی» اشاره خواهیم کرد که همگی مفهوم یکسانی را می‌رسانند؛ زیرا ما با سیگنال‌های صوتی دیجیتال سروکار داریم.

هویت صوتی، خلاصه‌ای دیجیتال است که از آن می‌توان برای شناسایی یک نمونه‌ی صوتی یا شناسایی نمونه‌های مشابه در یک پایگاه داده‌ی صوتی استفاده کرد؛ به‌عنوان مثال هنگامی که شما موسیقی خاصی را برای شخصی زمزمه می‌کنید، در حقیقت در حال ایجاد یک هویت صوتی هستید؛ چرا که بخش‌هایی از موسیقی را از ذهن خود استخراج می‌کنید که از نظر شما ضروری هستند و اگر شما خواننده‌ی خوبی نیز باشید؛ شنونده قطعه‌ی موسیقی را شناسایی خواهد کرد.

پیش از اینکه وارد جزئیات شویم، در تصویر زیر می‌توانید تصویری از ساختار ساده‌‌شده‌ی احتمالی شزم را مشاهده کنید؛ به یاد داشته باشید که این تصویر صرفا براساس حدسیات و برمبنای مقاله‌ای است که در سال ۲۰۱۳ توسط یکی از بنیان‌گذاران شزم منتشر شد.

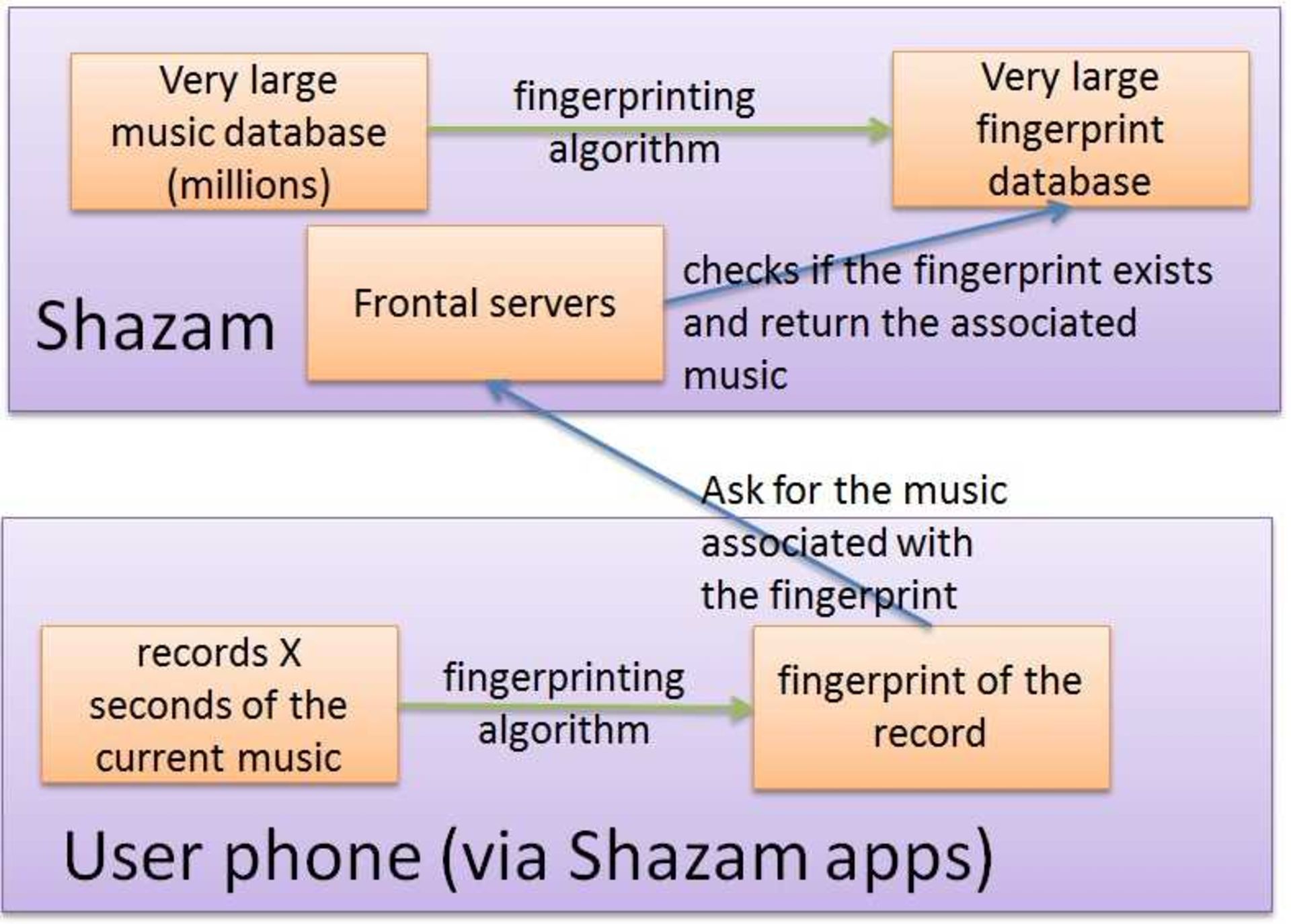
در سمت سرور:

• شزم هویت‌ها را از دیتابیس بسیار گسترده‌ای از قطعات موسیقی از پیش محاسبه می‌کند
• تمام این هویت‌های ایجادشده درون یک دیتابیس هویت قرار می‌گیرند که هربار پس از اضافه‌شدن یک قطعه‌ی موسیقی به دیتابیس شزم، به‌روز می‌شود

در سمت کلاینت:

• هنگامی که کاربری از اپلیکیشن شزم استفاده می‌کند، این اپلیکیشن در ابتدا از طریق میکروفون گوشی، بخشی از موسیقی در حال پخش را ضبط می‌کند
• گوشی همان الگوریتم ایجاد هویت اجراشده توسط شزم را حین ضبط پیاده می‌کند
• گوشی هویت ایجادشده را به شزم ارسال می‌کند
• شزم هویت دریافتی را دیتابیس خود مطابقت می‌دهد، چنانچه این فرآیند شکست خورد، به کاربر اعلام می‌کند که موسیقی را شناسایی نکرد و چنانچه موفق شد، به‌دنبال متاداده‌های مربوط به هویت دریافتی، نظیر نام قطعه، لینک آیتونز، لینک آمازون ... می‌گردد و نتیجه را به کاربر ارائه می‌دهد

نکات کلیدی مربوط به شزم عبارت هستند از:

• مقاومت در برابر نویز / نقص: چرا که موسیقی ضبط‌شده توسط یک گوشی در محیط‌های بیرونی، اغلب اوقات کیفیت پایینی دارند؛ استفاده از تابع پنجره‌ای، آثاری را از خود به‌جای می‌گذارد؛ میکروفون ضعیف موجود در گوشی‌های هوشمند، نویز و اعوجاج بسیاری تولید می‌کند و دلایل فیزیکی گوناگون دیگر
• هویت‌ها باید مستقل از زمان باشند: هویت یک قطعه‌ی موسیقی کامل باید با تنها یک بخش ۱۰ ثانیه‌ای از موسیقی مطابقت داشته باشد
• تطبیق هویت باید سریع باشد: چه کسی می‌تواند چندین دقیقه / ساعت در انتظار گرفتن پاسخی از شزم باشد؟
• تعداد نتایج مثبت کاذب (False Positive) پایین باشد: چه کسی می‌خواهد پاسخی دریافت کند که با موسیقی صحیح هم‌خوانی ندارد

هویت‌های صوتی با هویت‌های کامپیوتری نظیر SSHA یا MD5 متفاوت هستند؛ چرا که دو فایل متفاوت به‌لحاظ تعداد بیت که موسیقی یکسانی را در بر دارند، باید هویت صوتی یکسانی داشته باشند؛ به‌عنوان مثال یک قطعه‌ی موسیقی با فرمت 256kbit ACC آیتونز باید هویت یکسانی با همان موسیقی در فرمت 256kbit MP3 آمازون یا 128kbit WMA مایکروسافت تولید کند، برای حل این مشکل، الگوریتم‌های ایجاد هویت موسیقی از طیف‌نگاره‌ی سیگنال‌های صوتی برای استخراج هویت آن‌ها بهره می‌برند.

همان‌طور که پیش‌تر گفتیم، برای تولید طیف‌نگاره‌ی یک صوت دیجیتال باید تبدیل سریع فوریه را روی آن اِعمال کنیم. در یک الگوریتم ایجاد هویت صوتی به وضوح فرکانسی مناسبی نیاز داریم (به‌عنوان مثال ۱۰.۷ هرتز) تا بدین ترتیب نشت طیفی را کاهش دهیم و از نت‌های نواخته‌شده درون قطعه‌ی موسیقی شناخت خوبی داشته باشیم. همچنین باید زمان محاسبه را تا جایی که ممکن است کاهش دهیم و این موضوع مستلزم استفاده از پنجره‌ای با ابعاد کوچک است. در مقاله‌ی پژوهشی شزم توضیحی درباره‌ی چگونگی به‌دست‌ آوردن طیف‌نگاره نیامده است؛ اما احتمالا راهکار آن‌ها بدین شکل باشد:

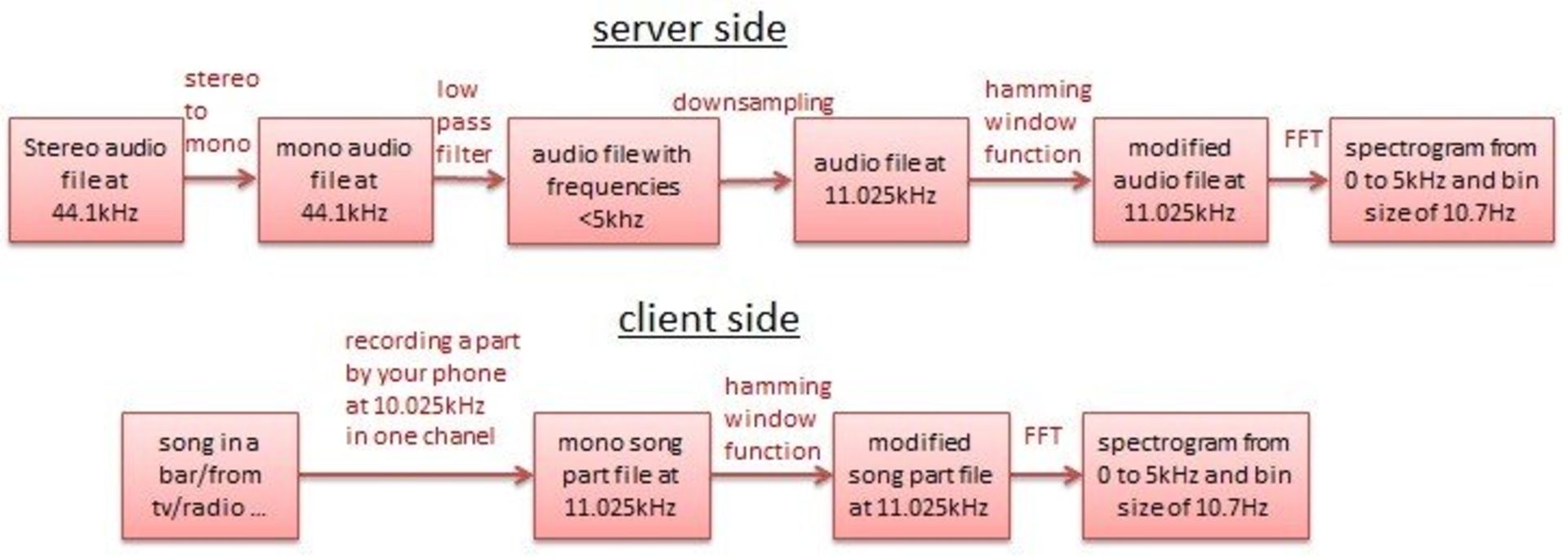
در سمت سرور (شزم)، صوت ۴۴.۱ کیلوهرتزی (از CD، MP3 یا هر فرمت صوتی دیگری) باید از فیلتر مبدل استریو به مونو گذر کند؛ برای انجام این کار می‌توان از اسپیکر سمت چپ و راست میانگین گرفت. پیش از نمونه‌کاهی برای جلوگیری از وقوع پدیده‌ی Aliasing، باید فرکانس‌های بالاتر از ۵ کیلوهرتز را فیلتر کرد، سپس صدا با نرخ ۱۱.۰۲۵ کیلوهرتز نمونه‌برداری می‌شود.

در سمت کلاینت (گوشی)، نرخ‌ نمونه‌برداری میکروفونی که صدا را ضبط می‌کند، باید ۱۱.۰۲۵ کیلوهرتز باشد. سپس در هر دو مورد، باید تابعی پنجره‌ای را روی سیگنال پیاده کرد؛ به‌عنوان مثال تابع ۱۰۲۴ نمونه‌ای همینگ، شما می‌توانید دلیل انتخاب چنین تابعی را در فصل توابع پنجره‌ای بیابید. در نهایت تبدیل سریع فوریه روی تمام ۱۰۲۴ نمونه اِعمال می‌شود. با انجام این کار، هر کدام از تبدیل‌های سریع فوریه، ۰.۱ ثانیه از موسیقی را آنالیز می‌کند و بدین ترتیب طیف‌نگاره‌ای ایجاد می‌شود:

• از صفر تا ۵۰۰۰ هرتز
• با بازه‌ی فرکانسی ۱۰.۷ هرتزی
• ۵۱۲ فرکانس محتمل
• واحد زمانی ۰.۱ ثانیه‌ای

در این مرحله طیف‌نگاره‌ی موسیقی را در اختیار داریم. از آنجایی که شزم باید در برابر نویز مقاوم باشد، تنها بلند‌ترین نت‌ها حفظ می‌شوند؛ اما به‌ دلایل زیر نمی‌توان صرفا در هر ۰.۱ ثانیه قدرتمندترین فرکانس‌ها را حفظ کرد:

• در ابتدای مقاله درباره‌ی مدل‌های سایکوآکوستیک صحبت کردیم. گوش انسان در شنیدن صداهای آرام (کمتر از ۵۰۰ هرتز) بیش از صداهای میانی (۵۰۰ تا ۲۰۰۰ هرتز) یا صداهای بلند (بیش از ۲۰۰۰ هرتز)، دچار مشکل می‌شود؛ از این رو، صداهای آرام بسیاری از قطعات موسیقی، پیش از انتشار، به‌صورت مصنوعی، افزایش داده می‌شوند. اگر تنها قدرتمندترین فرکانس‌ها را انتخاب کنید، در نهایت تنها صداهای آرام را در اختیار خواهید داشت و اگر دو قطعه‌ی موسیقی، ریتم درام یکسانی داشته باشند، ممکن است طیف‌نگاره‌ی فیلتر‌شده‌ی آن‌ها بسیار نزدیک به یکدیگر باشد، در حالی که یکی از قطعات از فلوت استفاده می‌کند و دیگری از گیتار بهره می‌برد.
• در بخش مربوط به توابع پنجره‌ای دیدیم که به‌دلیل نشت طیفی در مجاورت فرکانس‌های بسیار قدرتمند، فرکانس‌های قدرتمند دیگری در طیف‌نگاره ظاهر خواهند شد که وجود خارجی ندارند؛ بنابراین باید قادر به انتخاب نمونه‌ی حقیقی باشید.

در ادامه راهکار ساده‌ای را شرح می‌دهیم که به موجب آن می‌توان تنها فرکانس‌های قدرتمند را انتخاب کرد و مشکلات پیشین را کاهش داد:

گام اول – برای هر نتیجه‌ی تبدیل سریع فوریه، ۵۱۲ بازه را درون ۶ باند لگاریتمی قرار می‌دهیم:

• باندی با صدای بسیار پایین (بازه‌ی صفر تا ۱۰)
• باندی با صدای پایین (بازه‌ی ۱۰ تا ۲۰)
• باندی با صدای پایین – میانی (بازه‌ی ۲۰ تا ۴۰)
• باندی با صدای میانی (بازه‌ی ۴۰ تا ۸۰)
• باندی با صدای میانی – بالا (بازه‌ی ۸۰ تا ۱۶۰)
• باندی با صدای بسیار بالا (بازه‌ی ۱۶۰ تا ۵۱۱)

گام دوم – برای هر باند، قدرتمندترین بازه‌ی فرکانسی را حفظ می‌کنیم

گام سوم – مقدار میانگین این ۶ بازه‌ی قدرتمند را محاسبه می‌کنیم

گام چهارم – بازه‌هایی را بالاتر از مقدار میانگین هستند، حفظ می‌کنیم

گام چهارم بسیار حائز اهمیت است؛ چرا که ممکن است:

• یک قطعه‌ی موسیقی آکاپلا (بدون همراهی آلات موسیقی) به همراه خواننده‌های سوپرانو (صدای بسیار بم) با فرکانس‌های میانی یا میانی – بالا
• یک قطعه‌ی موسیقی جاز / رپ با تنها فرکانس‌های پایین یا پایین – میانی
• ...

داشته باشیم.

و نباید فرکانس ضعیفی را صرفا به‌خاطر آن نگه داشت که داخل باند خود، قوی‌ترین است؛ اما این الگوریتم یک محدودیت دارد؛ در بسیاری از قطعات موسیقی، برخی از بخش‌ها بسیار آرام هستند (مانند ابتدا یا پایان یک قطعه)؛ چنانچه این بخش‌ها را آنالیز کنیم، فرکانس‌های بالای کاذبی را به‌دست خواهیم آورد؛ چرا که مقدار میانگین این بخش‌ها بسیار پایین است. برای جلوگیری از چنین مساله‌ای، به‌جای محاسبه‌ی میانگین ۶ بازه‌ی قدرتمند از تبدیل سریع فوریه‌ی فعلی (تبدیلی که ۰.۱ ثانیه از قطعه‌ی موسیقی را نشان می‌دهد)، می‌توان میانگین قدرتمندترین بازه‌های کل قطعه‌ی موسیقی را محاسبه کرد.

به‌صورت خلاصه، با پیاده‌سازی این الگوریتم، طیف‌نگاره‌ی موسیقی را فیلتر می‌کنیم تا بدین ترتیب بالاترین سطح انرژی طیف را که بلندترین نت‌ها را نشان می‌دهد، حفظ کنیم. برای آنکه به‌صورت شهودی متوجه ماهیت فیلترینگ شوید، در تصویر زیر می‌توانید طیف‌نگاره‌ی حقیقی یک قطعه‌ی موسیقی ۱۴ ثانیه‌ای را مشاهده کنید.

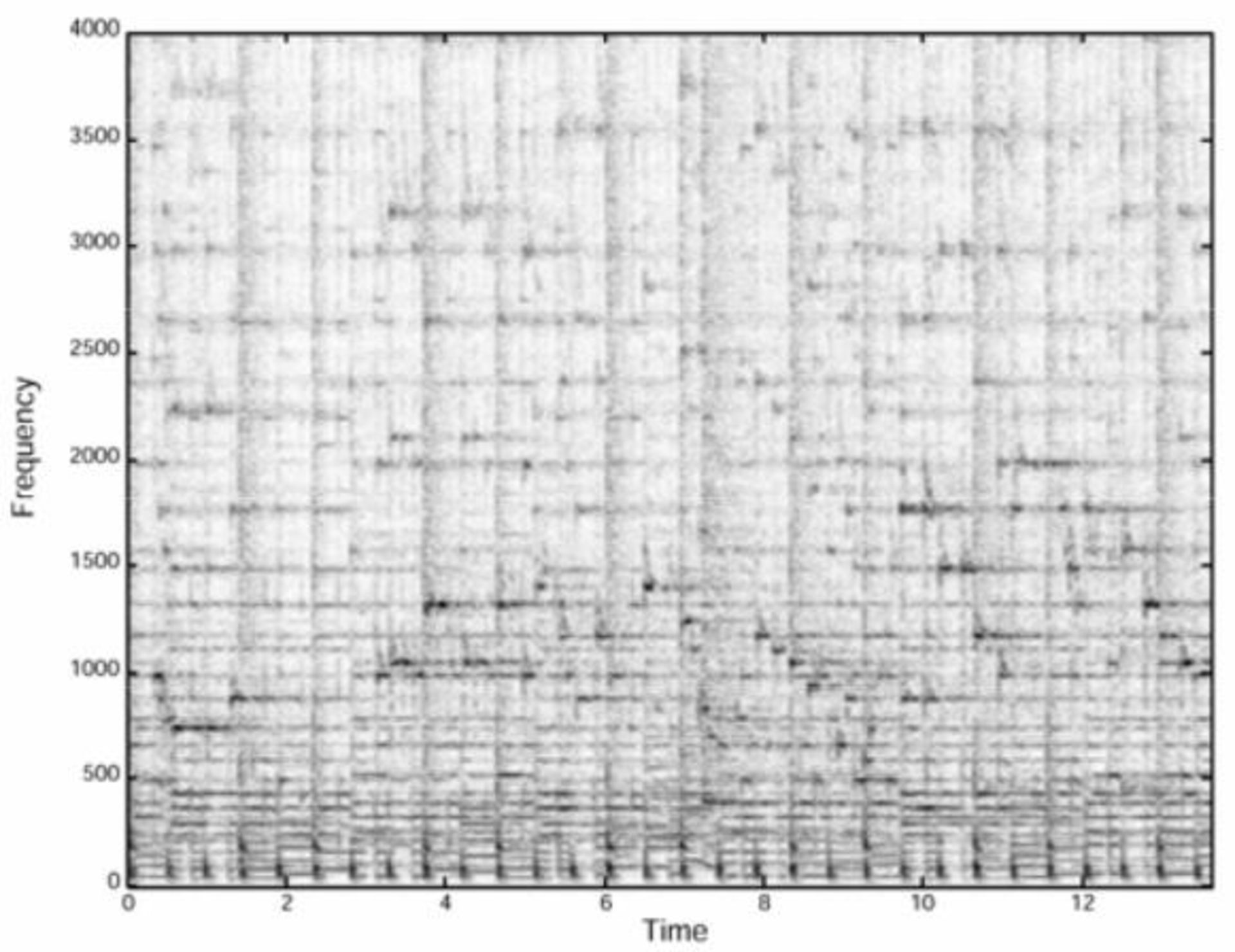
نمودار بالا در مقاله‌ی پژوهشی شزم آمده است. در این طیف‌نگاره می‌توانید فرکانس‌هایی را مشاهده کنید که بسیار قدرتمندتر از نمونه‌های دیگر هستند. چنانچه الگوریتم پیشین را روی طیف‌نگاره پیاده کنید، به چنین تصویری خواهید رسید:

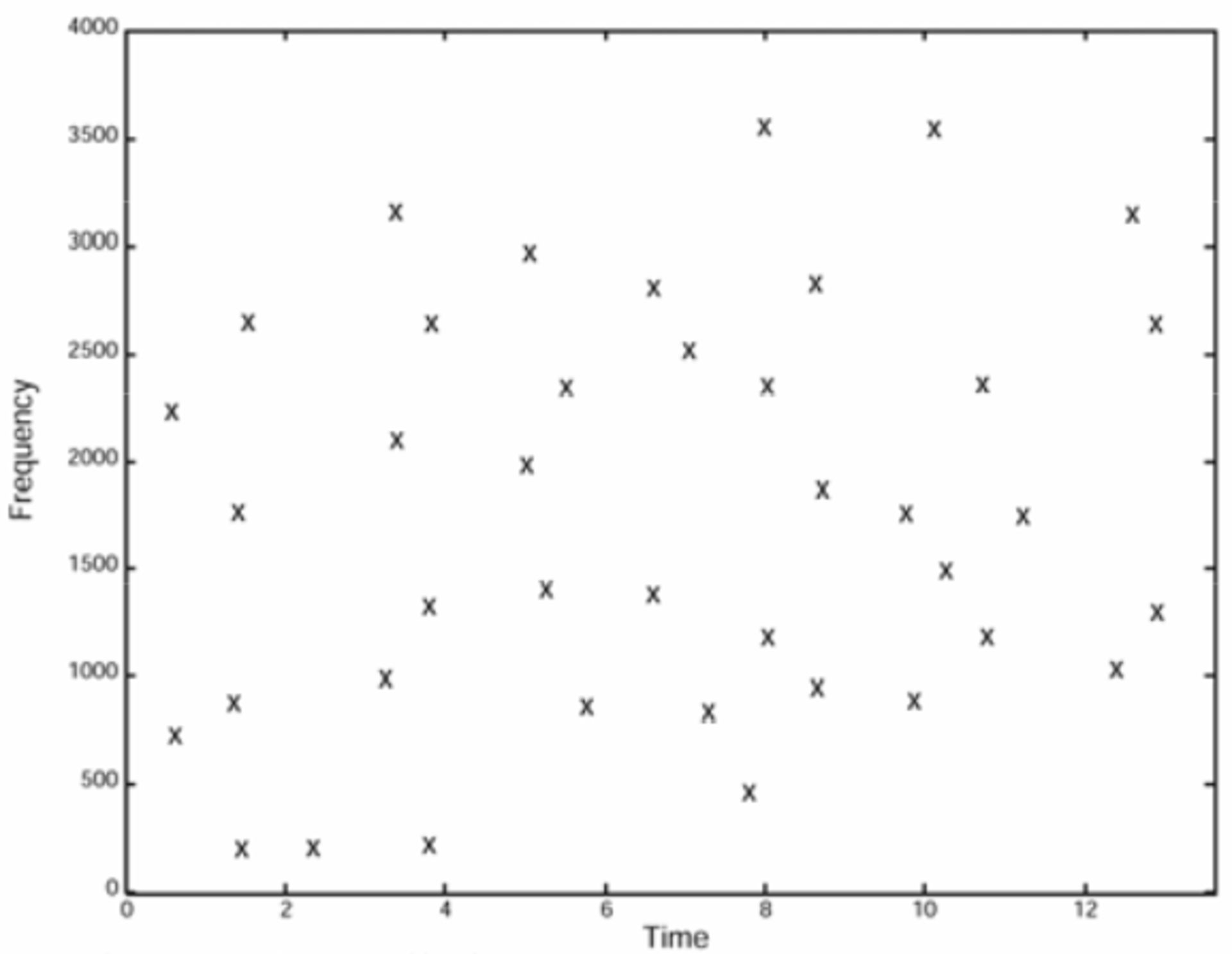
نمودار بالا نیز از مقاله‌ی پژوهشی شزم است و طیف‌نگاره‌‌ی فیلتر‌شده‌ای را نشان می‌دهد. تنها قدرتمندترین فرکانس‌ها از نمودار پیشین حفظ شده‌اند. برخی از بخش‌های موسیقی، مانند ثانیه‌های بین  ۴ تا ۴.۵ فرکانسی ندارند.

تعداد فرکانس‌های موجود در طیف‌نگاره‌ی فیلترشده به ضریب استفاده‌شده در میانگین گام چهارم بستگی دارد، این موضوع به تعداد باندهای مورد استفاده‌ی شما نیز وابسته است. در این نمودارها از ۶ باند استفاده شده است؛ اما این عدد می‌توانست متفاوت باشد.

در این مرحله، شدت فرکانس‌ها سودی به همراه ندارد؛ بنابراین این طیف‌نگاره را می‌توان به‌صورت یک جدول دو ستونی مدل کرد که در آن:

• ستون اول فرکانس‌ها موجود در داخل طیف‌‌نگاره را نشان می‌دهد (محور Y)
• ستون دوم زمانی را نشان می‌دهد که در آن فرکانس ایجاد شده است (محور X)

طیف‌نگاره‌ی فیلتر‌شده هویت صوتی نیست؛ اما بخش عمده‌ای از آن به‌حساب می‌آید. برای کسب اطلاعات بیشتر، بخش بعدی را مطالعه کنید.

یادداشت: در بخش قبلی، الگوریتم ساده‌ای را ارائه دادیم که با آن می‌توان طیف‌نگاره را فیلتر کرد؛ اما استفاده از یک تابع پنجره‌ی لگاریتمی لغزان (اسلایدینگ) و حفظ قدرتمندترین فرکانس‌های بالاتر از مقدار میانگین به اضافه‌ی انحراف استاندارد (ضرب در یک ضریب) از بخش متحرک قطعه‌ی موسیقی می‌تواند راهکار بهتری باشد؛ اما این راهکار بسیار دشوار است؛ از این رو از تشریح آن صرف‌نظر می‌کنیم.

در این مرحله، طیف‌نگاره‌ی فیلترشده‌ای از موسیقی را در اختیار داریم؛ اما چگونه می‌توان آن را ذخیره کرد و به‌صورت بهینه‌ای به‌کار گرفت؟ این بخش، نقطه‌ی قوت شزم محسوب می‌شود. برای درک مسئله، راهکار ساده‌ای را شرح می‌دهیم که در آن با استفاده‌ی مستقیم از طیف‌نگاره‌های فیلترشده به جست‌وجوی یک قطعه‌ی موسیقی می‌پردازیم.

پیش‌نیاز: در ابتدا دیتابیسی از طیف‌نگاره‌های فیلترشده را برای مجموعه‌ای از قطعات موسیقی محاسبه می‌کنیم

گام اول: ۱۰ ثانیه از یک قطعه‌ی موسیقی را ضبط می‌کنیم

گام دوم: طیف‌نگاره‌ی فیلترشده‌ی این ۱۰ ثانیه‌ را محاسبه می‌کنیم

گام سوم: این طیف‌نگاره‌ی کوچک را با طیف‌نگاره‌ی کامل تمام قطعات موسیقی مقایسه می‌کنیم. چگونه می‌توان طیف‌نگاره‌ی ۱۰ ثانیه‌ای را با طیف‌نگاره‌ی ۱۸۰ قطعه‌ی موسیقی مقایسه کرد؟ در ادامه این مساله را به‌صورت شهودی شرح می‌دهیم:

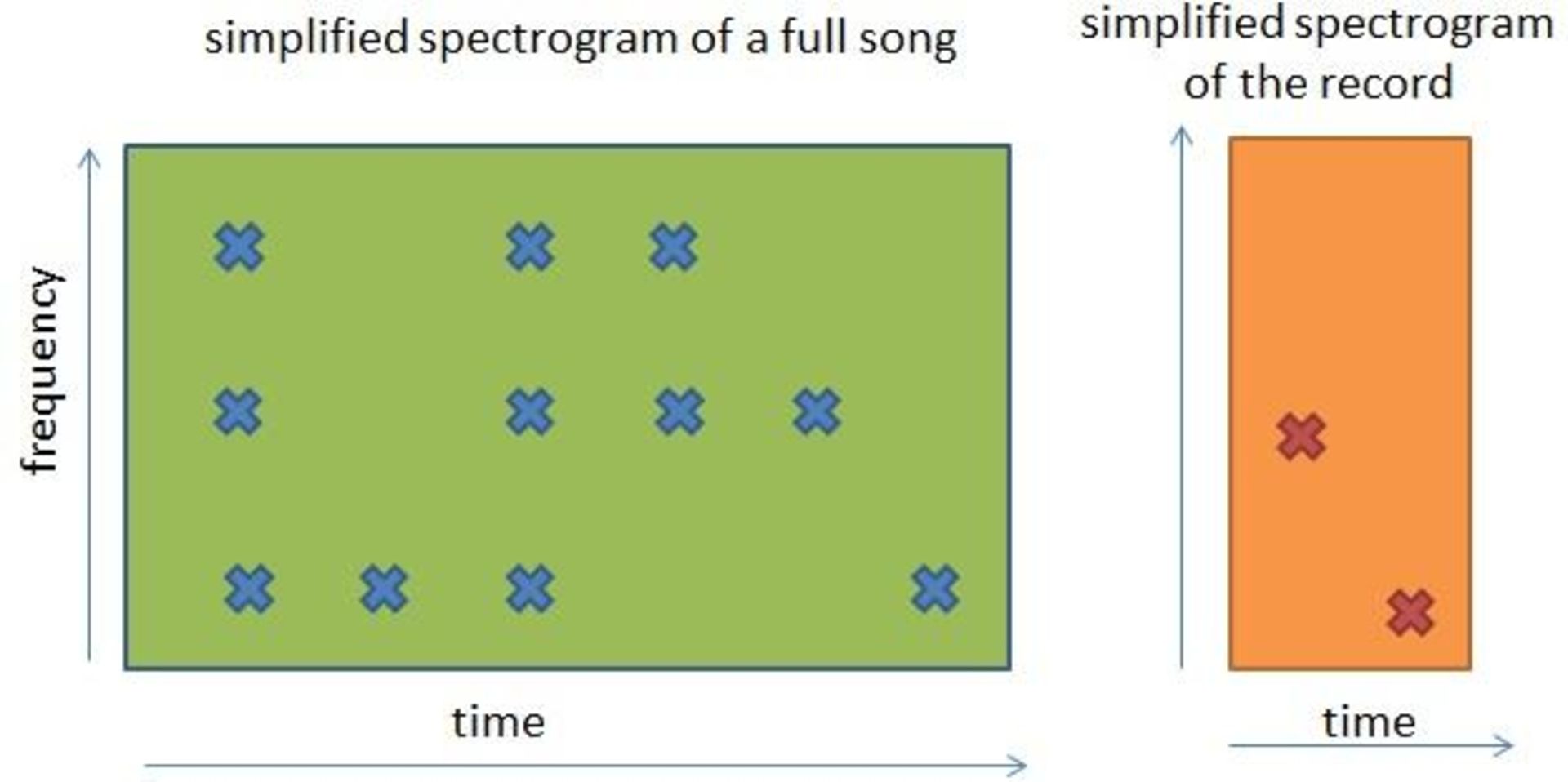
به‌ بیان ساده، باید طیف‌نگاره‌ی کوچک را با تمام بخش‌های طیف‌نگاره‌ی کامل یک قطعه‌ی موسیقی منطبق کرد تا متوجه شد که آیا طیف‌نگاره‌ی کوچک‌تر با بخشی از یک طیف‌نگاره‌ی کامل مطابقت دارد یا خیر.

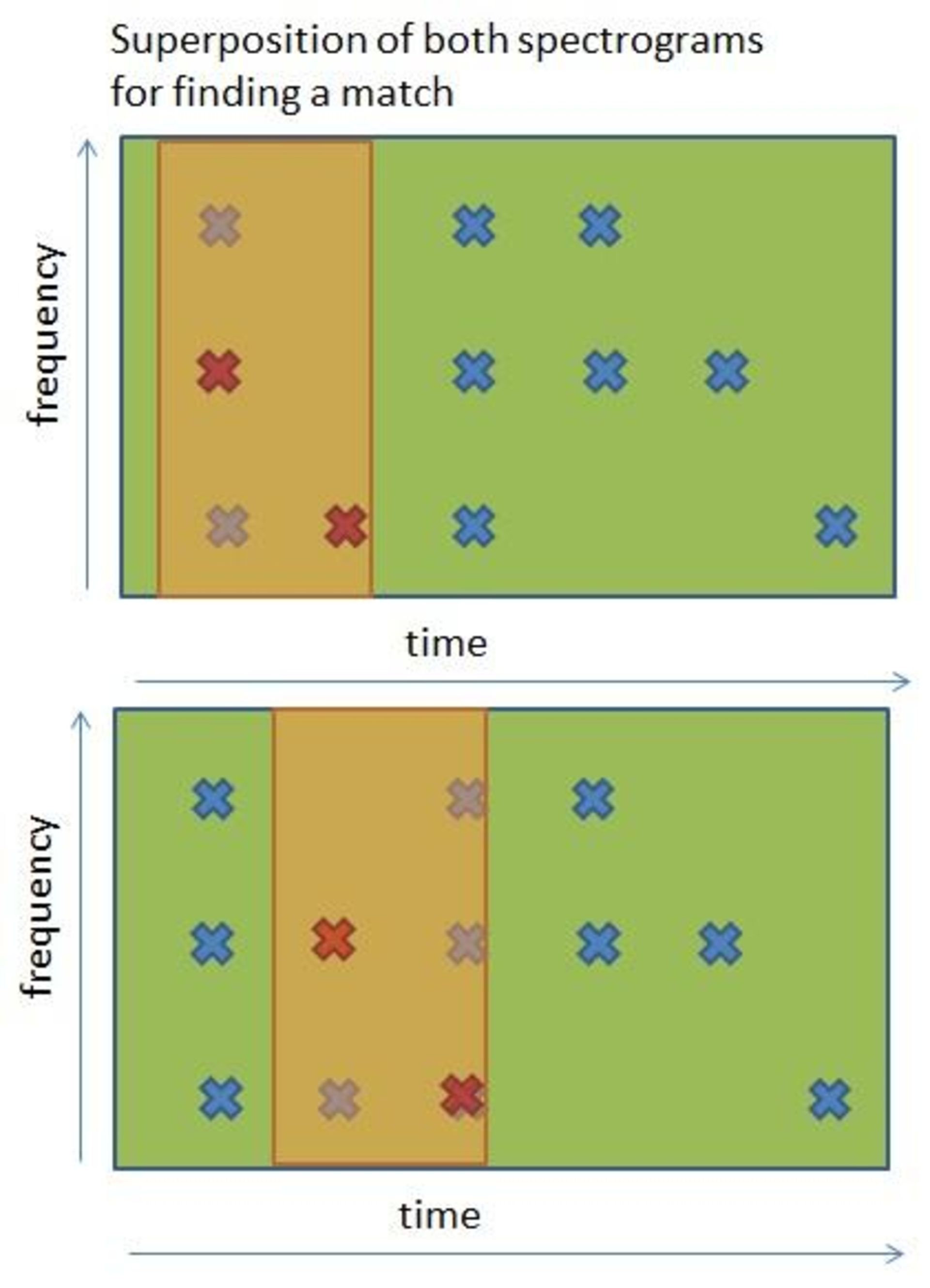
این فرآیند باید برای تمام قطعات موسیقی موجود صورت بگیرد تا در نهایت بتوان موسیقی صحیح را پیدا کرد.

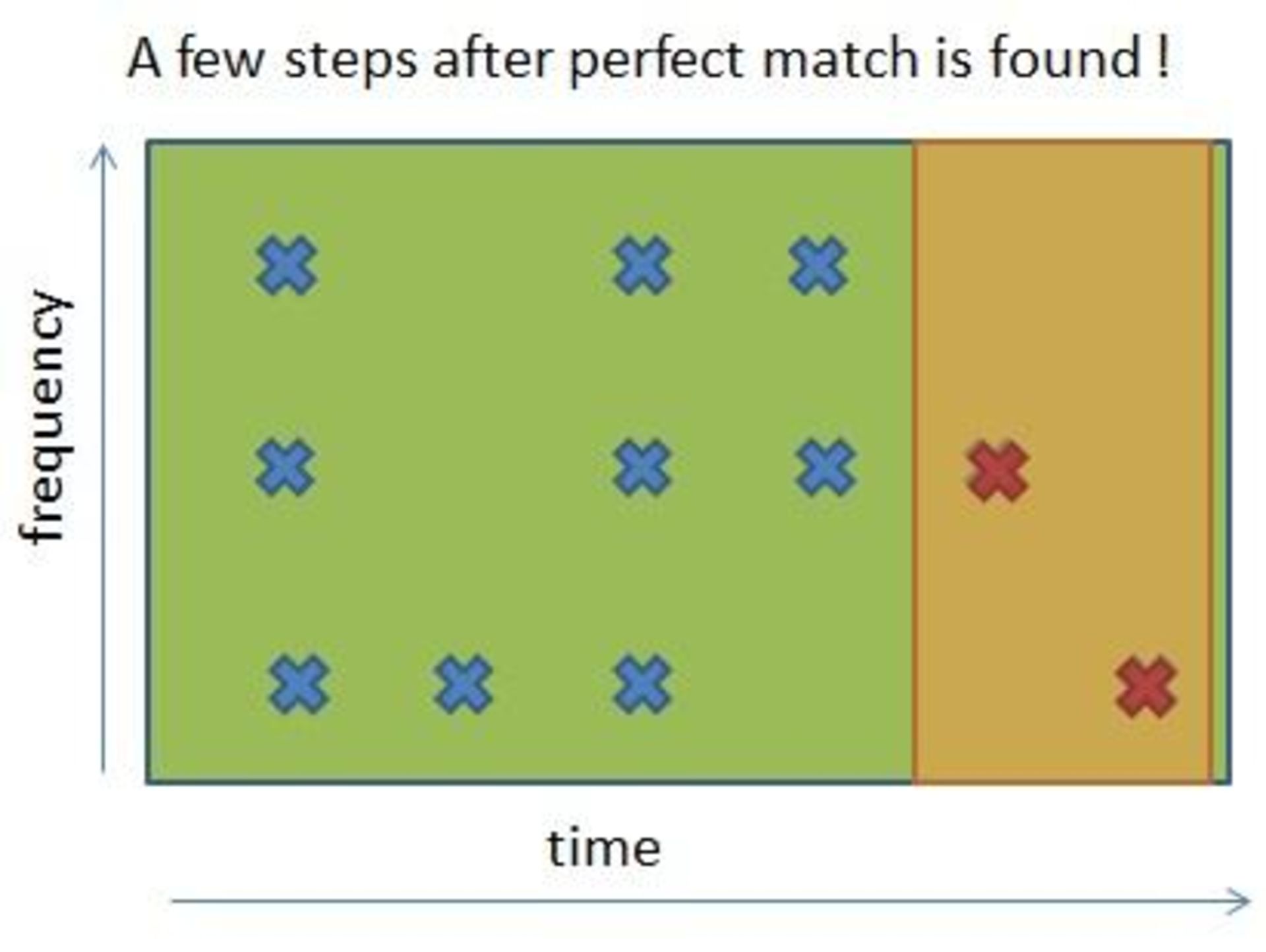
در این مثال، بین فایل ضبط‌شده و قسمت انتهایی قطعه‌ی موسیقی مطابقت وجود دارد؛ اگر چنین نبود، باید فایل ضبط‌شده را با قطعه‌ی دیگری مطابقت داد، این فرآیند تا زمانی ادامه می‌یابد که قطعه‌ی موسیقی صحیح پیدا شود. اگر بهترین گزینه پیدا نشد، می‌توان نزدیک‌ترین گزینه با نرخ تطابق بالاتر از حد آستانه را انتخاب کرد؛ به‌عنوان مثال، اگر نزدیک‌ترین گزینه، نرخ تطابق ۹۰ درصدی داشته‌باشد، می‌توان فرض کرد که این قطعه‌ی موسیقی، گزینه‌ی مورد نظر است؛ چرا که بی‌شک تفاوت ۱۰ درصدی، ناشی از وجود نویزهای خارجی است.

اگرچه این راهکار، عملکرد مناسبی دارد؛ اما نیازمند زمان پردازش بسیار زیادی است. راهکار یادشده باید تمام احتمالات مربوط به تطابق فایل ۱۰ ثانیه‌ای با هر قطعه‌ی موسیقی را محاسبه کند. فرض کنیم که‌ به‌طور متوسط، هر قطعه‌ی موسیقی، در هر ۰.۱ ثانیه، ۳ فرکانس بیشینه داشته باشد؛ بنابراین، فایل ۱۰ ثانیه‌ای ضبط‌شده، ۳۰۰ نقطه‌ی زمان – فرکانس دارد. در بدترین حالت، باید ۳۰۰ در ۳۰۰ در ۳۰ در S محاسبه انجام داد که در آن، S تعداد قطعات موسیقی موجود در کلکسیون شما است. اگر شما ۳۰ هزار فایل موسیقی داشته باشید (۱۰۶ × ۷ ثانیه) زمان پردازش بسیار طولانی خواهد بود و شزم با داشتن کلکسیون ۴۰ میلیون قطعه‌ی موسیقی، زمانی فوق‌العاده طولانی را برای انجام پردازش خواهد طلبید.

بنابراین شزم فرآیند شناسایی موسیقی را چگونه به‌صورت بهینه انجام می‌دهد؟

به‌جای مقایسه‌ی تک‌تک نقاط، می‌توان در آنِ واحد، به‌دنبال چندین نقطه بود. در مقاله‌ی شزم، به این گروه از نقاط، منطقه‌ی هدف گفته می‌شود. در مقاله‌ی یادشده چگونگی تولید این مناطق هدف شرح داده نشده؛ اما احتمالا بدین شکل است: (با هدف درک بهتر، ابعاد مناطق هدف روی ۵ نقطه‌ی زمان – فرکانس تنظیم شده است)

برای حصول اطمینان از اینکه فایل ضبط‌شده و قطعه‌ی کامل موسیقی، مناطق هدف یکسانی را تولید می‌کنند، به یک رابطه‌ی ترتیبی بین نقاط زمان – فرکانس در طیف‌نگاره‌ی فیلترشده نیاز داریم:

• اگر دو نقطه‌ی زمان – فرکانس، زمان یکسانی داشته باشند، نقطه‌ی زمان – فرکانس با پایین‌ترین فرکانس، پیش از نمونه‌ی دیگر قرار دارد
• اگر یک نقطه‌ی زمان – فرکانس، زمان پایین‌تری نسبت به دیگری داشته باشد؛ پس از آن پیش است

اگر این قاعده را روی طیف‌نگاره‌ی ساده‌شده‌ی پیشین پیاده کنیم، به این نتیجه خواهیم رسید:

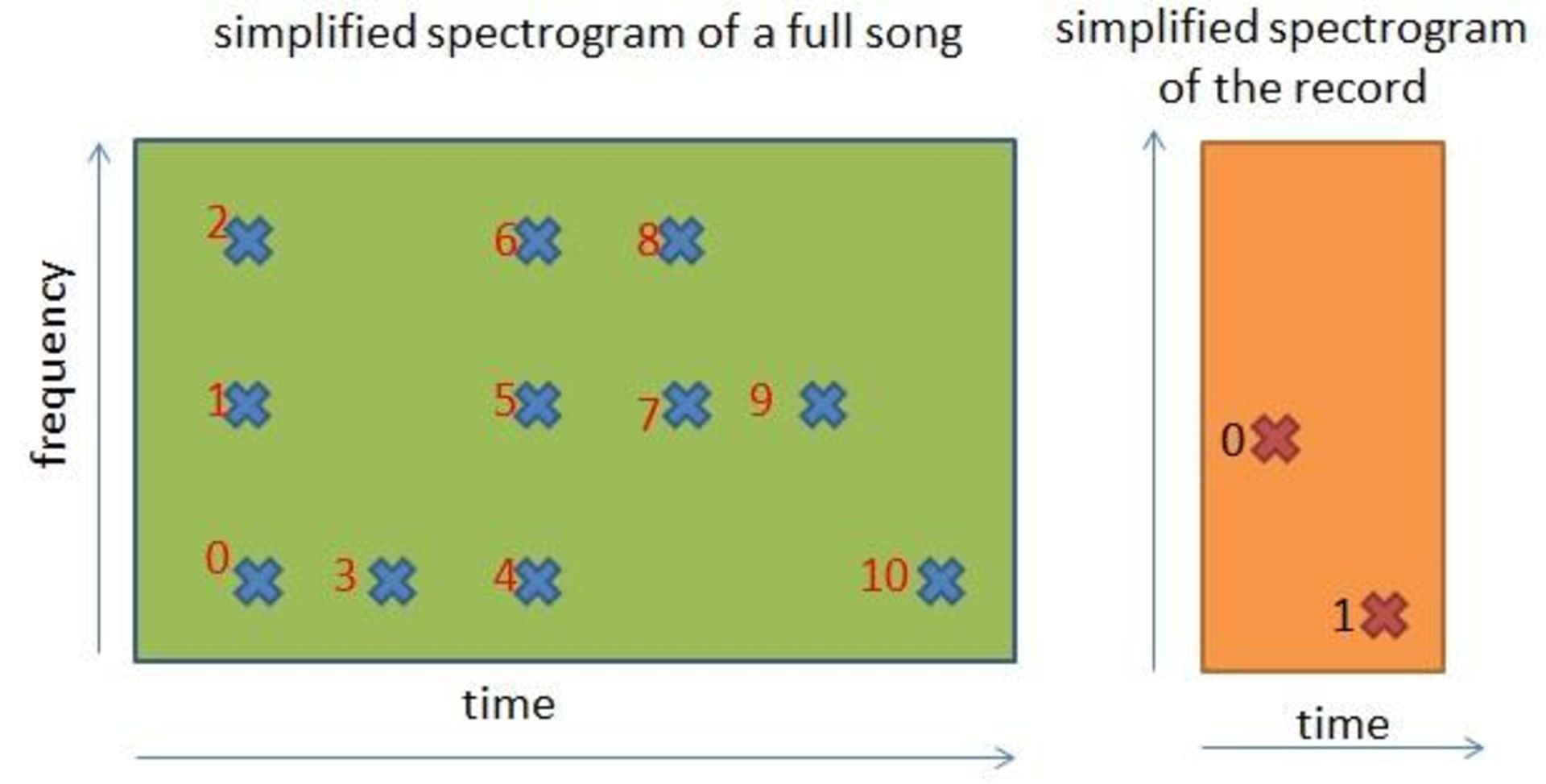
در این نمودار، تمام نقاط زمان – فرکانس با استفاده از این رابطه‌ی ترتیبی، علامت‌گذاری شده‌اند؛ به‌عنوان مثال:

• نقطه‌ی صفر پیش از نقاط دیگر در طیف‌نگاره قرار دارد
• نقطه‌ی ۲ پس از نقطه‌ی ۰ و ۱؛ اما پیش از سایر نقاط قرار دارد

حال که می‌توان به داخل طیف‌نگاره ترتیب بخشید، می‌توانیم با استفاده از این قانون، مناطق هدف یکسانی را در طیف‌نگاره‌های مختلف ایجاد کنیم: «برای تولید مناطق هدف داخل یک طیف‌نگاره باید برای هر نقطه‌ی زمان – فرکانس، گروهی شامل این نقطه و چهار نقطه پس از آن ایجاد کنیم.» بدین ترتیب، تعداد مناطق هدف تقریبا با تعداد نقاط برابری خواهد کرد. این تولید گروه برای قطعه‌ی موسیقی یا فایل ضبط‌شده یکسان است.

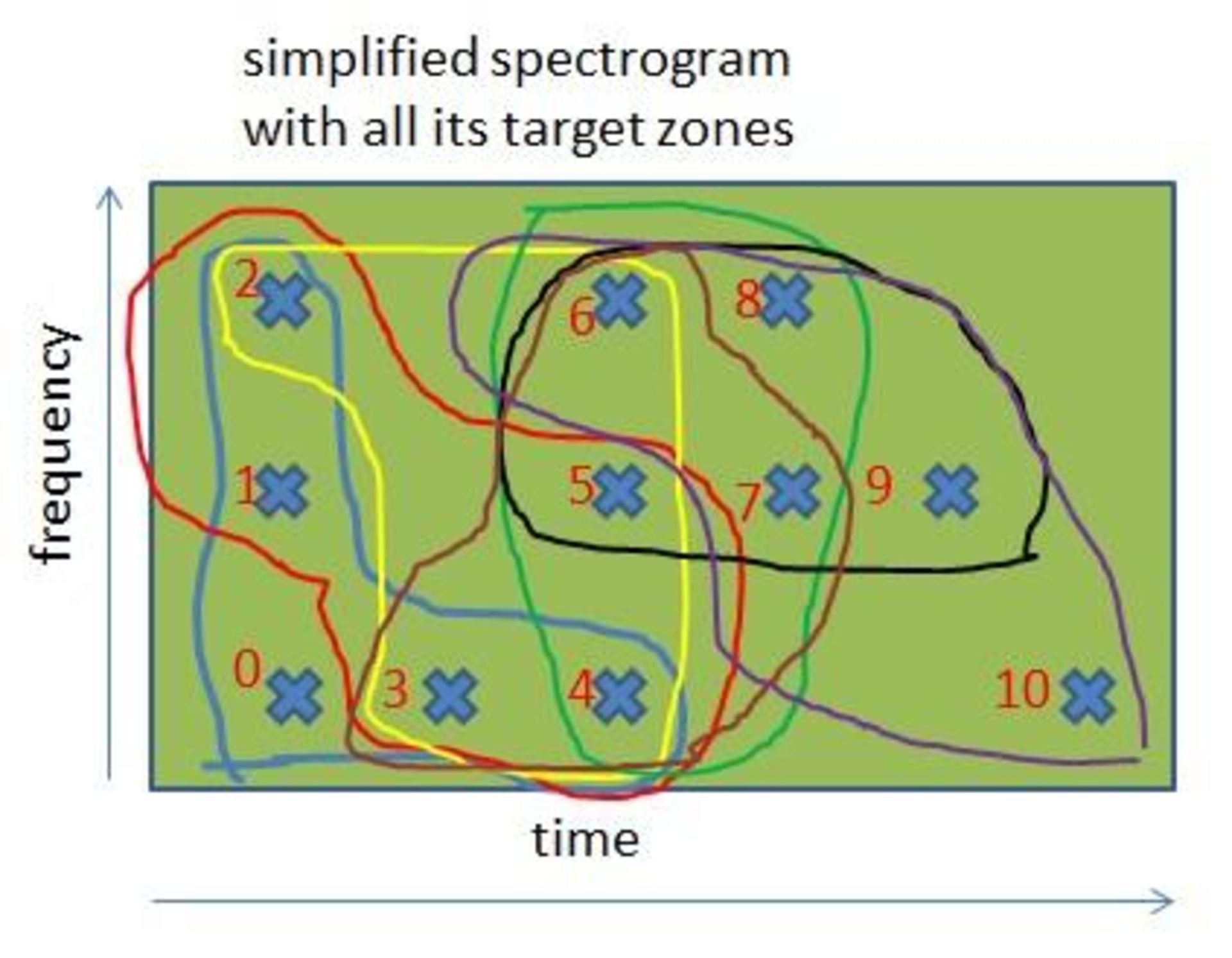
در این طیف‌نگاره‌ی ساده‌شده، می‌توان مناطق هدف متفاوت ایجاد‌شده توسط الگوریتم پیشین را مشاهده کرد. از آنجایی که ابعاد هدف ۵ است، به غیر از نقاط ابتدایی و انتهایی طیف‌نگاره، اغلب نقاط درون مناطقی با ۵ هدف جای دارند.

یادداشت: شاید چرایی لزوم محاسبه‌ی تعداد زیادی از مناطق هدف را متوجه نباشید. ما می‌توانستیم مناطق هدف را با چنین قانونی تولید کنیم: «برای هر نقطه با برچسبی از حاصل‌ضرب ۵، باید گروهی شامل این فرکانس و ۴ فرکانس پس از آن ایجاد کنید». با این قانون ۵ عدد از تعداد مناطق هدف و زمان مرود نیاز برای جست‌وجو کاهش پیدا می‌کرد؛ اما باید خاطرنشان کنیم که محاسبه‌ی تمام مناطق هدف محتمل در فایل ضبط‌شده و قطعه‌ی موسیقی، مقاومت در برابر نویز را به‌مقدار زیادی افزایش می‌دهد.

اکنون چندین منطقه‌ی هدف داریم؛ اما گام بعدی چیست؟ باید برای هر نقطه، آدرسی را برمبنای آن منطقه‌های هدف ایجاد کنیم. برای ایجاد چنین آدرس‌هایی، باید به ازای هر منطقه‌ی هدف، یک نقطه‌ی لنگر (Anchor Point) نیز نیاز داریم؛ اما در مقاله‌ی شزم، چگونگی انجام این کار نیز شرح داده نشده است. فرض می‌کنیم که نقطه‌ی لنگر، سومین نقطه پیش از منطقه‌ی هدف باشد. نقطه‌ی لنگر می‌تواند در هر نقطه‌ای باشد؛ به‌شرط آنکه با همان روش ابتدایی، قابل تولید مجدد باشد و این موضوع به‌لطف رابطه‌ی ترتیبی به‌دست آمده است.

در این تصویر، دو منطقه‌ی هدف به‌همراه نقطه‌ی لنگر آن‌ها ترسیم شده‌اند. به منطقه‌ی هدف بنفش توجه کنید. رابطه‌ی آدرس پیشنهاد‌شده توسط شزم بدین شکل است:

{«اختلاف زمانی بین لنگر و نقطه»؛ «فرکانس نقطه»؛ «فرکانس لنگر»}

برای منطقه‌ی بنفش داریم:

• آدرس نقطه‌ی ۶ عبارت است از : {«دلتای زمانی بین نقطه‌ی ۳ و نقطه‌ی ۶»؛ «فرکانس نقطه‌ی ۶»؛ «فرکانس ۳»}؛ بنابراین داریم: {۱؛۳۰؛۱۰}
• آدرس نقطه‌ی ۷ عبارت است از: {۲؛۲۰؛۱۰}

هر دو نقطه در منطقه‌ی قهوه‌ای نیز ظاهر شده‌اند، آدرس آن‌ها در این منطقه‌ی هدف عبارت از : {۲؛۳۰؛۱۰} برای نقطه‌ی ۶ و {۳؛۲۰؛۱۰} برای نقطه‌ی ۷ است.

خاطرنشان می‌کنیم که آدرس‌ها با عاملی مرتبط هستند. در مورد قطعات کامل موسیقی (بنابراین تنها در سمت سرور)، این آدرس‌ها با {«ID موسیقی»؛ «زمان مطلق لنگر در موسیقی»} مرتبط هستند. در نمونه‌ی ما برای دو نقطه‌ی پیشین، نتایج بدین شکل هستند:

[10;30;1]–>[2;1][10;30;2]–>[2;1][10;30;2]–>[1;1][10;30;3]–>[1;1]

اگر این منطق را روی تمام نقاط موجود در تمام مناطق هدف طیف‌نگاره‌ی کل قطعات موسیقی پیاده کنید، جدول دو ستونی بسیار بزرگی را به‌دست خواهید آورد

• آدرس‌ها
• جفت («آی‌دی موسیقی»؛ «زمان لنگر»)

این جدول، دیتابیس هویت صوتی شزم محسوب می‌شود. اگر به‌صورت متوسط هر قطعه‌ی موسیقی در هر ثانیه ۳۰ فرکانس اوج داشته باشد و ابعاد منطقه‌ی هدف را نیز ۵ در نظر بگیریم، ابعاد جدول ۵ در ۳۰ در S خواهد بود که در آن S تعداد ثانیه‌های کل کلکسیون موسیقی است.

اگر به‌خاطر داشته باشید، ما از تبدیل سریع فوریه‌ی ۱۰۲۴ نمونه‌ای استفاده کردیم؛ بدین مفهوم که تنها ۵۱۲ مقدار محتمل فرکانس وجود دارد. این فرکانس‌ها می‌توانند در ۹ بیت (۵۱۲ = ۲۹) کُد شوند. اگر فرض کنیم دلتای زمان (اختلاف زمانی) در حد میلی‌ثانیه باشد، هیچ‌گاه بیشتر از ۱۶ ثانیه نخواهد بود؛ چرا که مفهوم آن، یک قطعه‌ با ۱۶ ثانیه‌ی بدون موسیقی (یا صدایی بسیار پایین) است؛ بنابراین می‌توان دلتای زمان را در ۱۴ بیت (۱۶۳۸۴ = ۲۱۴) کُد کرد. آدرس می‌تواند در قالب عد صحیح (Integer) ۳۲ بیتی کُد شود.

• ۹ بیت برای «فرکانس لنگر»
• ۹ بیت برای «فرکانس نقطه»
• ۱۴ بیت برای «دلتای زمان بین لنگر و نقطه»

با استفاده از همان منطق می‌توان، جفت («آی‌دی موسیقی»؛ «زمان لنگر») در قالب عدد صحیح ۶۴ بیتی کد کرد (۳۲ بیت برای هرکدام).

جدول هویت صوتی را می‌توان در قالب آرایه‌ی ساده‌ای از اعداد صحیح ۶۴ بیتی پیاده‌سازی کرد:

• اندیس (نمایه‌) آرایه آدرسی در قالب عدد صحیح ۳۲ بیتی است
• لیست اعداد صحیح ۶۴ بیتی، تمام جفت‌های این آدرس است

به‌عبارت دیگر، جدول هویت صوتی را به یک پروسه‌ی جست‌وجوی وارونه بدل کردیم که امکان اجرای فرآیند جست‌وجو با زمانی بسیار مؤثر یا (O(1 را می‌دهد.

یادداشت: احتمالا متوجه شده‌اید که نقطه‌ی لنگر موجود در داخل منطقه‌ی هدف را انتخاب نکرده‌ایم؛ به‌عنوان مثال می‌توانستیم اولین نقطه از منطقه‌ی هدف را انتخاب کنیم؛ اگر چنین می‌کردیم، در این حالت آدرس‌های بسیاری به‌ فُرم {۰؛ فرکانس لنگر؛ فرکانس لنگر} ایجاد می‌شد؛ بنابراین جفت‌های («آی‌دی موسیقی»؛ «زمان لنگر») با آدرسی مانند {۰؛ Y؛ Y} به‌وجود می‌آمدند که در‌ آن‌ها Y فرکانسی بین صفر تا ۵۱۱ است.

اکنون در سمت سرور، ساختار داده‌ی بسیار خوبی داریم، اما چگونه می‌توان از آن استفاده کرد؟

برای انجام جست‌وجو، گام مربوط به ایجاد هویت صوتی روی فایل ضبط‌شده اجرا می‌شود تا آدرس / ساختار مقداری تولید شود که به‌لحاظ مقداری، کمی متفاوت است:

{«دلتای زمانی بین لنگر و نقطه»؛ «فرکانس نقطه»؛ «فرکانس لنگر»} -> {«زمان مطلق لنگر در فایل ضبط‌شده»}

در مرحله‌ی بعد، این داده به سمت سرور (شزم) ارسال می‌شود. در این مورد هم، همان فرض قبلی را در نظر می‌گیریم (۳۰۰ نقطه‌ی زمان – فرکانس در طیف‌نگاره‌ی فیلترشده‌ی فایل ۱۰ ثانیه‌ای ضبط‌شده و منطقه‌ی هدف با ابعاد ۵)؛ بدین مفهوم که تقریبا ۱۵۰۰ داده به شزم ارسال شده است.

هر آدرس از فایل ضبط‌شده برای جست‌وجو در دیتابیس هویت صوتی جفت مربوطه {«آی‌دی موسیقی»؛ «زمان مطلق لنگر در قطعه‌ی موسیقی»} استفاده می‌شود. به‌لحاظ پیچیدگی زمانی، با فرض اینکه دیتابیس هویت صوتی in-memory‌ (نوعی از پایگاه داده که عمدتا برای ذخیره‌سازی داده به حافظه‌ی اصلی اتکا دارد) است، در این صورت، هزینه‌ی جست‌وجو با تعداد آدرس‌های ارسال‌شده به شزم متناسب خواهد بود. این جست‌وجو، تعداد بالایی از جفت‌ها (فرض می‌کنیم تعداد جفت‌ها M باشد) را بازمی‌گرداند.

اگرچه M تعداد بسیار بالایی محسوب می‌شود؛ اما از تعداد نت‌های تمام قطعات موسیقی (نقاط زمان - فرکانس) کمتر است. قدرت اصلی پروسه‌ی جست‌وجو یادشده این است که به‌جای جست‌وجوی یک نت داخل موسیقی، وجود دو نت مجزا از دلتای زمانی چند ثانیه‌ای در داخل قطعه‌ی موسیقی را بررسی می‌کند. در پایان این بخش، توضیحات بیشتری درباره‌ی پیچیدگی زمانی ارائه خواهد شد.

اگرچه در مقاله‌ی پژوهشی شزم اشاره‌ای به گام بعدی نشده است؛ اما حدس می‌زنیم که در مرحله‌ی بعد باید، M نتیجه‌‌ی حاصل از جست‌وجو را از طریق حفظ آن دسته از جفت‌های موجود در موسیقی که تعداد کمینه‌ای مناطق هدف مشترک با فایل ضبط‌شده دارند، فیلتر کرد.

به‌عنوان مثال، فرض کنید نتیجه‌ی جست‌وجو بدین شکل باشد:

• ۱۰۰ جفت از قطعه‌ی موسیقی ۱ که صفر منطقه‌ی هدف مشترک با فایل ضبط‌شده دارند
• ۱۰ جفت از قطعه‌ی موسیقی ۲ که صفر منطقه‌ی هدف مشترک با فایل ضبط‌شده دارند
• ۵۰ جفت از قطعه‌ی موسیقی ۵ که صفر منطقه‌ی هدف مشترک با فایل ضبط‌شده دارند
• ۷۰ جفت از قطعه‌ی موسیقی ۸ که صفر منطقه‌ی هدف مشترک با فایل ضبط‌شده دارند
• ۸۳ جفت از قطعه‌ی موسیقی ۱۰۸ که ۳۰ منطقه‌ی هدف مشترک با فایل ضبط‌شده دارند
• ۲۱۰ جفت از قطعه‌ی موسیقی ۱۷ که ۱۰۰ منطقه‌ی هدف مشترک با فایل ضبط‌شده دارند
• ۴۴۰۰ جفت از قطعه‌ی موسیقی ۱۳ که ۲۸۰ منطقه‌ی هدف مشترک با فایل ضبط‌شده دارند
• ۳۵۰۰ جفت از قطعه‌ی موسیقی ۲۵ که ۴۰۰ منطقه‌ی هدف مشترک با فایل ضبط‌شده دارند

فایل ۱۰ ثانیه‌ای ضبط‌شده‌ی ما تقریبا ۳۰۰ منطقه‌ی هدف داشت؛ بنابراین در بهترین حالت داریم:

• قطعه‌ی شماره‌ی ۱ و فایل ضبط‌شده نسبت تطابق صفر درصدی دارند
• قطعه‌ی شماره‌ی ۲ و فایل ضبط‌شده نسبت تطابق صفر درصدی دارند
• قطعه‌ی شماره‌ی ۵ و فایل ضبط‌شده نسبت تطابق صفر درصدی دارند
• قطعه‌ی شماره‌ی ۸ و فایل ضبط‌شده نسبت تطابق صفر درصدی دارند
• قطعه‌ی شماره‌ی ۱۰ و فایل ضبط‌شده نسبت تطابق ۱۰ درصدی دارند
• قطعه‌ی شماره‌ی ۱۷ و فایل ضبط‌شده نسبت تطابق ۳۳ درصدی دارند
• قطعه‌ی شماره‌ی ۱۳ و فایل ضبط‌شده نسبت تطابق ۹۱.۷ درصدی دارند
• قطعه‌ی شماره‌ی ۲۵ و فایل ضبط‌شده نسبت تطابق ۱۰۰ درصدی دارند

تنها قطعات شماره‌ی ۱۳ و ۲۵ را از نتایج حفظ خواهیم کرد. اگرچه قطعات شماره‌ی ۱، ۲، ۵ و ۸ چندین زوج مشترک با فایل ضبط‌شده دارند، هیچ‌کدام حداقل یک منطقه‌ی هدف ۵ نقطه‌ای مشترک با فایل ضبط‌شده شکل نمی‌دهند. این گام می‌تواند چندین نتیجه‌ی کاذب را فیلتر کند؛ زیرا دیتابیس هویت صوتی شزم، تعداد بسیار بالایی از جفت‌ها با آدرس یکسان دارد و شما به‌سادگی می‌توانید به جفت‌هایی با آدرس یکسان برسید که به منطقه‌ی هدف یکسانی تعلق ندارند. اگر دلیل این موضوع را متوجه نمی‌شوید، به تصویر پایانی از بخش پیشین توجه کنید: آدرس {۲؛ ۳۰؛ ۱۰} توسط دو نقطه‌ی زمان – فرکانس استفاده می‌شود که به منطقه‌ی هدف یکسانی تعلق ندارند. اگر فایل ضبط‌شده نیز چنین آدرسی داشته باشد، حداقل یکی از دو جفت در نتایج فیلتر خواهد شد.

این گام می‌تواند در O(M) توسط یک جدول هش صورت بگیرد که کلید آن {زمان مطلق لنگر در موسیقی؛ آی‌دی موسیقی} و تعداد دفعاتی است که در نتیجه پدیدار می‌شود:

• پروسه را در M نتیجه تکرار کرده و تعداد دفعاتی که یک جفت در جدول هش حضور دارد، به‌دست می‌آوریم
• تمام جفت‌هایی (کلید جدول هش) که کمتر از ۴ بار پدیدار شده‌اند، حذف می‌کنیم؛ به‌عبارت دیگر، تمام نقاطی را که منطقه‌ی هدف شکل نمی‌دهند، حذف می‌کنیم*
• تعداد دفعاتی را که آی‌دی موسیقی بخشی از کلید در جدول هش است، محاسبه می‌کنیم (تعداد مناطق هدف کامل در موسیقی را به‌دست می‌آوریم. از آنجایی که جفت از جست‌وجو حاصل می‌شود، مناطق هدف یادشده نیز در فایل ضبط‌شده وجود دارند)
• تنها نتایجی را نگه می‌داریم که در آن‌ها شماره‌ی موسیقی، بالاتر از ۳۰۰ در ضریب است (۳۰۰ تعداد مناطق هدف در فایل ضبط‌شده است و ما این عدد را به‌دلیل وجود نویز، با یک ضریب کاهش می‌دهیم)
• نتایج باقی‌مانده را در جدول هش جدیدی قرار می‌‌دهیم که اندیس آن آی‌دی موسیقی است (این هش‌مپ در گام بعدی سودمند خواهد بود)

* هدف از این کار،‌ جست‌وجو برای منطقه‌ی هدفی است که توسط یک نقطه‌ی لنگر در موسیقی ایجاد شده است. این نقطه‌ی لنگر را می‌توان با آی‌دی قطعه‌ای که به آن تعلق دارد و زمان مطلقی که در آن رخ می‌دهد، تعریف کرد. ما تقریبی را صورت دادیم؛ زیرا داخل یک موسیقی، می‌‌توان چندین نقطه‌ی لنگر در آنِ واحد داشت. از آنجایی که با یک طیف‌نگاره‌ی فیلتر‌شده سروکار داریم، در آنِ واحد، نقاط لنگر زیادی نخواهیم داشت؛ اما کلید {زمان مطلق لنگر در یک موسیقی؛ آی‌دی موسیقی} تمام مناطق هدف ایجادشده با این نقاط هدف را گردآوری خواهد کرد.

یادداشت: ما در این الگوریتم ۲ جدول هش استفاده کردیم. اگر با سازوکار آن آشنا نیستید، این روش را به‌عنوان راهکار بسیار بهینه‌ای برای ذخیره‌سازی و به‌دست‌آوردن داده در نظر بگیرید. اگر تمایل دارید تا در این باره اطلاعات بیشتری کسب کنید، به این لینک مراجعه کنید.

در این مرحله، تنها قطعاتی را در اختیار داریم که بسیار نزدیک به فایل ضبط‌شده هستند؛ اما کماکان باید هم‌سازی زمانی بین نت‌های فایل ضبط‌شده و این قطعات را بررسی کنیم. در ادامه دلیل این موضوع را متوجه خواهید شد:

در این تصویر، دو منطقه‌ی هدف را مشاهده می‌کنیم که به دو قطعه‌ی موسیقی متفاوت تعلق دارند. اگر به‌دنبال هم‌سازی زمانی نبودیم، مناطق هدف یادشده، امتیاز تطابق بین این دو قطعه‌ی موسیقی را افزایش می‌دادند؛ در حالی که صدای مشابهی تولید نمی‌کنند؛ زیرا نت‌های موجود در آن مناطق هدف با ترتیب یکسانی نواخته نمی‌شوند.

گام پایانی درباره‌ی ترتیب زمانی است:

• محاسبه‌ی نت‌های قطعات موسیقی باقی‌مانده و زمان مطلق این نت‌ها در داخل قطعه
• تکرار فرآیند یادشده برای فایل ضبط‌شده که نت‌ها و زمان مطلق آن‌ها در فایل را به‌دست می‌دهد
• چنانچه نت‌های موجود در داخل قطعه‌ی موسیقی و فایل ضبط‌شده هم‌ساز زمانی باشند، باید چنین ترتیبی را پیدا کنیم: «زمان مطلق نت در داخل قطعه‌ی موسیقی = زمان مطلق نت در فایل ضبط‌شده + دلتای زمانی» که در آن دلتای زمانی معادل زمان آغاز قسمتی از موسیقی است که با فایل ضبط‌شده مطابقت دارد
• برای هر قطعه‌ی موسیقی باید دلتایی را بیابیم که بیش‌ترین تعداد نت‌های منطبق با این ترتیب زمانی را به‌دست می‌دهد
• سپس قطعه‌ای را انتخاب می‌کنیم که بیش‌ترین تعداد نت‌های هم‌ساز با فایل ضبط‌شده را دارد

اکنون با ساز‌وکار این بخش آشنا شدید، حال به‌سراغ فرآیند فنی انجام آن می‌رویم. در این مرحله لیستی از آدرس‌ها / مقادیر را برای فایل ضبط‌شده در اختیار داریم:

{«زمان مطلق لنگر در فایل ضبط‌شده»} <- {«دلتای زمانی بین لنگر و نقطه»؛ «فرکانس نقطه»؛ «فرکانس لنگر»}

ما برای هر قطعه‌ی موسیقی نیز لیستی از آدرس / مقادیر داریم که در جدول هش گام پیشین ذخیره‌ شده‌اند:

{«آی‌دی موسیقی»؛ «زمان مطلق لنگر در موسیقی»} <- {«دلتای زمانی بین لنگر و نقطه»؛ «فرکانس نقطه»؛ «فرکانس لنگر»}

روی قطعات موسیقی باقی‌مانده باید فرآیند‌های زیر پیاده شوند:

• برای هر آدرس در فایل ضبط‌شده، مقدار مربوطه را از قطعه‌‌ی موسیقی به‌دست‌ آورده و دلتای زمانی را محاسبه می‌‌‌کنیم: «زمان مطلق لنگر در قطعه‌ی موسیقی» - «زمان مطلق لنگر در فایل ضبط‌شده» سپس مقدار به‌دست آمده را در «لیست دلتا» قرار می‌دهیم
• ممکن است آدرس موجود در فایل ضبط‌شده با چندین مقدار در موسیقی مرتبط باشد (چندین نقطه در مناطق هدف مختلف موسیقی)، در این حالت دلتای زمانی برای هرکدام از مقادیر محاسبه می‌کنیم و در لیست دلتا قرار می‌دهیم
• برای هر مقدار متفاوت دلتا در «لیست دلتا»، تعداد دفعات وقوع آن را می‌شماریم (به‌عبارت دیگر، برای هر دلتا، تعداد نت‌هایی را می‌شماریم که از قانون «دلتا + زمان مطلق نت در فایل ضبط‌شده = زمان مطلق نت در موسیقی» تبعیت می‌کند)
• در نهایت بزرگ‌ترین مقدار را نگه می‌داریم (این مقدار بیش‌تر‌ین تعداد نت‌هایی را می‌دهد که بین فایل ضبط‌شده و قطعه‌ی موسیقی هم‌ساز است)

از بین تمام قطعات موسیقی، قطعه‌ای را نگه می‌داریم که بیش‌ترین تعداد نت‌‌های هم‌ساز را داشته باشد. چنانچه این هم‌سازی فراتر از «تعداد نت‌های داخل فایل ضبط‌شده» × «یک ضریب» باشد، پس قطعه‌ی یادشده، همان موسیقی مورد نظر است.

حال باید به‌دنبال متادیتای قطعه‌ی مورد نظر («نام هنرمند»، «نام موسیقی»، «لینک موسیقی در آیتونز»، «لینک موسیقی در آمازون» و ...) باشیم و با آی‌دی موسیقی، نتیجه را به کاربر بازگردانیم.

این جست‌وجو بسیار پیچیده‌تر از نمونه‌ی ساده‌ای است که در ابتدا مشاهده کردیم، آیا این فرآیند ارزش صرف وقت را دارد؟ فرآیند جست‌وجوی بهبود‌یافته، راهکار گام‌به‌گامی است که در هر گام از میزان پیچیدگی می‌کاهد.

برای درک بهتر، مجددا فرضیات ابتدایی را یادآوری می‌کنیم و برای ساده‌سازی مساله، فرضیات بیشتری را در نظر می‌گیریم:

• ۵۱۲ فرکانس محتمل را در اختیار داریم
• به‌طور متوسط، هر قطعه‌ی موسیقی، در هر ثانیه، ۳۰ فرکانس اوج دارد
• بنابراین یک فایل ضبط‌شده‌ی ۱۰ ثانیه‌ای، ۳۰۰ نقطه‌ی زمان – فرکانس دارد
• S تعداد کل ثانیه‌های تمام قطعات موسیقی است
• ابعاد منطقه‌ی هدف ۵ نت است
• فرض جدید: فرض می‌کنیم دلتای زمانی بین یک نقطه‌ و لنگر آن صفر یا ۱۰ میلی‌ثانیه باشد
• فرض جدید: فرض می‌کنیم تولید آدرس‌ها به‌صورت یکنواخت توزیع شده باشد؛ بدین مفهوم که برای هر آدرس {T، Y، X}، تعداد یکسانی از جفت‌ها وجود داشته باشد که در آن X و Y یکی از ۵۱۲ فرکانس هستند؛ در حالی که T صفر یا ۱۰ میلی‌ثانیه است

جست‌وجو، گام نخست به تنها ۵ × ۳۰۰ جست‌وجوی واحد نیاز دارد. ابعاد جست‌وجوی M با مجموع نتایج حاصل از ۵ × ۳۰۰ جست‌وجوی واحد برابر است.

M = (5 * 300)*(S * 30 * 5 * 300)/(512 * 512 * 2)

گام دوم، فیلتر نتایج را می‌توان در M‌ عملیات انجام داد. در پایان این مرحله، N نت توزیع‌شده در Z موسیقی وجود دارد. بدون آنالیز آماری مجموعه‌ی موسیقی، به‌دست آوردن مقادیر N و Z ممکن نیست. به‌نظر می‌رسد که N بسیار پایین‌تر از M و Z است و حتی برای دیتابیسی مانند شزم با ۴۰ میلیون قطعه موسیقی، تنها چند موسیقی را به نمایش می‌گذارد.

گام پایانی به آنالیز هم‌سازی زمانی Z موسیقی مربوط می‌شود. فرض می‌کنیم که هر قطعه‌ی موسیقی به‌صورت تقریبی تعداد نت‌های یکسانی دارد:‌ N/Z. در بدترین شرایط (فایل ضبط‌شده از یک قطعه‌ی موسیقی که تنها یک نت به‌صورت مداوم در آن نواخته می‌شود)، پیچیدگی یک آنالیز (5*300) * (N/Z) خواهد بود؛ بدین ترتیب هزینه‌ی محاسباتی Z قطعه‌ی موسیقی N × ۳۰۰ × ۵ خواهد شد.

از آنجایی که N بسیار کوچک‌تر از M  است (N<

M = (300 * 300 * 30 * S)*(5 * 5)/(512 * 512 * 2)

اگر به‌خاطر داشته باشید، هزینه‌ی انجام فرآیند جست‌وجوی ساده، ۳۰۰ × ۳۰۰ × ۳۰ × S بود. بنابراین فرآیند جست‌وجوی جدید ۲۰ هزار بار سریع‌تر است.

یادداشت: پیچیدگی حقیقی به توزیع فرکانس‌ها داخل کل قطعات موسیقی بستگی دارد؛ اما این محاسبات ساده، ذهنیت مناسبی را از وضعیت واقعی در اختیارمان می‌گذارد.

مقاله‌ی شزم در سال ۲۰۰۳ منتشر شده؛ بنابراین می‌توان نتیجه گرفت که پژوهش‌های مربوط به آن قدیمی‌تر هستند. در سال ۲۰۰۳ پردازنده‌های ۶۴ بیتی به‌صورت عمده وارد بازار شدند. به‌جای استفاده از یک نقطه‌ی لنگر به‌ازای هر منطقه‌ی هدف مانند آنچه در مقاله‌ی شزم پیشنهاد شده است (به‌دلیل ابعاد محدود اعداد صحیح ۳۲ بیتی)، می‌توان ۳ نقطه‌ی لنگر (به‌عنوان مثال ۳ نقطه پیش از منطقه‌ی هدف) استفاده کرده و آدرس هر نقطه در منطقه‌ی هدف را در عدد صحیح ۶۴ بیتی ذخیره کرد. این تغییر می‌تواند زمان جست‌وجو را به‌میزان قابل توجهی کاهش دهد.

در حقیقت جست‌وجو می‌تواند به یافتن ۴ نت داخل موسیقی با فاصله‌های زمانی دلتاـتایم۱، دلتاـتایم۲ و دلتا‌ـ‌تایم۳ باشد؛ بدین مفهوم که تعداد M‌ نتایج می‌تواند بسیار کمتر از آنچه باشد که ما محاسبه کردیم. یکی از مزایای عمده‌ی این جست‌وجوی هویت صوتی در مقیاس‌پذیری وسیع آن است:

• به‌جای داشتن یک دیتابیس هویت صوتی، می‌توان D دیتابیس داشت که هرکدام از آن‌ها 1/D از کل قطعات موسیقی را در بر داشته باشد
• می‌توان به‌صورت همزان در D دیتابیس به‌دنبال موسیقی نزدیک به فایل ضبط‌شده بود
• سپس می‌توان از بین D موسیقی نزدیک‌ترین نمونه را انتخاب کرد
• کل فرآیند می‌تواند D برابر سریع‌تر باشد

یکی دیگر از مباحث به میزان مقاومت الگوریتم در برابر نویز بازمی‌گردد. اگرچه در خصوص این موضوع می‌توان به‌صورت مفصل صحبت کرد؛ اما به‌صورت خلاصه، اگر دقت کرده باشید، در طول این مقاله‌ی بلند‌بالا چندین و چند بار از آستانه‌ها، ضرایب و مقادیر ثابت استفاده کردیم (مانند نرخ نمونه‌برداری، مدت‌زمان فایل ضبط‌شده و...).

همچنین چندین الگوریتم را برای فیلتر یا تولید طیف‌نگاره به‌کار بردیم. تمام این مقادیر ثابت، بر مقاومت در برابر نویز و پیچیدگی زمانی تأثیر می‌گذارند. چالش حقیقی یافتن مقادیر و مناسب و الگوریتم‌هایی است که موارد زیر را به بالاترین حد ممکن خود برسانند:

• مقاومت در برابر نویز
• پیچیدگی زمانی
• دقت (کاهش تعداد نتایج مثبت کاذب)

امیدوارم که در این مرحله، با سازوکار شزم و چگونگی کارکرد آن آشنا شده باشید. مقاله‌ای که مطالعه کردید، شما را به یک متخصص در زمینه‌ی الگوریتم‌های تشخیص موسیقی بدل نمی‌کند؛ اما امیدواریم که اکنون تصویر واضح‌تری از آن در ذهن شما ایجاد شده باشد. به خاطر داشته باشید که شزم تنها یکی از چندین راهکار برای ایجاد هویت صوتی است.

شما اکنون می‌توانید ابزاری را برای تشخیص قطعات موسیقی توسعه دهید. برای انجام چنین کاری توصیه می‌کنیم به این مقاله مراجعه کنید که بر توسعه‌ی نسخه‌ای ساده‌شده از شزم به‌زبان جاوا تمرکز دارد. نویسنده‌ی مقاله‌ی یادشده، در یکی از کنفرانس‌های جاوا صحبت کرده است که اسلاید‌های آن در این لینک در دسترس قرار دارد. شما می‌توانید برای مشاهده‌ی نسخه‌ی MATLAB/Octave شزم، به این لینک نیز مراجعه کنید. در نهایت اینکه به خود مقاله‌ی پژوهشی شزم از بنیان‌گذار این شرکت نیز از این لینک می‌توانید دسترسی داشته باشید.

دنیای محاسبات موسیقایی حوزه‌‌ای بسیار جذاب با الگوریتم‌های پیچیده‌ای است که همه‌روزه بدون اطلاع از سازوکارشان از آن‌ها استفاده می‌کنیم. اگرچه شزم ساده نیست؛ اما درک آن بسیار آسان‌تر از موارد زیر است:

• جست‌وجو از طریق زمزمه: به‌عنوان مثال ساوند‌هاوند، یکی از رقبای شزم به کاربر اجازه می‌دهد تا از طریق زمزمه یا خواندن موسیقی خاصی، آن را بیابد
• تشخیص گفتار و تبدیل متن به گفتار: در اسکایپ، دستیار دیجیتال سیری اپل و OK Google اندروید به‌کار رفته است
• تشابه موسیقی: توانایی شناسایی اینکه دو قطعه‌ی موسیقی مشابه هستند. این الگوریتم توسط Echonest استفاده شده؛ استارتاپی که اخیرا توسط اسپاتیفای تصاحب شده است
• ....

اگر به این مباحث علاقه‌مند باشید، رقابت سالانه‌ای بین پژوهشگران این حوزه برگزار می‌شود و الگوریتم‌های هرکدام از شرکت‌کنندگان در دسترس قرار دارد، شما می‌توانید از طریق این لینک به رقابت MIREX مراجعه کنید.