هر آنچه باید درمورد قوانین نیوتون و حرکت بدانیم

آیزاک نیوتون در ۲۵ دسامبر سال ۱۶۴۳ در وولستروپ انگلیس بهدنیا آمد. این فیزیکدان و ریاضیدان مشهور، آغازگر انقلاب علمی قرن ۱۷ است. در زمینهی اپتیک به کشف ترکیب رنگی نور سفید رسید و بنیانگذار فیزیک اپتیک مدرن شد و در مکانیک کلاسیک، سه قانون حرکت او منجر به تدوین قوانین اصلی و جهانی گرانش شد. در ریاضیات، کاشف اصلی محاسبات ریزمقیاس بوده است. اصول ریاضی فلسفهی طبیعی که در سال ۱۶۸۷ منتشرشد، یکی از مهمترین کارهای او در علم مدرن است.

تاثیرات سازنده
نیوتون در یکی از دهکدههای وولستروپ در یک خانوادهی کشاورز و کارگر بهدنیا آمد. در همان سال، گالیلیو گالیله درگذشت: نیوتون سرانجام میتوانست از ایدههای ریاضی و علمی او استفادهکند و کار گالیله را به سرانجام برساند. زمانی که نیوتون بهدنیا آمد، یک کودک ضعیف و بسیار لاغر بود و حتی امیدی به زندهماندن او در روز اول زندگی نبود و قبل تولد، پدرش را از دست دادهبود. خیلی زود مادرش را هم از دستداد و در طول دو سال دو بار ازدواج کرد.
همسر اولش، نیوتون جوان را با مادربزرگش رها کرد و به همراه یک پسر و دو دختر کوچکش به یکی از روستاهای همسایه رفت. نیوتون تا زمان مرگ بارناباس اسمیت در سال ۱۶۵۳ از مادرش جدا بود و بهدلیل اتفاقاتی که در زندگی تجربه کردهبود و بهدلیل تنفر از ناپدری خود به روانپریشی دچارشد.
زمانی که مادرش برای بار دوم بیوه شد، پسر اولش را مسئول رسیدگی به مسائل خانواده قرار داد. این کار بهزودی به یک فاجعهای برای وضعیت خانواده و همچنین نیوتون تبدیلشد. نیوتون نمیتوانست روی کارهای کشاورزی و رسیدگی به مزرعه و حیوانات تمرکزکند. در بیشتر وقتها، درحال کتابخواندن زیر درختی پیدا میشد. خوشبختانه مادرش به اشتباه خود پیبرد و نیوتون برای آمادهشدن برای دانشگاه، به مدرسهی گرامر درد گرنتام، یعنی همان مدرسهای که قبلا در آن درس میخواند فرستادهشد. نیوتون توانایی بسیار خوبی در ساختن مدلهای مکانیکی مانند ساعت و آسیاب بادی داشت اما بهدلیل وجود اساتید خبره در مدرسهی گرانتام، در تاریخ این مدرسه، نام نیوتون چندان پررنگ نیست.
در مدرسه به سطح خوبی از زبان لاتین رسید ولی دانش او در علم حساب، بسیار سطحی بود. در ژون ۱۶۶۱، آماده بود تا در دانشکدهی ترینیتی دانشگاه کمبریج ثبتنام کند و بهدلیل وقفهای که در روند تحصیلش افتاد، مسنتر از سایر دانشجوها بهنظر میرسید.
اثرات انقلاب علمی
زمانی که در سال ۱۶۶۱ نیوتون وارد کمبریج شد، حرکتی بهنام انقلاب علمی درحال شکلگیری بود و پایههای علم نوین درحال شکلگیری بود. منجمان از کوپرنیک تا کپلر در تلاش بودند تا جهان خورشید مرکز را با جزئیات دقیق توصیفکنند. قبلتر از آن، گالیله مبانی این مکانیک جدید را با توجه به اصل اینرسی (تمایل ماده به حفظ وضعیت حرکت خود یعنی مادهی ساکن میخواهد ساکن بماند و مادهی در حال حرکت میخواهد سرعت یکنواخت خود را حفظ کند) بنیاد نهادهبود.
گروه منجمان آن زمان به رهبری فیلسوف بزرگی بهنام رنه دکارت، فرمولبندی این مکانیک جدید پیچیده و ظریف و لخت (Inert) را آغاز کرد. اما دانشگاههای اروپا از جمله دانشگاه کمبریج، هنوز درگیر فلسفهی از رونق افتادهی ارسطو مبنی بر زمین مرکز بودن جهان بودند و طبیعت را بهصورت کیفی توصیف میکردند و توانایی توصیف کمی آن را نداشتند.
نیوتون مانند هزاران دانشجوی دیگر، تحصیلات عالی خود را با غرقشدن در کار ارسطو آغازکرد. با اینکه فلسفهی جدید، هنوز وارد دروس سیستم آموزشی نشدهبود، همه جا از آن صحبت میشد. نیوتون در مسیر کارهای پژوهشی خود متوجه کارهای رنه دکارت، فیلسوف فرانسوی، و دیگر فیلسوفها در مورد مکانیک شد. این فیلسوفها،برخلاف ارسطو، جهان را متشکل از ذرات ماده میدانستند که درحال حرکت هستند و به واسطهی برهمکنشهای مکانیکی در کنار یکدیگر قرارگرفتهاند.
نیوتون کار علمی خود را در سال ۱۶۶۴ با یک دفترچهی بیاستفاده که قبلا برای تمرینکردن تکالیف مدرسه کنار گذاشتهبود، آغاز کرد. نوشتههایش با عنوان سوالات مسلم در فلسفه شروع میشد. زیر عنوان کار خود جملهای یادداشت کرد و جمله این بود: افلاطون دوست من است. ارسطو دوست من است اما بهترین دوست من، حقیقت است.
سوالاتی که نیوتون یادداشت کرد نشان میداد که او درحال بنیاننهادن چارچوب یک انقلاب علمی است. نیوتون توانست کارهای دکارت را بهخوبی تکمیلکند و با فیلسوف فرانسوی دیگری بهنام پیر گاسندی آشناشود. این فیلسوف بر این عقیده بود که اتمها نیز یک سیستم مکانیکی هستند که طبیعت را توصیف میکنند. شواهد نشان میدهد که نیوتون بهدنبال فلسفهای جذابتر و بهتر از فلسفهی کارتزین بوده است و در این راستا به نتایج خوبی نیز رسیده بود. او توانسته بود وجود ذرات تقسیمناپزیر نهایی را رد کند.
کارهای رابرت بویل شیمیدان در قرن هفدهم، مبانی کار نیوتون در شیمی را فراهم کرد. نیوتون، آثار هنری مور، یکی از پیروان افلاطون در کمبریج، را خواند و با دنیای علم کیمیا و جادو نیز آشنا شد. در آن زمان، علوم و پدیدههای کیمیا و جادو را بهعنوان جهان هرمتیک (Hermetic) میشناختند و پدیدههای طبیعی را کیمیا و جادو توصیف میکردند. در آن زمان، دو بنیاد فکری ریاضیاتی و هرمتیک، روبهروی یکدیگر قرار داشتند. نیوتون، مطالعهی ریاضی را نیز در همین زمان، با آثار دکارت آغاز کرد.
نیوتون، در سال ۱۶۶۹، آمادهی نوشتن یک جمع بندی از کارهای خود بود. او نام اثر خود را " محاسباتی با استفاده از سریهای نامتناهی (On Analysis by Infinite Series)" قرار داد و بهاین وسیله، به فردی شناختهشده تبدیلشد. تا دو سال پس از این رویداد، نیوتون به ریاضیدان مرجع اروپا تبدیلشد و روش جدید محاسبات او متولد شد.
سالهای طاعون
در سال ۱۶۶۵، بهدلیل بیماری طاعون، دانشگاه به مدت دو سال بستهشد. نیوتون ناچارشد بیشتر مدت را در خانه و به مرور آموختههایش بگذراند. نیوتون در این دو سال توانست به محاسبات و یافتههای خود جهت دهد و آنها را در نوشتهای بهنام " از رنگها (of colours)" شرح و بسط دهد. این اثر بیشتر شامل کاربرد ایدههای او در اپتیک است. او در همین مدت زمان در مورد عوامل تاثیرگذرا بر حرکت چرخشی تحقیقکرد و تحلیلها و بررسیهای خود را به حرکت ماه و دیگر سیارات ارتباط داد و قانون عکس مجذوری خورد را نوشت. این قانون به این صورت نوشتهشده است که: نیروی گرانشی وارد بر یک سیاره با عکس مجذور فاصلهی آن از خورشید، نسبت عکس دارد، بعدها این قانون به قانون جهانی گرانش شهرتیافت.
اولین سخنرانی های علمی در ترینیتی
پس از بازشدن دوبارهی دانشگاهها در سال ۱۶۶۷، نیوتون بهعنوان یکی از اعضای دانشکدهی ترینیتی انتخابشد. دو سال بعد، پروفسور ایزاک بارو، مترجم یکی از آثار نیوتون در لندن، از نیوتون برای ارائهی یک سری سخنرانیهای علمی، دعوتکرد. نیوتون، کارهای اخیر خود در زمینهی اپتیک را بهعنوان اولین سخنرانی انتخابکرد.
در طول سه سال بعد (۷۲-۱۶۷۰)، سخنرانیهای نیوتون، اثر کوتاه "از رنگها" را به کتابی با موضوع اپتیک تبدیلکرد.

در سال ۱۶۰۴، اپتیک یکی از موضوعات اصلی در روند انقلاب علمی بود. قانون سینوسی دکارت در مورد ضریب شکست نورهای مختلف، قانون جدیدی را بر ریاضیات نور اعمالکرد و نشانداد که جهان بر پایهی قوانین ریاضی بناشده است. دکارت نور را بهعنوان عنصر اصلی فلسفهی طبیعت در نظرگرفت و ادعاکرد که نور برای انتشار، همواره به یک محیط مادی نیازدارد.
دیدگاه اصلی نیوتون در مورد نور این بود که نوری که در ابتدا سفید بهنظر میرسد، درواقع از رنگهای خاصی تشکیلشده است. دقیقا شبیه پدیدهی رنگینکمان که هنگام بارش باران دیده میشود.
در سالهای ۱۶۶۵ و ۱۶۶۶ آزمایشهایی در مورد نور انجامشد. در این آزمایشها، طیفی از یک باریکهی نور به داخل یک استوانهی تیره تابیده میشود و مشاهدههایی انجام میشود. پس از انجامشدن این آزمایشها، نیوتون، ایدهی ساده و همگن بودن نور را ردکرد. در عوض ادعا کرد که نور ساختاری ترکیبی و ناهمگن دارد و مشاهدهی پدیدهی رنگها از تجزیهی نور ناهمگن و ترکیبی به اجزای سادهی تشکیلدهندهی خود ناشی میشود. با شناختی که نیوتون از طبیعت نور پیداکرده بود، بر این عقیده بود که هرکدام از رنگهای تشکیلدهندهی نور سفید، ویژگیهای منحصر به فردی دارند که از هرکدام آنها به ذرات خاصی از مواد مربوط میشوند. از زمان نیوتون به بعد، ناهمگن بودن نور، پایهی اصلی اپتیک فیزیکی است.

از میزان اثرگذاری تئوری رنگ توصیفشده توسط نیوتون در دانشگاه کمبریج، شواهد مطمئن و کاملا قابل اعتمادی وجودندارد. تئوری رنگ و همچنین کارهای بعدی نیوتون توسط جامعهی سلطنتی لندن که در سال ۱۶۶۰ سازماندادهشد، بهگوش جهان رسید. نیوتون توانستهبود یک تلسکوپ بازتابی طراحیکند و تا قبل از معرفی آن، نام نیوتون برای جامعهی سلطنتی ناشناختهبود. کار نیوتون مورد توجه بسیار قرارگرفت و او در سال ۱۶۷۲، مقالهای در مورد نورها و رنگها نوشت. درکل، مقالهی او بهخوبی در جامعهی علمی پذیرفتهشد اما همزمان، اختلاف نظراتی نیز بهگوش میرسید.
مخالفت های عقیده ای
یکی از مهمترین مخالفان مقالهی نیوتون، رابرت هوک بود. رابرت هوک یکی از رهبران جامعهی سلطنتی بود و خود را استاد اپتیک میدانست. آتش خشم عمومی بر ضد هوک برانگیختهشد و این واقعه بسیار بعید و غیر منتظره بود. نیوتون نتوانست از انتقادات و مخالفتها در امان بماند و یک سال پس از انتشار مقاله با مخالفتها و مباحثههای زیادی روبهرو شد و به گوشهگیر شد.
در سال ۱۶۷۵، در طول سفری به لندن، شایعهی پذیرفتهشدن تئوری رنگ نیوتون توسط هوک بهگوش نیوتون رسید. بنابراین او توانست جسورانه مقالهی دوم خود را در مورد آزمایش پدیدهی رنگها با استفاده از فیلمهای نازک را بنویسد. هدف این مقاله، توصیف رنگ اجسام جامد بود. بهاین وسیله علاوهبر شکست نور، با پدیدهی بازتاب نیز میتوان نشانداد که نور سفید از اجزای دیگری تشکیلشده است. توضیح نیوتون در مورد رنگ اجسام، موفق نبود اما مقالهی او برای اولین بار نشانداد که پدیدههای اپتیکی دورهای وجود دارند.
نیوتون در آزمایشی که به آزمایش حلقههای نیوتون شهرت دارد، حلقههای متمرکزی از نور را بین لنز و یک شیشهی نازک مشاهده کرد. فاصلهی بین این حلقهها به قطر لایهی هوا بستگیدارد.
قانون جهانی گرانش نیوتون
جهان میداند که افتادن یک سیب از درخت، منجر به نوشتهشدن قانون جهانی گرانش توسط نیوتون شد. افتادن سیب، نیوتون را به فکر فروبرد. او از خود پرسید که چرا سیب به سمت بالا یا اطراف پرتاب نشد و مستقیما بهسمت زمین سقوط کرد. او با خود فکرکرد که شاید واقعا زمین در افتادن سیب موثر است و سپس بهدنبال کشف چگونگی این تاثیر، شب و روز خود را وقفکرد.
تئوری نیوتون بهصورت زیر نوشتهشده است:
این تئوری برای دو جسم نوشتهشده است. نیروی گرانش بین این دو جسم با افزایش فاصلهی این دو جسم از یکدیگر کاهش پیدا میکند. علاوهبر این، شدت این نیرو، با افزایش جرم هرکدام از اجسام موردنظر، افزایش مییابد. برای مثالی از دو جسم، زمین و ماه را درنظر بگیرید. همین نیروی گرانش بین زمین و ماه است که ماه را در مدار دایرهای به دور زمین نگهداشته است.
نیروی گرانش بین این دو جسم با افزایش فاصلهی این دو جسم از یکدیگر کاهش پیدا میکند
قانون جهانی گرانش نیوتون بیان میکند که تر جسم نقطهای (منظور از جسم نقطهای، هر جسم مادی دارای جرم و به هر ابعادی است) به جسم نقطهای دیگر، نیروی گرانش وارد میکند که جهت این نیرو، در راستای خط واصل بین دو جسم نقطهای است. این قانون شامل همهی اجسام مادی کوچک و بزرگ میشود. اگر دو جسم بزرگ را در نظر بگیریم که بهطور خاص، شکل تقریبا کروی نیز داشتهباشند، کل جرم هرکدام از این کرهها را میتوانیم بهصورت یک نقطهی متمرکز در مرکز آن درنظر بگیریم. علاوهبر این اگر این دو جسم به میزان زیادی از یکدیگر دور شوند، از این فاصله بهصورت نقطهای دیده میشوند.
با اینکه نیوتون توانست قانون جهانی گرانش خود را بنویسد و بهصورت آزمایشی آن را اثباتکند، همچنان نمیتوانست نیروی گرانش بین دو جسم را نسبت به نیروی گرانش بین دو جسم دیگر محاسبهکند. تا اینکه هنری کاوندیش توانست درستی ثابت گرانش (G) مورد محاسبهی خود را به برساند. پس از آن، فرم جبری گرانش جهانی نوشتهشد.
با اینکه بیشتر اجسام موجود در جهان، متقارن نیستند، برای نوشتن قانون گرانش برای هرکدام از آنها، باید آنها را بهصورت جسم نقطهای در نظر بگیریم. برای اجسام تقریبا متقارن و کروی، این کار آسان است.
گرانش جهانی برای اجسام متقارن کروی
قانون جهانی گرانش برای دو جسم نقطهای بیان میکند که: نیروی گرانش بین این دو جسم، با اندازهی جرم آنها نسبت مستقیم و با مربع فاصلهی آنها از یکدیگر(d) نسبت عکس دارد.
F=GmM/d2
در رابطهی بالا، F نیروی گرانش بین دو جسم به جرمهای m و M است که با فاصلهی d از یکدیگر قرار دارند.
با این وجود، بیشتر اجسام، کروی نیستند و برای محاسبهی نیروی گرانش بین دو جسم سهبعدی، باید آنها را با یک نقطه در فضا مشخصکرد و جرم آنها را در یک نقطه بهنام مرکز جرم، متمرکز در نظر گرفت.
نظریه ی پوسته
نیوتون نظریهی پوسته را به اثبات رساند. این نظریه بیان میکند که:
۱- رفتار گرانشی یک جسم کروی در مقابل اجسام دیگر بهگونهای است که بهنظر میرسد تمام جرم آن در مرکزش متمرکز شدهاست.
۲- اگر جسمی درون یک جسم دیگر متقارن کروی قرار بگیرد، نیروی گرانشی خالصی از طرف جسم متقارن بیرونی به آن وارد نمیشود.
از آنجایی که نیرو یک کمیت برداری است، نیروی خالص وارد بر یک جسم از طرف تمامی قسمتهای یک پوستهی کروی، برابر با نیرویی است که از طرف مرکز جرم (Center Of Mass) پوسته یعنی نقطهی میانی پوستهی کروی به جسم موردنظر وارد میشود. بنابراین زمانی که میخواهیم نیروی گرانش وارد بر یک توپ ۱۰ کیلوگرمی را محاسبهکنیم، فاصلهی زمین تا توپ، همان فاصلهی مرکز جرم توپ تا مرکز جرم زمین است.
میتوانیم یک کره را به تعداد بسیار زیادی پوستهی کروی نازک و هممرکز (درست مثل ساختار پوستهای یک پیاز) تقسیمکنیم. بنابر تئوری پوستهای، نیروی گرانش وارد بر نقطهای از داخل یک جسم کروی، از طرف همان جسم، برابر با نیرویی است که داخل همان حجم با همان شعاع مورد نظر قرار دارد. بهعبارت دیگر، اگر برای مثال شعاع جسم کروی ۱۰ متر باشد و ما نیروی گرانش وارد بر نقطهای به شعاع ۸ متر از همان جسم را بخواهیم، تنها باید جرم داخلی کرهای به شعاع ۸ متر را داشتهباشیم و بقیهی جرم برای ما اهمیتی ندارد.
زمانی که بخواهیم نیروی گرانشی وارد بر نقطهای در خارج با داخل یک جسم کروی به شعاع R را محاسبهکنیم، تنها دو حالت ساده در این مورد وجود دارد که باید بررسی کنیم: اولین مورد، یک پوستهی کروی توخالی است و مورد دیگر، یک کرهی همگن توپر است.
مورد اول: پوستهی کروی توخالی
نیروی گرانش وارد بر یک نقطه داخل پوستهی کروی از طرف همین پوسته، برابر است با جمع نیروهایی که تک تک اجزای پوسته به نقطهی مورد نظر وارد میکنند و در نهایت، جمع همهی این نیروها برابر صفر است. به معنی که جرم m واقع در پوستهی کروی توخالی به جرم M، هیچ نیروی خالصی از طرف پوسته احساس نمیکند.
نیروی وارد بر یک جسم خارج از پوستهی کروی به جرم M، از جمع برداری نیرویی وارد از طرف تک تک اجزای کره بهدست میآید. حاصل این جمع، یک نیروی خالص است که برابر با نیروی واردشده از طرف مرکز جرم پوسته به جسم خارج آن است.
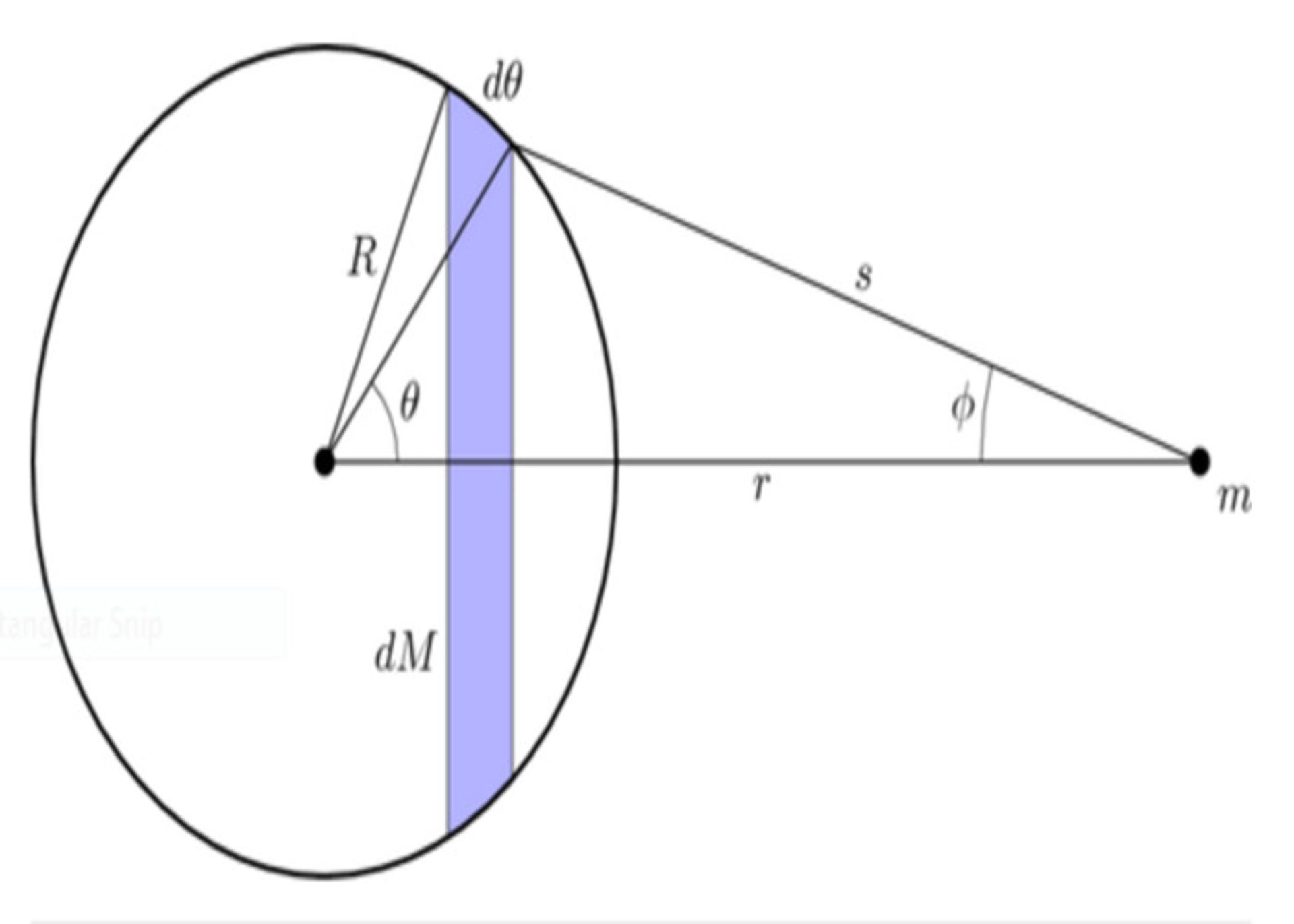
از این شکل برای اثبات نظریهی پوسته استفاده شده است: در این مورد، یک پوستهی کروی به جرم M (سمت چپ تصویر) به جرم کوچک m (سمت راست تصویر) خارج پوسته، نیرو وارد میکند. در این شکل، مساحت سطحی قسمت کوچکی از کره با رنگ آبی نشان دادهشده است.
مورد دوم: کرهی جامد و همگن توپر
مورد دومی که بررسی میکنیم یک کرهی جامد و همگن به جرم M و شعاع R است که جسمی به جرم m به فاصلهی d از مرکز آن قرار گرفته است و dRاست. میتوانیم از نتایج این نظریه برای تحلیل این مورد استفاده کنیم. پوستههای متوالی تشکیلدهندهی کره که در شعاعهای بیشتر از d قرار دارند، قابل چشمپوشی هستند و در محاسبهی نیروی وارد بر جرمی در فاصلهی d از مرکز کره تاثیری ندارند و تنها جرم داخل کرهای به شعاع d، یعنی Md را درنظر میگیریم. از طرف دیگر، جرم کرهای بهشعاع d در نقطهی مرکزی آن متمرکز درنظر گرفته میشود. بنابراین، نیروی گرانش وارد بر جرم m بهصورت زیر محاسبه میشود:
F=GmM/d^2
دقیقا شبیه مورد پوستهی کروی توخالی، نیروی وارد بر جسمی به جرم m خارج از کرهی همگن توپر، از جمع برداری نیروی تک تک پوستههای تشکیلدهندهی کره محاسبه میشود. این نیرو بهگونهای عمل میکند که گویا کل جرم کره در مرکز آن متمرکز است.
وزن زمین
در مورد اجسامی که گستردگی فضایی دارند، نیروی گرانش وارد بر این جسم، از جمع نیروهای وارد بر تک تک نقاط تشکیلدهندهی این جسم بهدست میآید.
قانون جهانی گرانش نیوتون نشان میدهد که هر جسم نقطهای در جهان، به جسم نقطهای دیگر نیرو وارد میکند و این نیرو با مجذور فاصلهی دو جسم، نسبت عکس و با جرم دو جسم نسبت مستقیم دارد.
قانون گرانش به زبان جدید بهاین صورت بیان میشود که:
هر جرم نقطهای، جرم نقطهای دیگر را با نیرویی در راستای خط واصل دو جرم بهخود جذب میکند.
برای نقاط داخل یک ساختار کروی، میتوان برای یافتن نیروی گرانشی از نظریهی پوستهی نیوتون استفادهکرد. همانگونه که در بالا توضیح داده شد، این نظریه، چگونگی تاثیر گرانشی سایر نقاط را بر نقطهای واقع در فاصلهی r0 از مرکز کره را به ما نشان میدهد.
در نتیجهی این نظریه، در مورد یک پوستهی کروی همگن، نیروی گرانشی داخل پوسته، تغییراتی ندارد و در همهی نقاط یکسان است. علاوهبر این، در یک کرهی توپر یکنواخت، نیروی گرانش، با افزایش فاصله از مرکز کره، بهصورت خطی افزایش مییابد. افزایش نیروی ناشی از افزایش جرم موثر، ۱.۵ برابر از کاهش نیروی ناشی از افزایش فاصله، بیشتر است. بنابراین در کل، در این مورد، با افزایش فاصله از مرکز، نیرو افزایش مییابد.
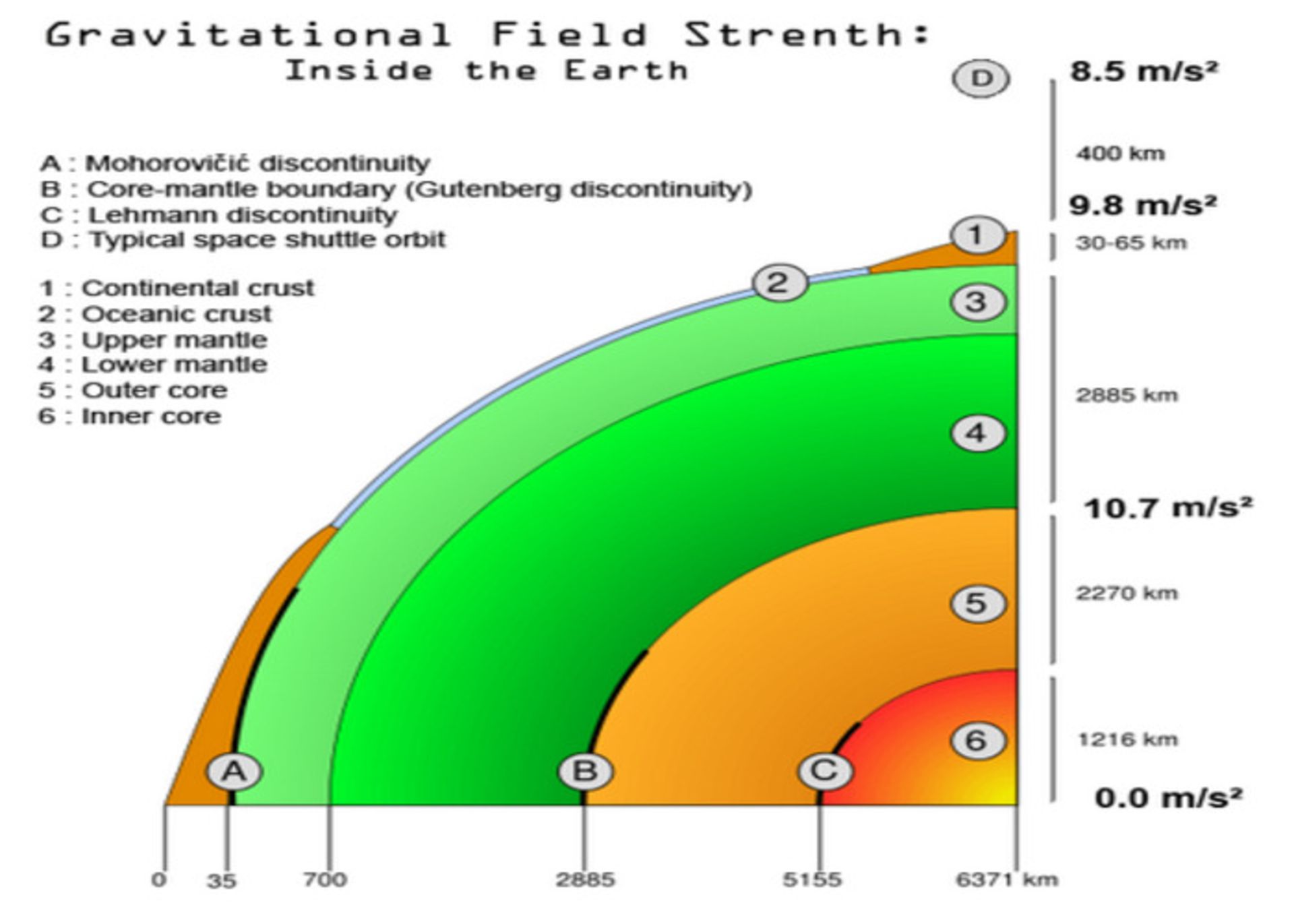
علاوهبر این، اگر کرهای را در نظر بگیریم که دارای یک هستهی همگن باشد و بدنه و پوستهی آن نیز همگن بوده و چگالی آن از ۲۳ چگالی هسته کمتر باشد، در این صورت، در ابتدا گرانش از مرکز کره به سمت پوسته افزایش مییابد. در صورتی که کره به اندازهی کافی بزرگ باشد، زمانی که بیشتر از مرکز دور شویم، گرانش دوباره افزایش مییابد و در نهایت، نیروی گرانش در هسته و پوسته بیشترین مقدار را دارد.
نیروی گرانش زمین در هسته و پوستهی آن میتواند بیشتر از مقدار نشان داده شده در عکس زیر باشد:
قوانین حرکت نیوتون
موضوعی که همیشه در علم مکانیک و حرکت بررسی میشود، چگونگی حرکت اجسام است. در مورد هر جسم در حال حرکت، میتوان با داشتن اطلاعات اولیهی جسم از جمله، سرعت اولیهی آن، چگونگی حرکت آن در لحظات بعدی را پیشبینی کرد. اما موضوع مهمی که باید به آن توجه کنیم، نیروها هستند. برای آشنایی بهتر با آنها و چگونگی تاثیر آنها بر حرکت اجسام، به قوانین حرکت نیوتون مراجعه میکنیم.
نیوتون قوانین سهگانهی خود را در سال ۱۶۸۷ با انتشار کتاب Principia به جهان معرفیکرد. امروزه یعنی حدود سیصد سال پس از نیوتون، قوانین حرکت نیوتون را به تمام اجسام کلاسیکی درحال حرکت اعمال میکنیم.
قانون اول نیوتون
قانون اول نیوتون به قانون اینرسی یا لختی شهرت دارد و بهطور کلی بیان میکند که هر جسمی تمایل دارد حالت خود را تا ابد حفظ کند. بهعبارت دیگر، جسم درحال حرکت، به حرکت خود ادامه میدهد و جسم ساکن، ساکن باقی میماند تا اینکه هرکدام از آنها تحت تاثیر نیرویی قرار بگیرند. در این صورت امکان تغییر حالت حرکتی بهوجود میآید.
راه دیگر بیان این قانون این است که برای تغییر وضعیت حرکت جسم و دادن شتاب به جسم، به نیروی خالص نیاز داریم. برای اندازهگیری اینرسی، مهمترین کمیتی که باید به آن توجه کنیم، جرم است.
برای درک اهمیت جرم، یک توپ پلاستیکی و یک توپ بولینگ را تصور کنید. بهحرکت در آوردن توپ بولینگ، بسیار مشکلتر از بهحرکت درآوردن توپ پلاستیکی است و بههمین ترتیب سختتر میتوانیم یک توپ بولینگ را نسبت به یک توپ پلاستیکی از بهحال سکون در آوریم. توپ بولینگ بهدلیل داشتن جرم بیشتر، اینرسی بیشتری نیز نسبت به توپ پلاستیکی دارد.

جرم بیشتر به معنی مادهی بیشتر است و این یعنی به نیروی بیشتری برای تغییر حرکت قبلی جسمی با جرم بیشتر احتیاج داریم. این ایده کاملا با قانون دوم نیوتون هماهنگ است.
قانون دوم نیوتون
نیروی خالص وارد بر یک جسم، برابر است با جرم جسم در شتاب آن:
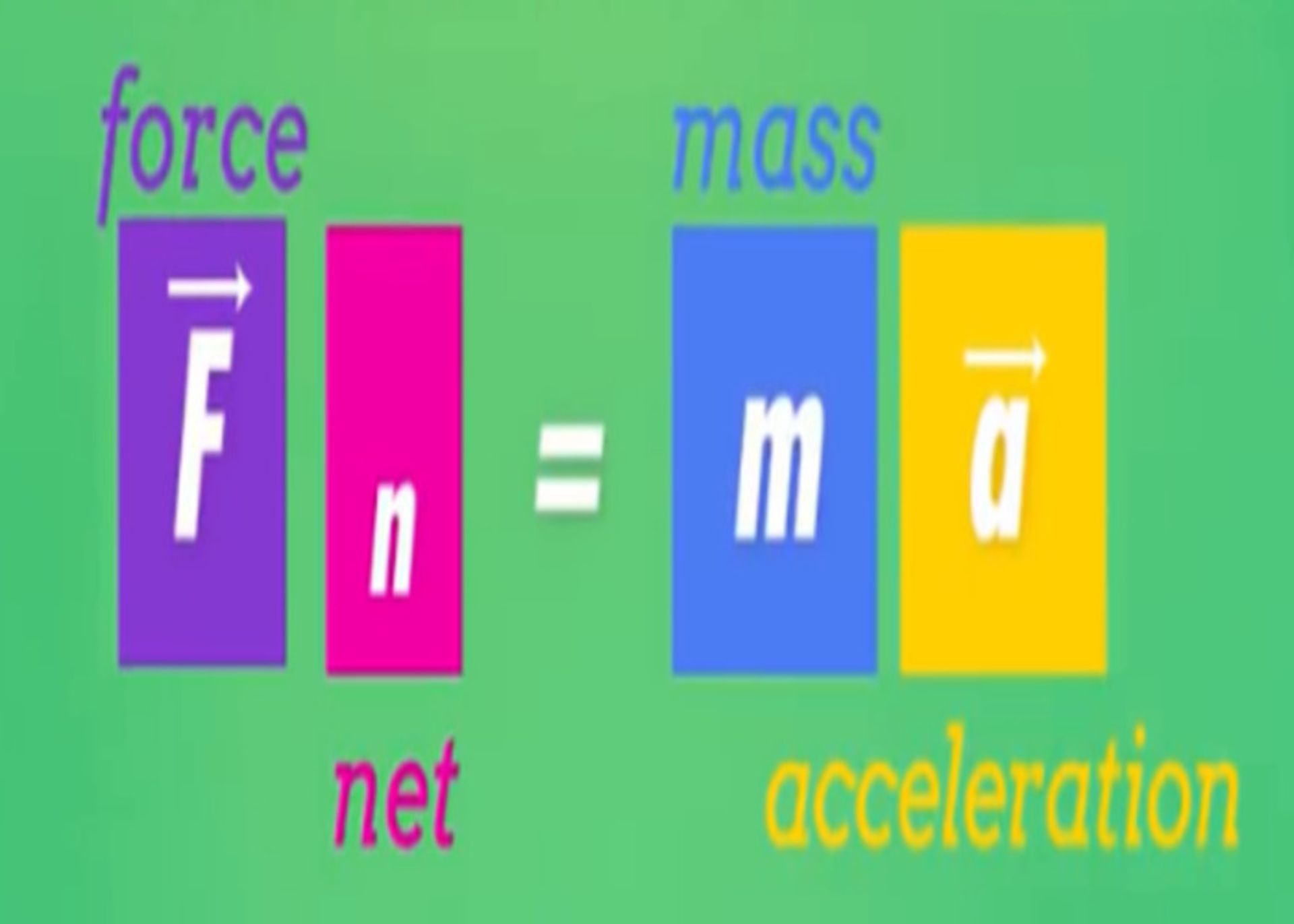
توجه داشته باشید که در اینجا تنها نیروی خالص وارد بر یک جسم را درنظر داریم. به این معنی که باید تمامی نیروهای وارد بر جسم را درنظر بگیریم، آنها را با استفاده از قوانین جمع برداری با یکدیگر جمع بزنیم و سپس حاصل جمع تمامی این نیروها، نیروی خالص را به ما میدهد.
برای درک بهتر این موضوع، یک زمین هاکی تقریبا بدون اصطکاک را درنظر بگیرید. فردی به دیسک هاکی ضربه میزند و بهدلیل نبود هیچگونه نیروی بازدارنده (نیروی اصطکاک)، دیسک به حرکت خود ادامه میدهد تا نیرویی مانع حرکتش شود. این نیرو میتواند دروازه بان باشد. زمانی که دیسک از حرکت میایستد، نیروی خالص وارد بر آن صفر است. بهعبارت دیگر، تمام نیروهای وارد بر دیسک در تمام جهتها، یکدیگر را خنثی میکنند. به این حالت، تعادل گفته میشود.

یک جسم، در حالت تعادل میتواند همچنان درحال حرکت نیز باشد اما سرعت آن تغییری نمیکند و شتاب ندارد. بنابراین، باز هم نیروی خالص وارد بر آن، صفر خواهدبود.
یکی از متداولترین نیروهایی که میتواند اجسام را وادار به حرکت کند، نیروی گرانش است. فرضکنید یک توپ پنج کیلوگرمی را مستقیما به هوا پرتاب میکنیم. در این شرایط، توپ تا نقطهای بالا رفته و سپس بهسمت زمین برمیگردد. در این شرایط، توپ با شتاب گرانشی زمین یعنی با شتاب ۹.۸۱m/s2حرکت میکند. از آنجایی که نیرو برابر با جرم در شتاب است، بهراحتی میتوانیم نیروی گرانش وارد بر توپ از طرف زمین را محاسبه کنیم. این نیرو، بهعنوان نیروی وزن شناخته میشود.
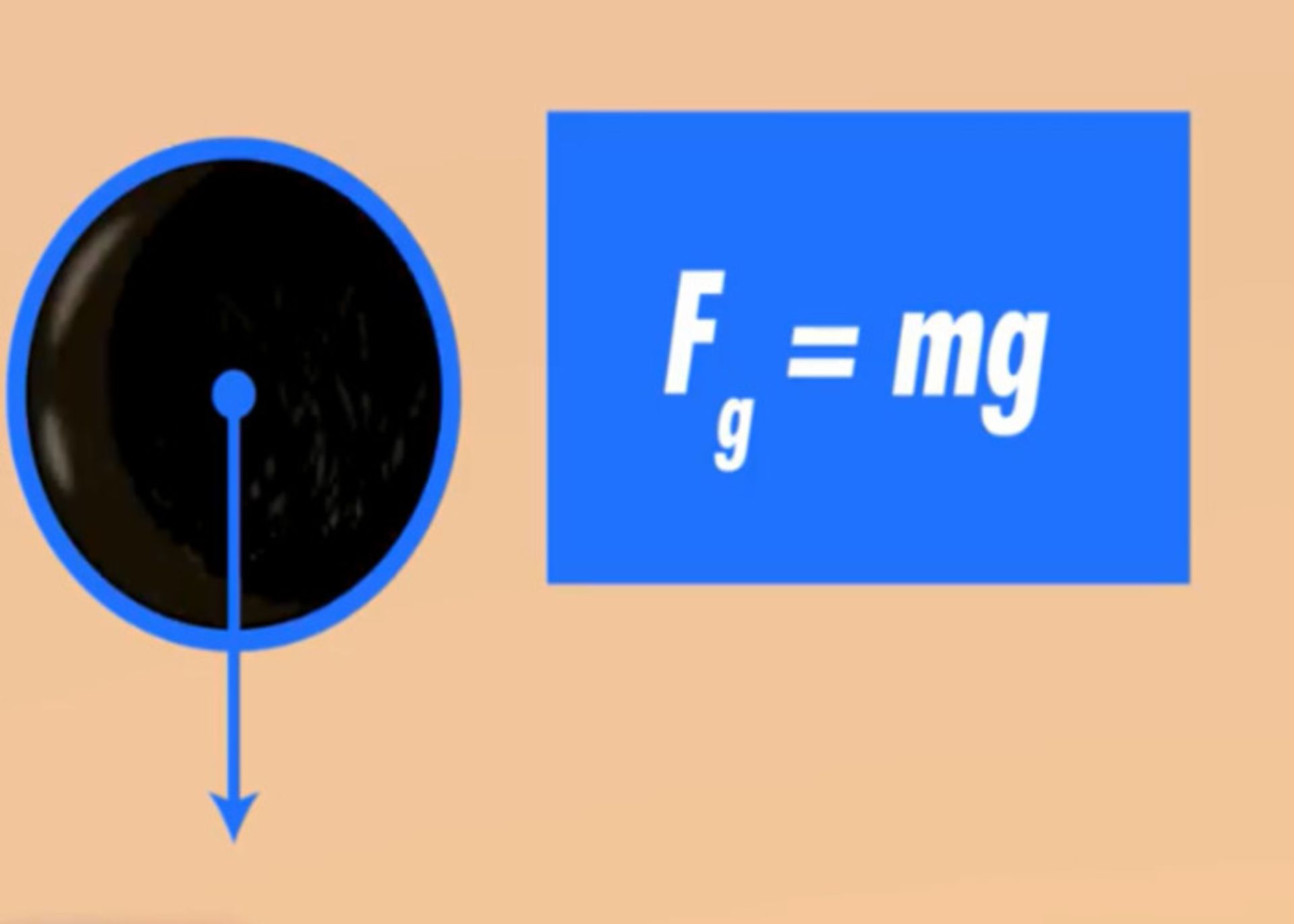
به افتخار نیوتون، واحد نیرو یعنی کیلوگرم در متر بر مجذور ثانیه (Kg.ms^2)، نیوتون نامیده میشود. توجه داشته باشید که واحد نیرو، حتی نیروی وزن، کیلوگرم نیست، نیوتون است. کیلوگرم تنها واحد جرم است. زمانی که جرم جسمی را در شتاب گرانش زمین یعنی g ضربکنیم، میتوانیم نیروی وزن را محاسبه کنیم.
گرانش تنها نیروی تاثیرگذار بر یک جسم نیست. برای محاسبهی نیروی خالص وارد بر یک جسم، باید نیروهای دیگر را نیز درنظر بگیریم. این موضوع ما را به قانون سوم میرساند.
قانون سوم نیوتون
این قانون بیان میکند که: هر عملی عکسالعملی دارد که اندازهی آن با اندازهی نیروی واردشده برابر است و جهت آن، مخالف جهت نیروی واردشده است. بهعبارت دیگر، اگر به جسمی نیرو وارد کنیم، جسم هم همان نیرو را به ما وارد میکند. این موضوع در مورد نیروی نرمال درست است. منظور از نیروی نرمال، نیروی عمود بر سطح تکیهگاه جسم است.
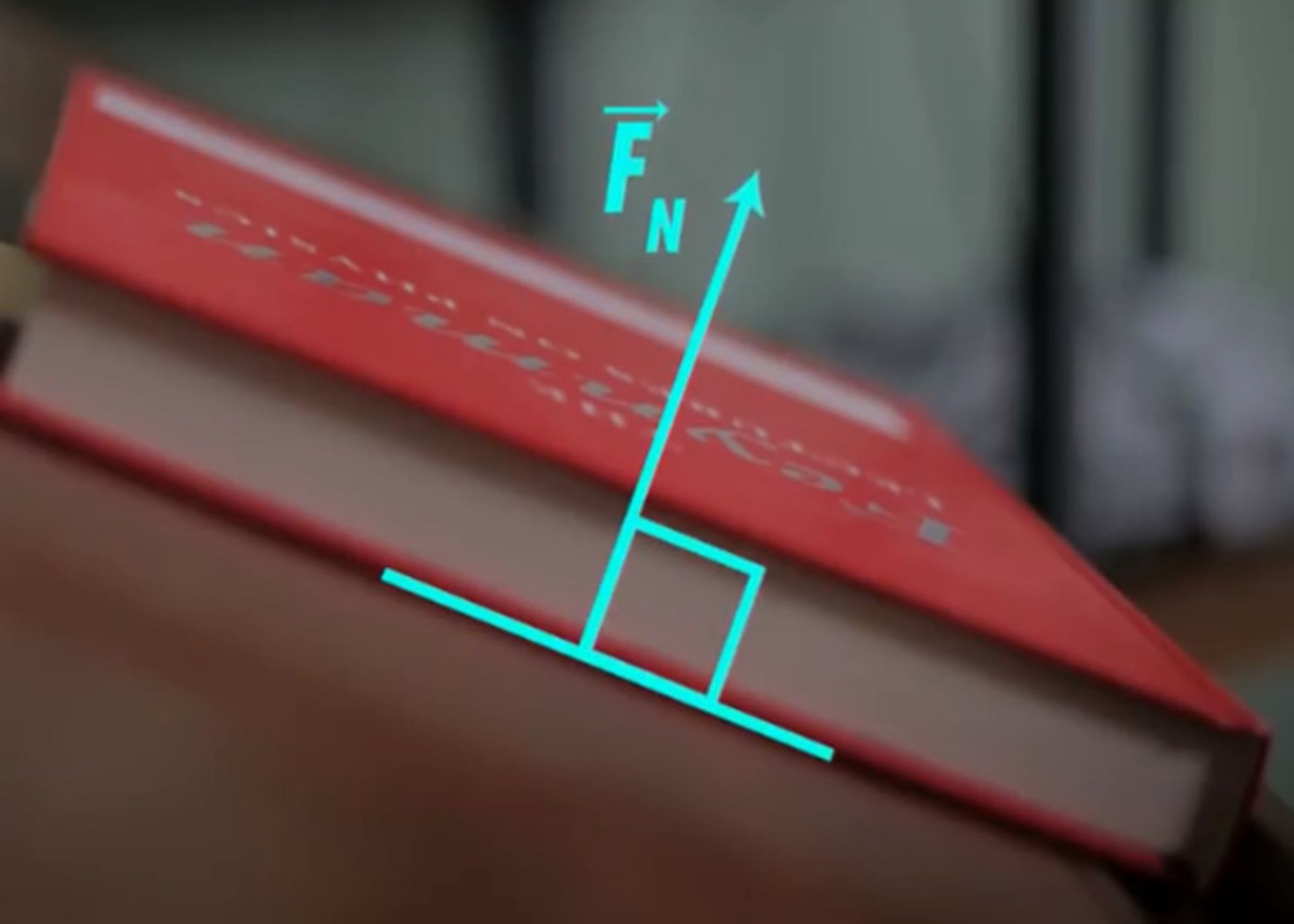
برای مثال اگر کتابی را روی میز قراردهیم، از طرف سطح میز نیروی نرمال بهسمت بالا بر این کتاب وارد میشود. اگر همین کتاب را روی سطح شیبدار قرار دهیم، باز هم نیروی نرمال بر سطح شیبدار عمود است.

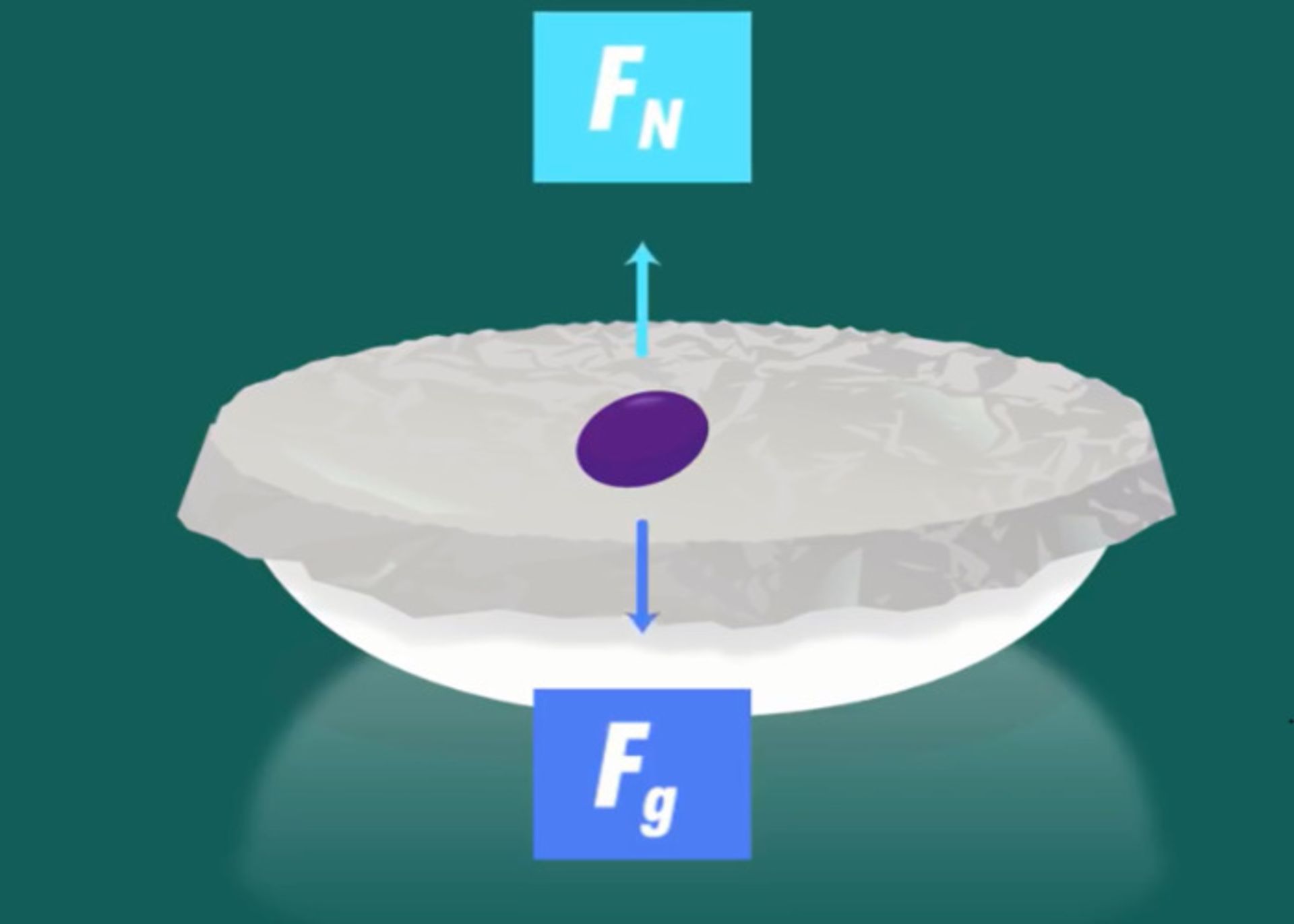
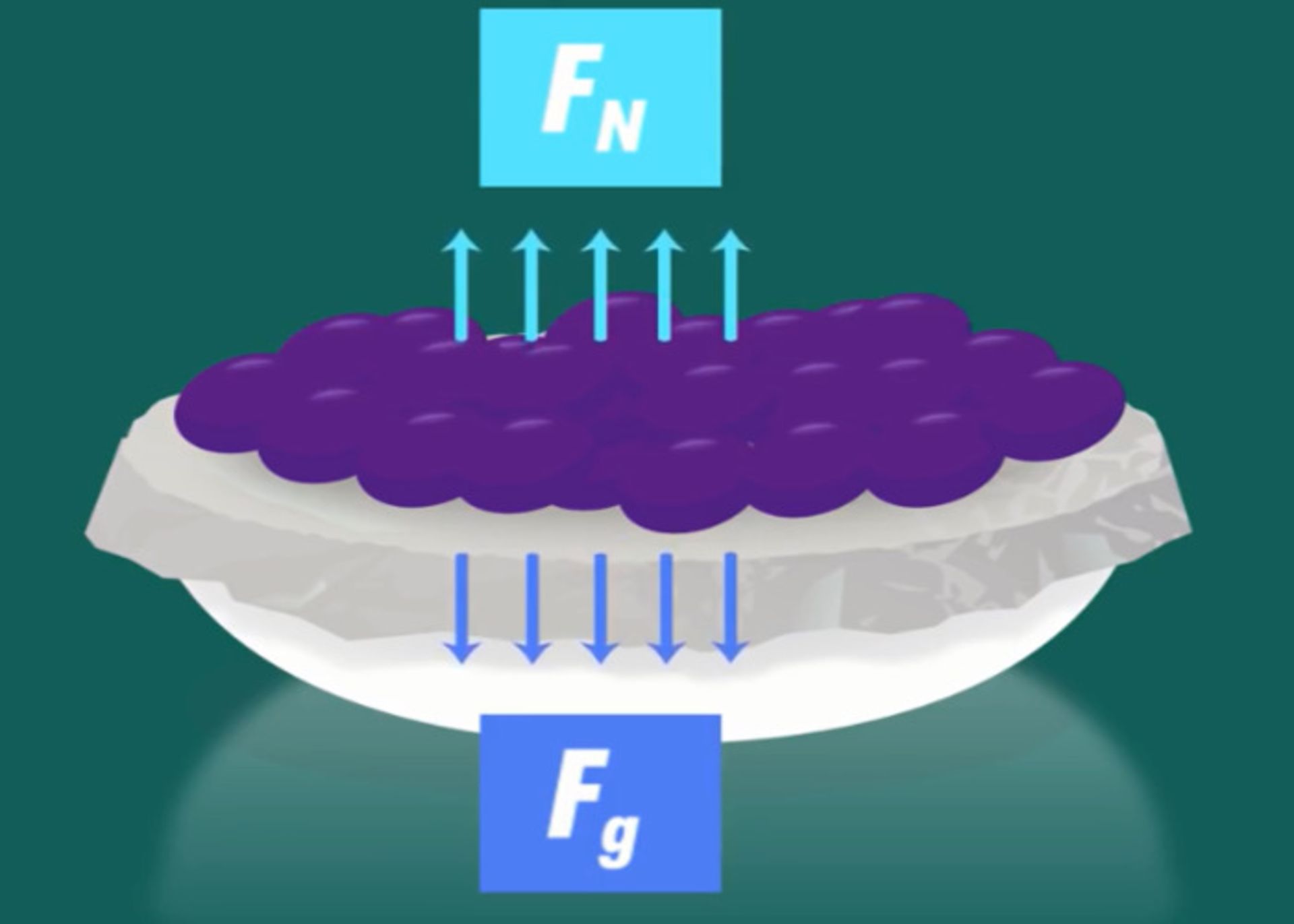
در شرایط تعادل، همیشه نیروی نرمال یا نیروی عمودی سطح، با نیروهای مقابل خود برابر است. ظرفی را تصور کنید که یک درپوش نایلونی آن را پوشانده است. اگر یک سنگ کوچک روی این درپوش قراردهیم، نیروی عمودی سطح با نیروی وزن این سنگ برابر است. اگر تعداد سنگها را افزایشدهیم، نیروی عمودی سطح نیز متناسب با وزن سنگها تغییر میکند. تا جایی که نایلون دیگر تحمل وزن سنگها را ندارد و سنگها سقوط میکنند.
اما قانون سوم نیوتون دقیقا چه میگوید؟ زمانی که انگشتمان را به میز فشار میدهیم، میز نیز همان نیرو را به انگشت ما وارد میکند و ما میتوانیم این نیرو را احساسکنیم. پس سوال اینجاست که چگونه میتوانیم اجسام را به حرکت درآوریم؟
زمانی که یک گوزن، کالسکه را بهسمت جلو میکشد، کالسکه نیز بههمان اندازه به گوزن نیرو واردکرده و آن را بهسمت عقب میکشد. اما میدانیم که باز هم کالسکه بهسمت جلو حرکت میکند. زمانی که گوزن روی زمین قدم برمیدارد، نیرویی بهسمت عقب به زمین وارد میکند و زمین نیز همین نیرو را بهسمت جلو به گوزن وارد میکند. از طرفی، گوزن، طناب کالسکه را بهسمت جلو میکشد و بنابراین، طناب نیز گوزن را بهسمت عقب میکشد. اما نکته اینجاست که نیرویی که زمین بهسمت جلو به گوزن وارد میکند، بیشتر از نیروی بهسمت عقب طناب است و بنابراین، کالسکه همراه گوزن بهسمت جلو حرکت میکند. بنا براین، بدون فیزیک، کریسمسی هم وجود نداشت.

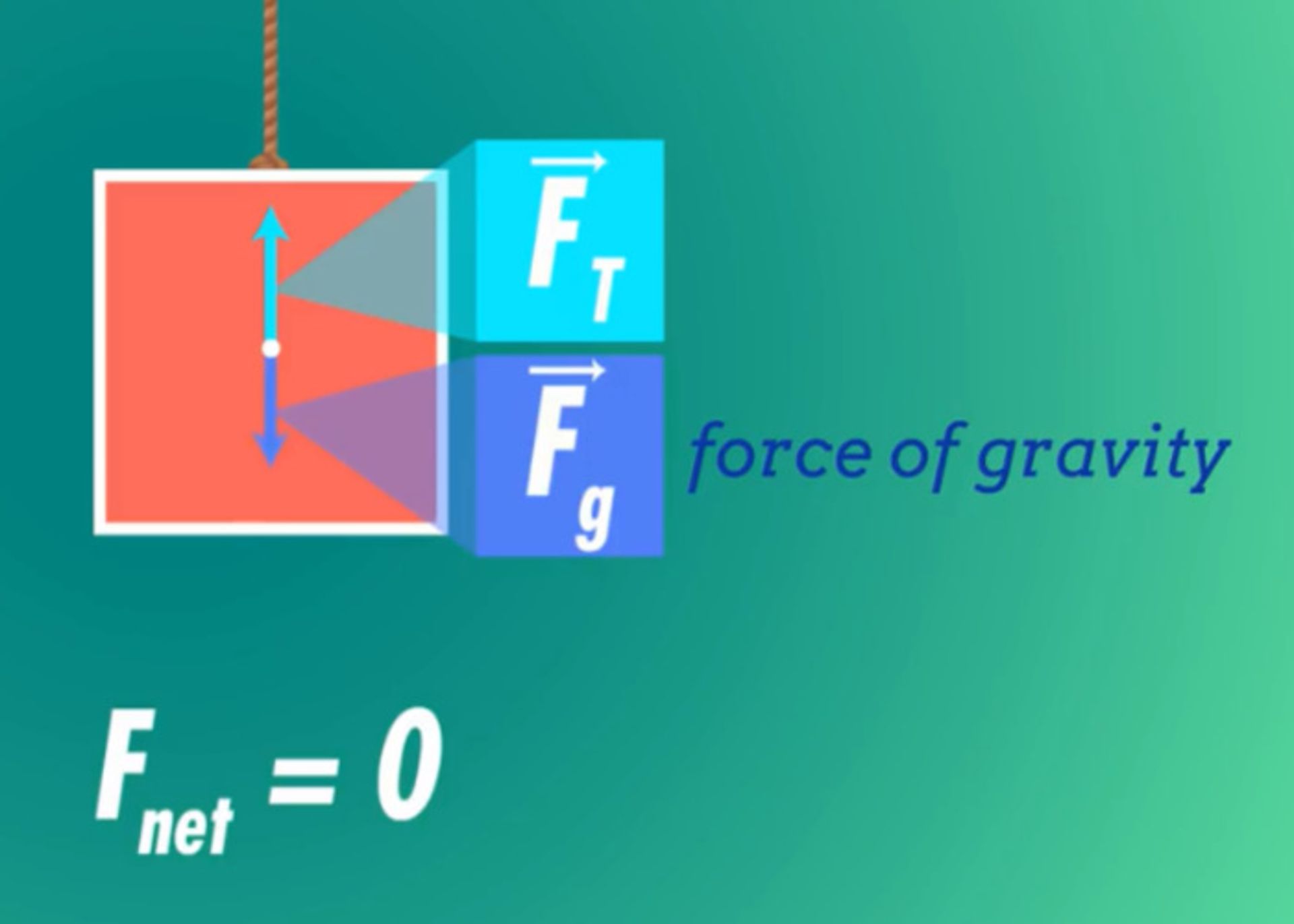
فرض کنید جعبهای را با طناب از سقف آویزان کردهایم. در این حالت، نیروی طناب با نیروی وزن جعبه برابر است و بهدلیل ساکن بودن جعبه، نیروی خالص وارد بر جعبه صفر است. هرچه جرم جعبه و در نتیجهی آن نیروی وزن جعبه بیشتر شود، نیروی طناب نیز متناسب با همین نیرو،بیشتر میشود.
در شرایط دیگر، فرضکنید که درون یک آسانسور هستید و جرم آسانسور ۱۰۰۰ کیلوگرم است. آسانسور از سمت دیگر به یک وزنهی ۸۵۰ کیلوگرمی متصل است. بهدلیل بیشتر بودن جرم آسانسور از جرم وزنه، مسلما آسانسور بهسمت پایین حرکت میکند اما شتاب این حرکت چقدر است؟ و آیا این آسانسور امنیت لازم را دارد؟
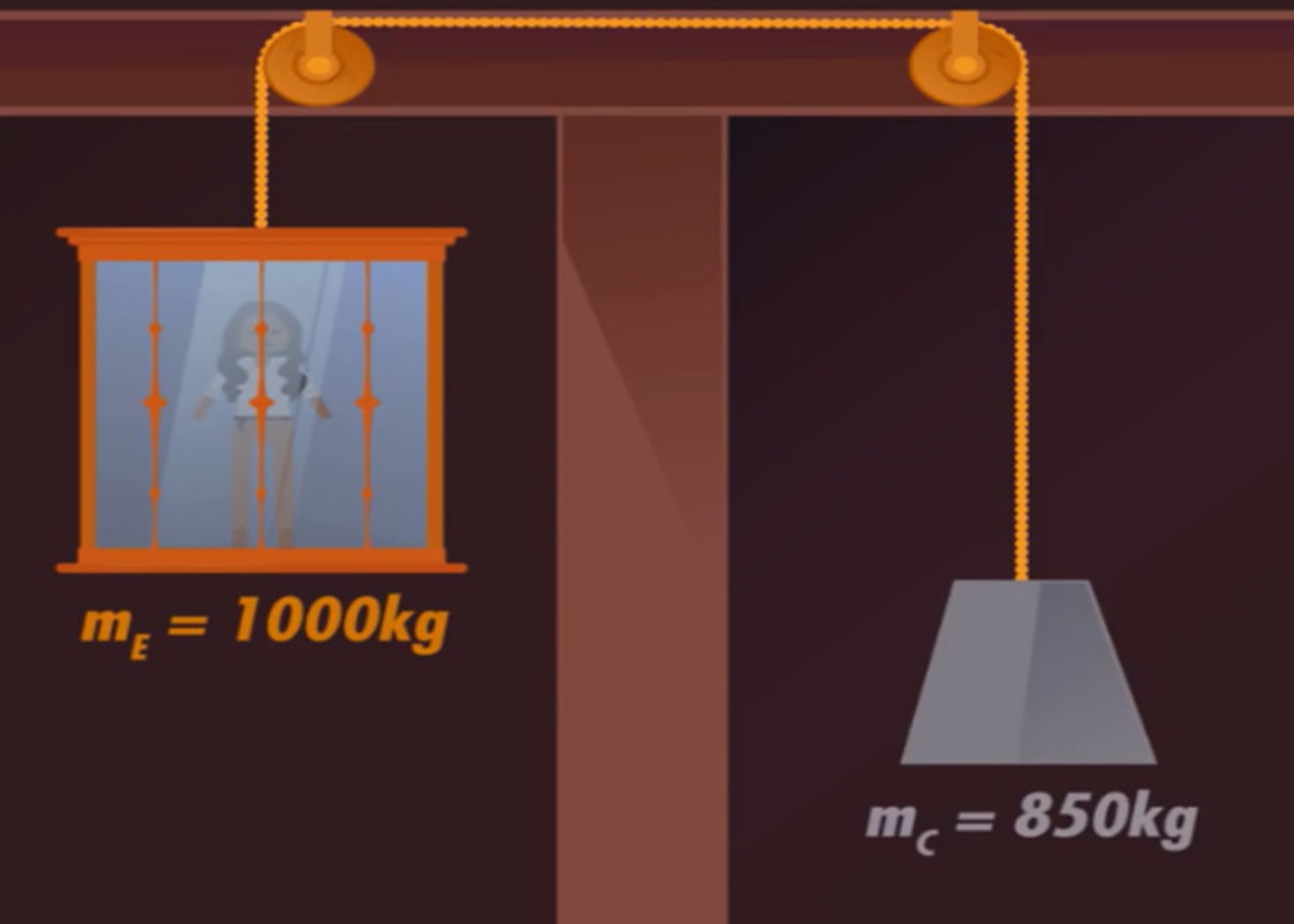
برای محاسبهی شتاب حرکت، برای آسانسور و وزنه بهصورت جداگانه برآیند نیروها را مینویسیم و در این محاسبات، جهت بالا را مثبت درنظر میگیریم. در این صورت، معادلهی نیرو برای آسانسور بهشکل زیر است:

بههمین صورت، معادلهی نیرو برای وزنه را نیز مینویسیم:
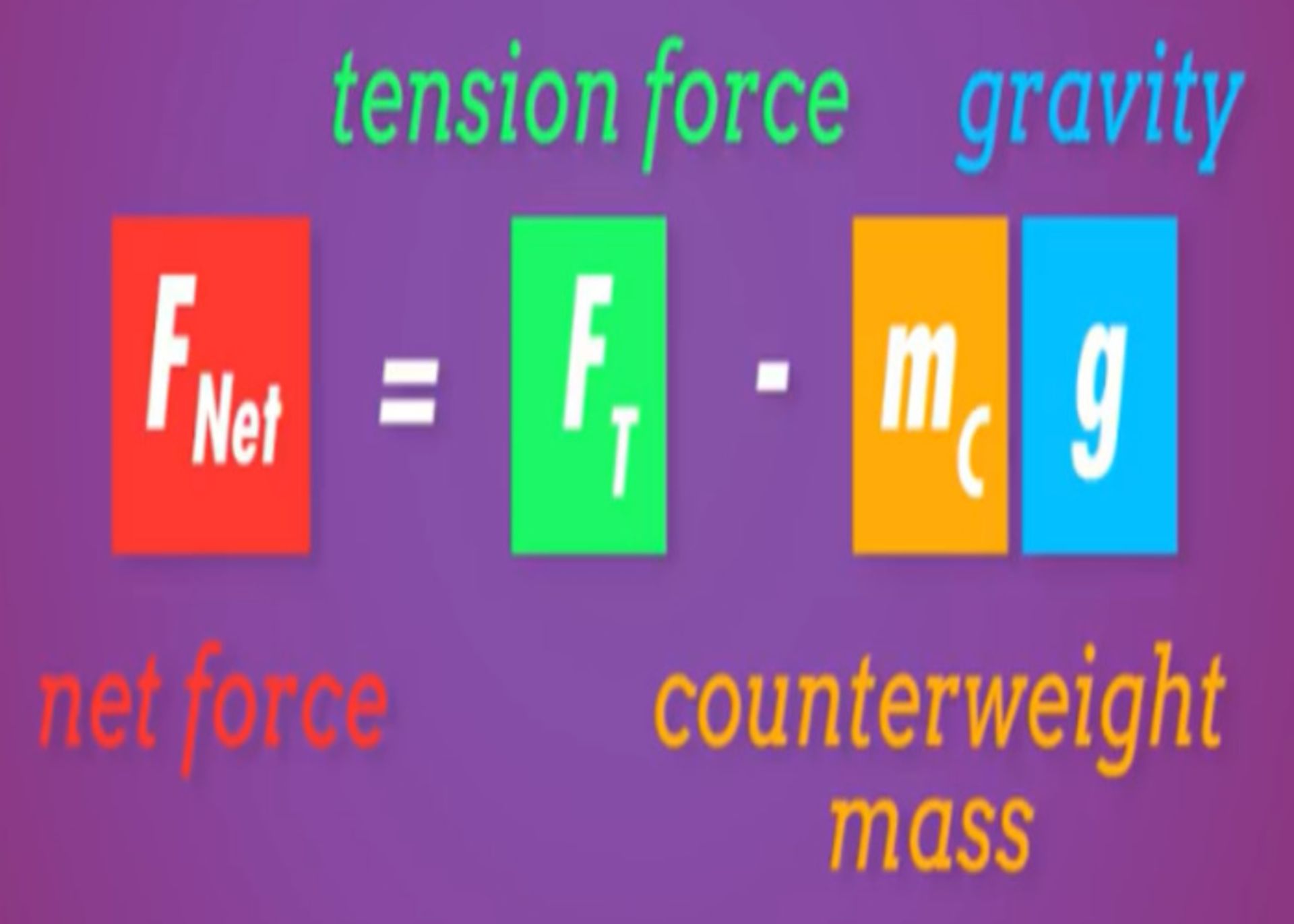
طبق قانون دوم نیوتون، هرکدام از این معادلات برابر با جرم در شتاب هستند و شتاب وزنه و آسانسور نیز با هم برابر است. بنابراین، به این صورت میتوانیم شتاب مجموعه را محاسبهکنیم.
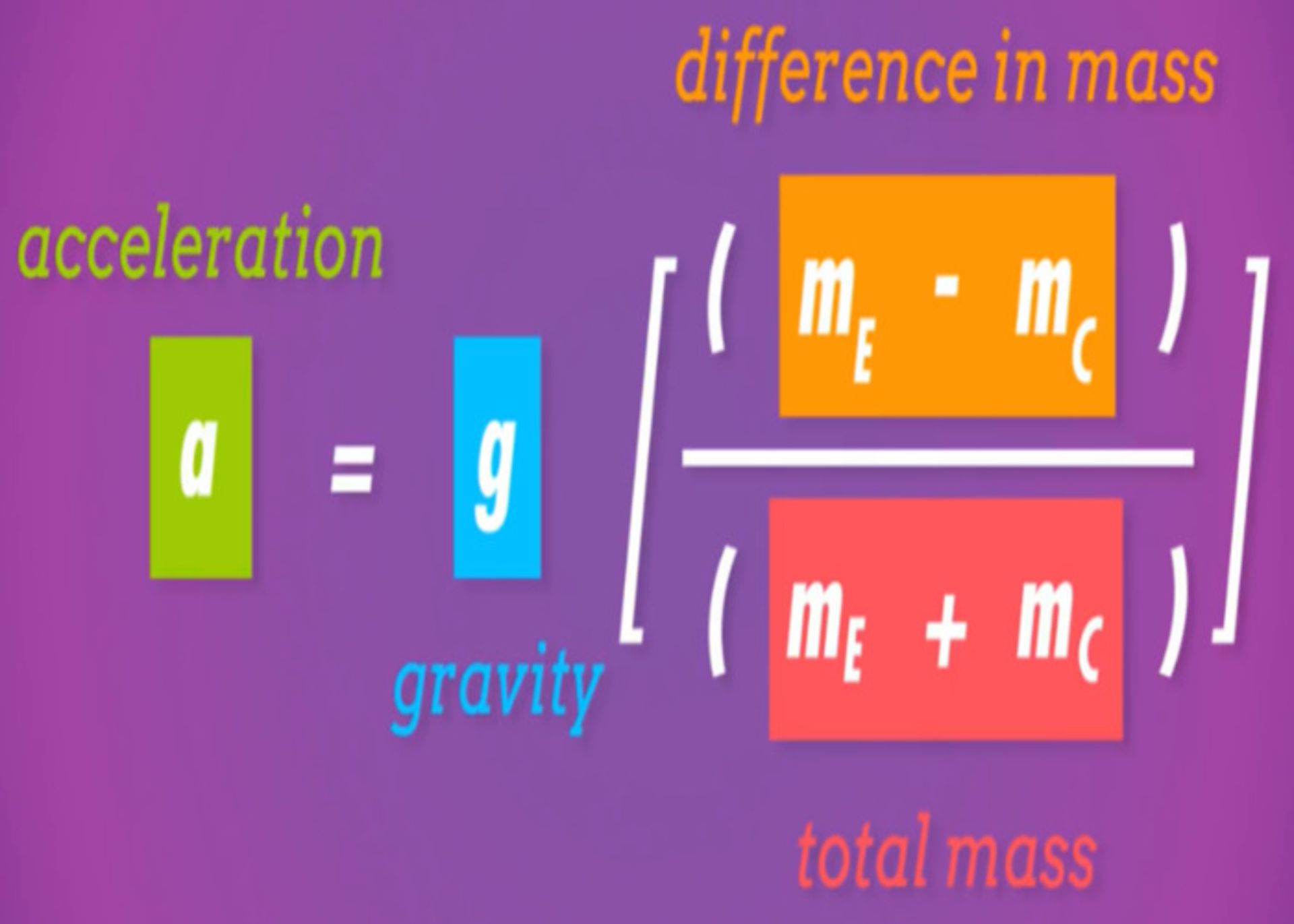
قوانین نیوتون، به همین سادگی جهان کلاسیکی را توصیف میکنند. تاید بر قابل توصیفبودن جهان کلاسیکی بهوسیلهی قوانین نیوتون به این دلیل است که جهان کوانتومی، قوانین دیگری دارد.