۱۰ عدد شگفت‌‌انگیز دنیای ریاضیات

اگر از شیفتگان دنیای ریاضیات هستید، پس احتمالا روز ۱۴ مارس (برابر‌‌با ۲۳ اسفند) به‌‌گوشتان آشناست. این روز، به‌‌عنوان روز جهانی شگفت‌‌انگیزترین و غیرمعقول‌‌ترین عدد دنیا یعنی عدد پی (π) شناخته می‌‌شود. اما این عدد چیست؟ پی را به‌‌سادگی می‌‌توان نسبت محیط یک دایره به قطر آن دانست. این عدد را هرگز نمی‌‌توان کاملا به‌‌صورت اعشاری نوشت. شگفت‌‌انگیزتر آنکه پی، یک عدد متعالی یا غیرجبری است؛ بدین‌معنا که هیچ معادله‌ی چندجمله‌ای با ضرایب گویا را نمی‌توان یافت که ریشه‌ی آن عدد پی باشد.

اما این عدد در خیل عظیم اعداد شگفت‌‌انگیز طبیعت یک استثنا نبوده و نیست. برای بسیاری از ریاضیدانان، اعداد جالب‌‌تری وجود دارد که نسبت‌‌به ثابت دایره، از جذابیت بالاتری برخوردار هستند. در اینجا سعی کرده‌‌ایم فهرستی از اعداد شگفت‌‌انگیزی را برایتان نقل کنیم که از نگاه ریاضیدانان دست‌‌کمی از عدد پی ندارند.

تاو (Tau)

فکر می‌‌کنید چه‌‌چیزی می‌‌تواند جذاب‌‌تر از یک عدد پی باشد؟ شاید مسخره‌‌ترین پاسخ این باشد که بگوییم: دو تا عدد پی! ولی این واقعیت دارد. عدد تاو یا دور (Tau)، مقداری معادل‌با دوبرابر مقدار پی است؛ یعنی چیزی در حدود ۶.۲۸.

جان بائز، ریاضیدانی از دانشگاه کالیفرنیا در ریورساید می‌گوید:

استفاده از تاو می‌‌تواند نسبت‌‌به پی، فرمول‌‌ها را برایمان واضح‌‌تر و منطقی‌تر کند. تمرکز بیشتر ما روی عدد π نسبت‌‌به 2π، تنها ناشی از یک اتفاق تاریخی است.

بائز می‌‌گوید درحقیقت، تاو آن عددی است که در مهم‌ترین فرمول‌‌های ما دیده می‌‌شود. پی درواقع ارتباط میان محیط و قطر آن را مشخص می‌‌کند، درحالی‌‌که تاو، بیانگر ارتباط میان محیط دایره و شعاع آن است و نکته اینجا است که بسیاری از ریاضیدانان بر این عقیده‌‌اند که رابطه‌‌ی دوم بسیار مهم‌تر است. عدد تاو به معادلاتی ظاهرا غیرمرتبط ظاهری متقارن می‌‌بخشد؛ معادلاتی نظیر مساحت دایره یا معادلات توصیف‌گر انرژی جنبشی و کشسانی.

اما در سالگرد گرامیداشت عدد پی، قرار نیست عدد تاو به‌‌دست فراموشی سپرده شود. بنابر تصمیم‌گیری انجام‌گرفته ازسوی مؤسسه‌‌ی فناوری ماساچوست، تاو نیز روز مخصوص‌‌به خودش را خواهد داشت: ۲۸ ژوئن.

پایه‌‌ی لگاریتم طبیعی

عدد جالب دیگری که در اینجا قصد معرفی آن را داریم، پایه‌‌ی لگاریتم طبیعی یا به‌‌اختصار عدد e است که ریاضیدانی سوئیسی لئونارد اویلر در قرن ۱۸ میلادی آن را کشف کرد. این عدد شگفت‌آور با مقدار تقریبی ۲.۷۱۸، ممکن است به‌‌اندازه‌‌ی عدد پی شهرت نداشته باشد؛ ولی عدد e نیز مانند رقیب خود، دارای یک روز مخصوص‌‌به‌‌خود است. اهالی علم، روز ۷ فوریه را برای گرامیداشت این عدد عجیب انتخاب کرده‌‌اند.

پایه‌‌ی لگاریتم طبیعی اغلب در معادلات مربوط به لگاریتم‌‌ها، رشد نمایی و اعداد مختلط استفاده می‌شود. کیت دولین، مدیر پروژه‌‌ی ریاضی اوت‌‌ریچ دانشگاه استنفورد در دانشکده تحصیلات تکمیلی بر این باور است که:

[این عدد] تعریف فوق‌العاده‌ای دارد که بنابر آن، تابع نمایی y=e^x در هر نقطه مقداری برابر با شیب خود دارد. به‌‌عبارت دیگر، اگر مقدار یک تابع در یک نقطه برابر با ۷.۵ باشد، میزان شیب (یا مشتق) آن در آن نقطه نیز برابر با ۷.۵ خواهد بود. این عدد نیز درست مانند دیگر رقبای خود کاربرد فراوانی در ریاضیات، فیزیک و مهندسی دارد.

عدد موهومی i

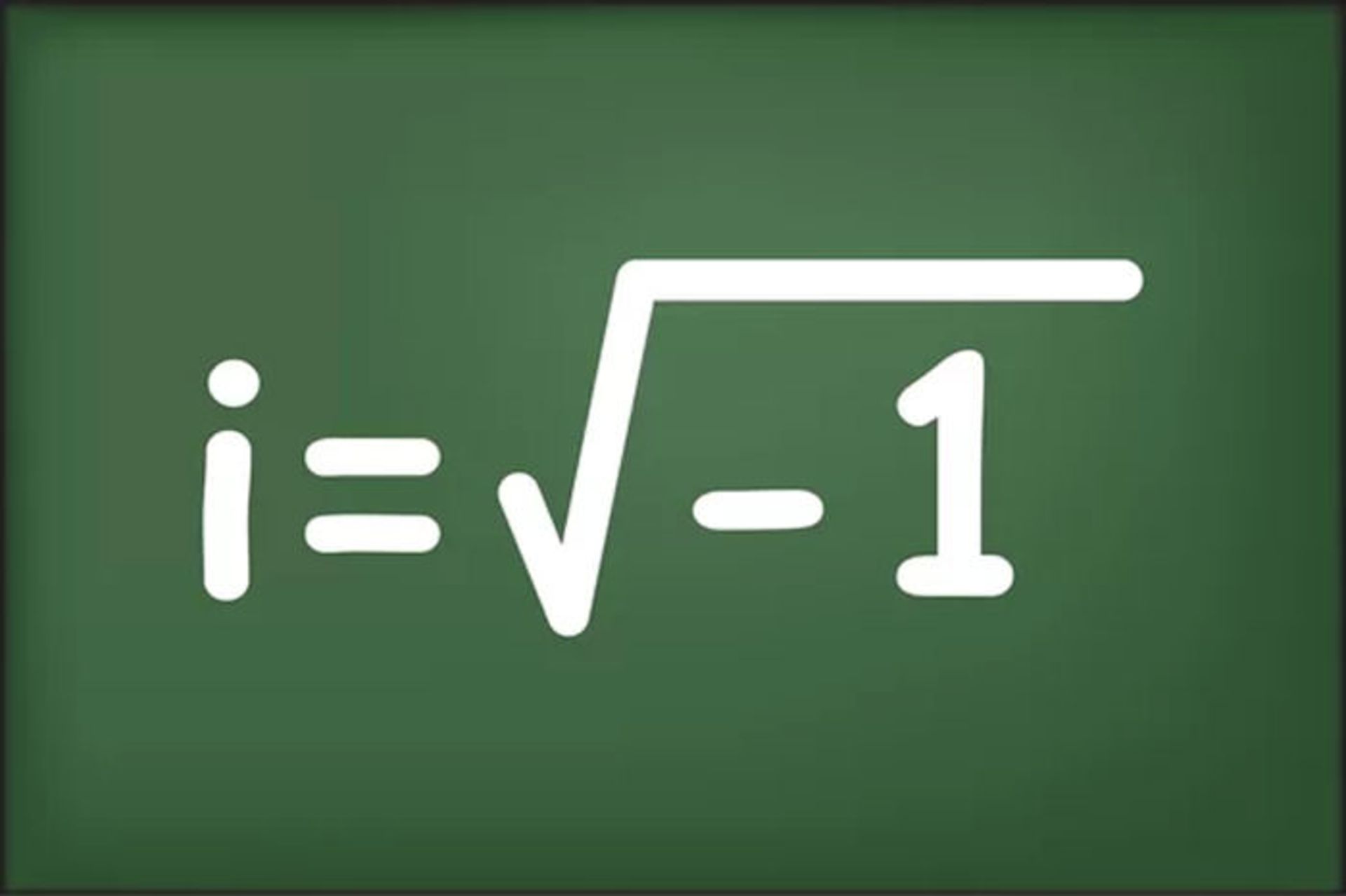
عدد شگفت‌‌انگیزی دیگری نیز وجود دارد که در غرابت کم از عدد پی ندارد: عدد i.

این عدد که جذر ۱- محسوب می‌‌شود، درحقیقت اصلا نباید وجود خارجی داشته باشد؛ چراکه اگر در خلال این سال‌ها، اندک معلوماتی از قوانین پایه‌‌ی ریاضیات در ذهنتان باقی مانده باشد، خوب می‌‌دانید که هرگز نمی‌‌توان از اعداد منفی جذر گرفت.

یوجیبا چنگ، ریاضیدان دانشکده هنر شیکاگو این‌‌گونه می‌‌گوید:

بااین‌حال، اگر ما این قانون را بشکنیم، قادر خواهیم بود اعداد موهومی را اختراع کنیم که همانند اعداد مختلط، اعدادی زیبا و درعین‌حال مفید هستند. دراین‌میان، i یک عدد به‌‌شدت عجیب است؛ چراکه عدد ۱- دارای دو ریشه‌‌ی دوم است: یکی i و دیگری i-. اما درواقع نمی‌‌توان تفاوت میان این دو ریشه را تشخیص داد. از این‌‌رو، ریاضیدانان، تنها یکی از این ریشه‌‌ها را به‌‌عنوان i برگزیدند و دیگری را i-. این بسیار شگفت‌انگیز و خارق‌‌العاده است.

بد نیست بدانید اعداد مختلط، اعدادی هستند که می‌توان آن‌‌ها را به‌‌صورت مجموع دو بخش از عدد حقیقی و عدد موهومی بیان کرد.

i به‌‌توان i

شاید باور کردن آن سخت باشد که وضعیت عدد i می‌‌تواند حتی شگفت‌‌انگیز‌‌تر از آن چیزی باشد که اکنون به نظر می‌‌رسد. برای مثال، شما می‌توانید عدد i را به به‌‌توان خود i برسانید. به عبارت دیگر، ریشه‌‌ی دوم ۱- را به‌توان ریشه‌‌ی دوم ۱- برسانید!

دیوید ریچسون، پروفسور ریاضیات در کالج دیکینسون در پنسیلوانیا و نویسنده‌‌ی کتاب «افسانه‌‌‌‌های غیرممکن: جست‌وجو برای حل مسائل ریاضی دوران باستان» (انتشارات دانشگاه پرینستون) می‌‌گوید:

در نگاه اول، این عدد ممکن است موهومی‌‌ترین عدد ممکن به‌‌نظر برسد؛ عددی موهومی که خود به‌‌توان عددی موهومی رسیده است. اما درحقیقت، همان‌‌طور که لئونارد اویلر طی مقاله‌‌ای در سال ۱۷۴۶ نوشته است: « این یک عدد حقیقی است!»

این محاسبات کمی گیج‌‌کننده به‌‌نظر می‌‌رسد؛ بااین‌حال نتیجه‌‌ی این معادله (در زاویه‌‌ی ۹۰ درجه) نهایتا برابر خواهد بود با ۰.۲۰۷ که عددی کاملا حقیقی است. اگر حوصله‌‌ی سروکله‌‌زدن با نحوه‌‌ی این محاسبات را دارید، می‌‌توانید به این آدرس سری بزنید. ریچسون می‌‌گوید:

همان‌‌طور که اویلر اشاره کرده، i به‌‌توان i دارای یک مقدار واحد نیست. بااین‌حال، رسیدن به این تعداد بی‌‌نهایت از پاسخ‌‌های ممکن، بستگی به آن دارد که معادله را در چه زاویه‌‌ای حل می‌‌کنید.

با این حجم پیچیدگی، بی‌‌دلیل نیست که نمی‌‌توان به اختصاص یک روز خاص برای «i به‌‌توان i» در آینده چندان امید بست.

عدد اول بلفیجور

عدد اول بلفیجور، عدد اولی واروخوانه است که به‌‌صورت ۶۶۶ در میان ۱۳ عدد صفر و یک عدد یک در طرفین نوشته می‌شود (اعداد واروخوانه یا جناس قبل، به اعدادی اطلاق می‌‌شود که خواندن آن از دوطرف یکسان باشد). این عدد نحس (یا به‌تعبیری شیطانی) را می‌توان به شکل ۱۰۰۰۰۰۰۰۰۰۰۰۰۰۶۶۶۰۰۰۰۰۰۰۰۰۰۰۰۰۱ نوشت.

کلیف پیکاور، دانشمند و نویسنده‌‌ای بود که این عدد شیطانی را بانام بلفیجور (یکی از دیوهای هفت‌‌گانه‌‌ی دوزخ) نام‌‌گذاری کرد و شهرت فراوانی به آن بخشید.

این عدد ظاهرا نماد شیطانی مختص‌‌به خودش را دارد که شبیه نماد وارونه‌‌ی عدد پی است. مطابق با اطلاعات درج‌شده در وب‌‌سایت Pickover، این نماد از یک نشان دیده‌‌شده در دست‌نوشته‌‌ی مرموز ووینیچ اقتباس شده است. این دست‌‌نوشته‌‌ی مشهور مجموعه‌ای از تصاویر و متون عجیب است که گویی کسی از آن سر در نمی‌‌آورد.

2aleph_0

دبلیو. هوگ وودین، ریاضیدانی از دانشگاه هاروارد سال‌‌هایی طولانی از وقت خود را صرف تحقیق درمورد اعداد بی‌‌نهایت اختصاص داده است و بنابراین جای تعجبی هم نداشت که یکی از همین اعداد بی‌‌نهایت را به‌‌عنوان عدد دلخواه‌‌ی خود انتخاب کند: 2aleph_0 یا ۲ به‌‌توان aleph-naught.

اعداد آلِف معمولا برای توصیف اندازه‌‌ی مجموعه‌‌های نامحدود مورد استفاده قرار می‌‌گیرند (مجموعه، به هر دسته‌‌ از اشیای متمایز در ریاضیات اطلاق می‌‌شود). یه این ترتیب، مثلا اعداد ۲، ۴ و ۶ می‌توانند باهم یک مجموعه با اندازه‌‌ی ۳ را تشکیل دهند. در مورد اینکه چرا وودین این عدد را انتخاب کرده، خود او می‌‌گوید:

اگر بتوانیم درک کنیم که  2aleph_0 برابر با خود aleph_0 نیست (قضیه‌‌ی کانتور)، آن‌‌گاه خواهیم دانست که اندازه‌‌های متفاوتی از بی‌‌نهایت وجود دارند. این همان مفهومی است که عبارت 2aleph_0  را برایمان خاص می‌‌سازد.

به‌‌عبارت دیگر، همیشه عددی بزرگتر از آنچه می‌‌پنداریم، وجود خواهد داشت. تعدادی نامحدود از اعداد اصلی بی‌‌نهایت وجود دارند و بنابراین هرگز نمی‌‌توان مفهومی را به‌‌عنوان «بزرگ‌ترین عدد اصلی»  تعریف کرد.

ثابت آپری

الیور نیل ریاضیدانی از هاروارد می‌‌گوید:

اگر بخواهم عددی را به‌‌عنوان عدد مورد علاقه‌‌ی خود انتخاب کنم،  این عدد مسلما، ثابت آپری یا (Zeta(3 می‌‌بود؛ چراکه هنوز رازورمزهای بسیاری درمورد آن وجود دارد.

در سال ۱۹۷۹، ریاضیدانی فرانسوی بانام راجر آپری، ثابت کرد که مقداری که بعدها به‌‌عنوان ثابت آپری شناخته شد، عددی گنگ است. این عدد با ۱.۲۰۲۰۵۶۹ آغاز می‌‌شود و اعشار آن تا بی‌‌نهایت ادامه پیدا می‌‌کند. این ثابت همچنین به‌صورت مقدار تابع (Zeta(3 نیز شناخته می‌‌شود که در آن عدد ۳ به‌‌عنوان ورودی تابع زتا (تابعی کشف‌‌شده از سوی ریمن) تعیین شده است.

یکی از بزرگ‌ترین مسائل دنیای ریاضی، فرضیه‌‌ی ریمن است که به پیش‌بینی شرایطی می‌‌پردازد که در آن، تابع زتای ریمن برابر با صفر می‌‌شود؛ فرضیه‌‌ای که اگر درست از آب درآید، این امکان را به ریاضیدانان خواهد داد تا دریابند اعداد اول چگونه توزیع شده‌‌اند. دیوید هیلبرت، ریاضیدان معروف قرن بیستم درمورد فرضیه‌‌ی ریمن می‌‌گوید:

 اگر بعد از هزار سال هم از خواب بیدار می‌‌شدم، باز هم اولین پرسش من این بود که: «آیا فرضیه ریمان ثابت شده‌ است؟»

حال چه‌‌چیزی ثابت آپری را تااین‌‌حد برابمان جذاب کرده است؟ امروزه روشن شده است که ثابت آپری جایگاه ویژه‌‌ای در علم فیزیک دارد، به‌‌خصوص نقش آن در معادلات حاکم بر نیروی مغناطیسی الکترون‌‌ و جهت تکانه‌‌ی زاویه‌ای آن.

عدد یک

اد لتزر، ریاضیدانی از دانشگاه تمپل در فیلادلفیا درمورد شگفت‌‌انگیزترین عدد شناخته‌‌شده، پاسخی تجربی ارائه کرده است:

من فکر می‌کنم این، پاسخی کسالت‌‌بار است؛ اما من باید عدد یک را به‌‌عنوان عدد دلخواه‌‌ خود برگزینم؛ چراکه ازسویی هم یک عدد است و ازسوی دیگر، درباره‌‌ی بسیاری از زمینه‌های انتزاعی، نقش‌‌های متفاوتی ایفا می‌‌کند.

یک تنها عددی است که تمامی اعداد دیگر بدان بخش‌پذیر هستند. همچنین یک تنها عددی است که تنها بر یک عدد مثبت (یعنی خودش) بخش‌‌پذیر است و یک تنها عددی است که نه عددی اول محسوب می‌‌شود و نه مرکب.

در ریاضیات و مهندسی، اغلب اعداد به‌‌صورت مقادیر میان صفر و یک بیان می‌‌شوند. عبارت «صددرصد» تنها یک عبارت فانتزی برای گفتن عدد یک است. یک، عددی جامع و کامل است.

و البته در تمامی علوم بشری، یک به‌‌عنوان واحدی بنیادین شناخته می‌‌شود. مثلا گفته می‌‌شود یک پروتون تنها باری به‌‌اندازه‌‌ی ۱+ دارد. در منطق دودویی، یک به‌‌معنای «بله» است و همچنین یک به‌‌عنوان عدد اتمی سبک‌ترین عنصر دنیا شناخته شده است و نهایتا یک به‌‌عنوان ابعاد یک خط مستقیم نیز تلقی می‌‌شود.

اتحاد اویلر

اتحاد اویلر که درواقع یک معادله است، به‌‌معنای واقعی کلمه، جواهری در ریاضیات به‌‌حساب می‌‌آید. حداقل شاید بتوان گفت این نظری است که ریچارد فینمن، فیزیکدان معاصر درمورد این معادله دارد .این معادله همچنین از لحاظ زیبایی با غزلی از شکسپیر قیاس شده است.

در یک کلام می‌‌توان این‌‌گونه گفت که اتحاد اویلر، پل ارتباطی میان مهم‌‌ترین ثابت‌های ریاضی جهان است: عدد پی، لگاریتم طبیعی و عدد موهومی i. دولین می‌گوید:

[این معادله] توانسته سه ثابت مهم را با مفهوم عدد صفر و مفاهیم ریاضیات پایه به یکدیگر پیوند دهد: e^{i*Pi} + 1 = 0