قوانین فیزیک به کمک هوش مصنوعی می‌آیند

امروزه کامپیوترها می‌توانند خودروها را هدایت کنند، قهرمان‌های جهان را در بازی‌های تخته‌ای مانند شطرنج و Go شکست دهند و حتی نثرهای ادبی بنویسند. بخش زیادی از تحولات هوش مصنوعی به نوع مشخصی از شبکه‌های عصبی مصنوعی وابسته‌اند با الهام از لایه‌های نورون در کورتکس بینایی پستانداران طراحی شده است. توانایی شگفت‌انگیز «شبکه‌های عصبی هم‌گشتی» (CNN-ها) در الگوهای یادگیری داده‌های دوبعدی به‌ویژه در عملیات بینایی کامپیوتر از جمله تشخیص کلمات دست‌نوشته و تشخیص اشیاء در تصاویر دیجیتالی، ثابت شده است.

اما پیاده‌سازی معماری قدرتمند یادگیری ماشین در مجموعه‌های داده‌ای بدون درنظرگرفتن هندسه‌ی مسطح نتیجه‌ی خوبی نخواهد داشت. هندسه‌ی مسطح به مدل‌هایی از اشکال نامنظم گفته می‌شود که در انیمیشن‌های کامپیوتری سه‌بعدی یا ابرهای نقطه‌ای کاربرد دارند که توسط خودروهای خودران برای نقشه‌برداری از محیط اطراف ساخته می‌شوند. در سال ۲۰۱۶، روش جدیدی به‌نام یادگیری عمیق هندسی با هدف خارج کردن CNN-ها از حالت مسطح، ظهور کرد.

یکی از دستاوردهای موفقیت‌آمیز روش‌های جدید یادگیری ماشین، شناسایی دقیق تومورها در سی‌دی اسکن از این روش‌ها می‌توان روزی برای بهبود تشخیص‌های پزشکی استفاده کرد.

امروزه، پژوهشگرها موفق به ارائه‌ی چارچوب جدید تئوری برای ساخت شبکه‌های عصبی شده‌اند. این شبکه‌ها می‌توانند روی انواع سطوح هندسی به یادگیری الگو بپردازند. این شبکه‌ها که با عنوان CNN-های پیمانه‌ای هم شناخته می‌شوند، قادر به تشخیص الگوها در آرایه‌‌ پیکسل‌های دوبعدی و اشیای منحنی نامتقارن و کروی هستند. تاکو کوهن، ماری ویلر، برکی کیکاناگلو و مکس ویلینگ از توسعه‌دهندگان شبکه‌های عصبی همگشتی هستند. ویلینگ می‌گوید: «این چارچوب، پاسخی قطعی به مسئله یادگیری عمیق روی سطوح منحنی است.»

عملکرد CNN-های پیمانه‌ای در یادگیری الگو از داده‌های شبیه‌سازی‌شده‌ی جوی به طرز چشمگیری از شبکه‌های عصبی گذشته بهتر است. داده‌های جوی معمولا روی سطوح کروی نگاشته می‌شوند. الگوریتم‌های یادشده همچنین برای بهبود دید پهپادها و وسایل خودکاری که اشیای سه‌بعدی را زیر نظر دارند و برای شناسایی الگو در داده‌های سطوح منحنی نامنظم قلب، مغز و دیگر اعضای بدن، عملکرد سودمندی دارند.

برای مثال، اندازه‌گیری طول زمین فوتبال را براساس یارد در نظر بگیرید، سپس دوباره آن را براساس متر اندازه‌گیری کنید؛ اعداد به شیوه‌ای قابل پیش‌بینی تغییر خواهند کرد. به‌طور مشابه، فرض کنید دو عکاس از دو نقطه‌ی متفاوت عکس می‌گیرند و خروجی‌های متفاوتی را تولید می‌کنند، اما می‌توان دو تصویر را به یکدیگر ربط داد. هم‌وردایی پیمانه‌ای، سازگاری مدل‌های فیزیکی واقعی را صرف‌نظر از پرسپکتیو یا واحدهای اندازه‌گیری آن‌ها تضمین می‌کند. CNN-های پیمانه‌ای هم دقیقا چنین فرآیندی را روی داده‌ها اجرا می‌کنند. کایل گرانمر، فیزیکدان دانشگاه نیویورک، از یادگیری ماشین برای داده‌های فیزیک ذرات استفاده می‌کند. او می‌گوید:

در فیزیک هیچ جهت‌گیری خاصی وجود ندارد و هدف، رسیدن به نتیجه‌ی مشابهی برای شبکه‌های عصبی است؛ و حالا روش مناسبی برای رسیدن به این نتیجه ابداع شده است.

تاکو کوهن، پژوهشگر یادگیری ماشین در کوالکوم و دانشگاه آمستردام، یکی از معماران ارشد شبکه‌های عصبی همگشتی است.

مایکل برونستین، دانشمند کامپیوتر کالج سلطنتی لندن، در سال ۲۰۱۵، اصطلاح «یادگیری عمیق هندسی» را در سال ۲۰۱۵، به‌عنوان مقدمه‌ای برای رهایی از سطح و طراحی شبکه‌های عصبی با قابلیت یادگیری داده‌های غیرسطحی، ابداع کرد. محبوبیت این روش خیلی زود، افزایش یافت.

برونستین و همکاران او می‌دانستند برای فرا رفتن از صفحه‌ی اقلیدسی باید به بازسازی روالی محاسباتی بپردازند و کارایی شبکه‌های عصبی در تشخیص تصویر دوبعدی را افزایش دهد. این روال که «هم‌گشت» نامیده می‌شود، به لایه‌ای از شبکه‌ی عصبی اجازه می‌دهد عملیات ریاضی را روی بخش‌های کوچکی از داده‌های ورودی اجرا کند و سپس نتایج را به لایه‌ی بعدی در شبکه ارسال کند. برونستین می‌گوید:

می‌توان هم‌گشت را به پنجره‌ای کشویی تشبیه کرد.» شبکه‌ی عصبی هم‌گشتی، تعداد زیادی از این پنجره‌ها را روی فیلترهای شبه‌ داده‌ای ورق می‌زند. هر کدام از فیلترها برای کشف نوع مشخصی از الگوهای داده‌ای طراحی شده‌اند. برای مثال در جستجوی تصویر یک گربه، CNN می‌تواند از فیلترهایی استفاده کند که دیگر لایه‌های شبکه را نادیده می‌گیرند و با اجرای همگشت‌های دیگر، مشخصه‌های سطح بالاتری مثل چشم‌ها، دم یا گوش‌های مثلثی گربه را استخراج می‌کنند. شبکه‌ای عصبی که برای تشخیص گربه‌ها آموزش دیده است از نتایج هم‌گشت‌های لایه‌ای برای تخصیص برچسب «گربه» یا «غیرگربه» به تصاویر، استفاده می‌کند. اما روش CNN تنها روی صفحه عمل می‌کند. به‌گفته‌ی ویلینگ: «با خم شدن صفحه، CNN دچار مشکل می‌شود.

اجرای عمل هم‌گشت روی سطحی منحنی که در هندسه با عنوان خم هم شناخت می‌شود، مانند نگه‌داشتن یکی از مربع‌های کاغذ شطرنجی روی جهان و تلاش برای ردیابی دقیق خط ساحل گرینلند است. برای قرار دادن مربع روی گرینلند باید کل کاغذ را روی سطح فرود آورد و با برداشتن مجدد کاغذ، طرح دچار انحراف می‌شود. از طرفی نگه‌داشتن مربع کاغذی به‌صورت مماس با جهان در یک نقطه و سپس ردیابی لبه‌ی گرینلد در حال دیدن کاغذ (روشی که به آن نقشه‌ی مرکاتور هم گفته می‌شود) هم منجر به ایجاد اعوجاج و انحراف خواهد شد. از طرفی می‌توان کاغذ شطرنجی را به‌جای کره‌ی جغرافیایی روی یک نقشه‌ی کاغذی مسطح قرار داد، اما با این کار میزان انحراف‌ها دو برابر خواهد شد. برای مثال کل لبه‌ی بالایی نقشه تنها یک نقطه در جهان را نشان می‌دهد (قطب شمال)؛ و در صورتی که منحنی، مانند جهان کاملا کروی نباشد و مانند بطری سه‌بعدی یا مولکول پروتئین، پیچیده‌تر و بی‌نظم‌تر باشد، اعمال فرایند هم‌گشت روی آن دشوارتر خواهد شد.

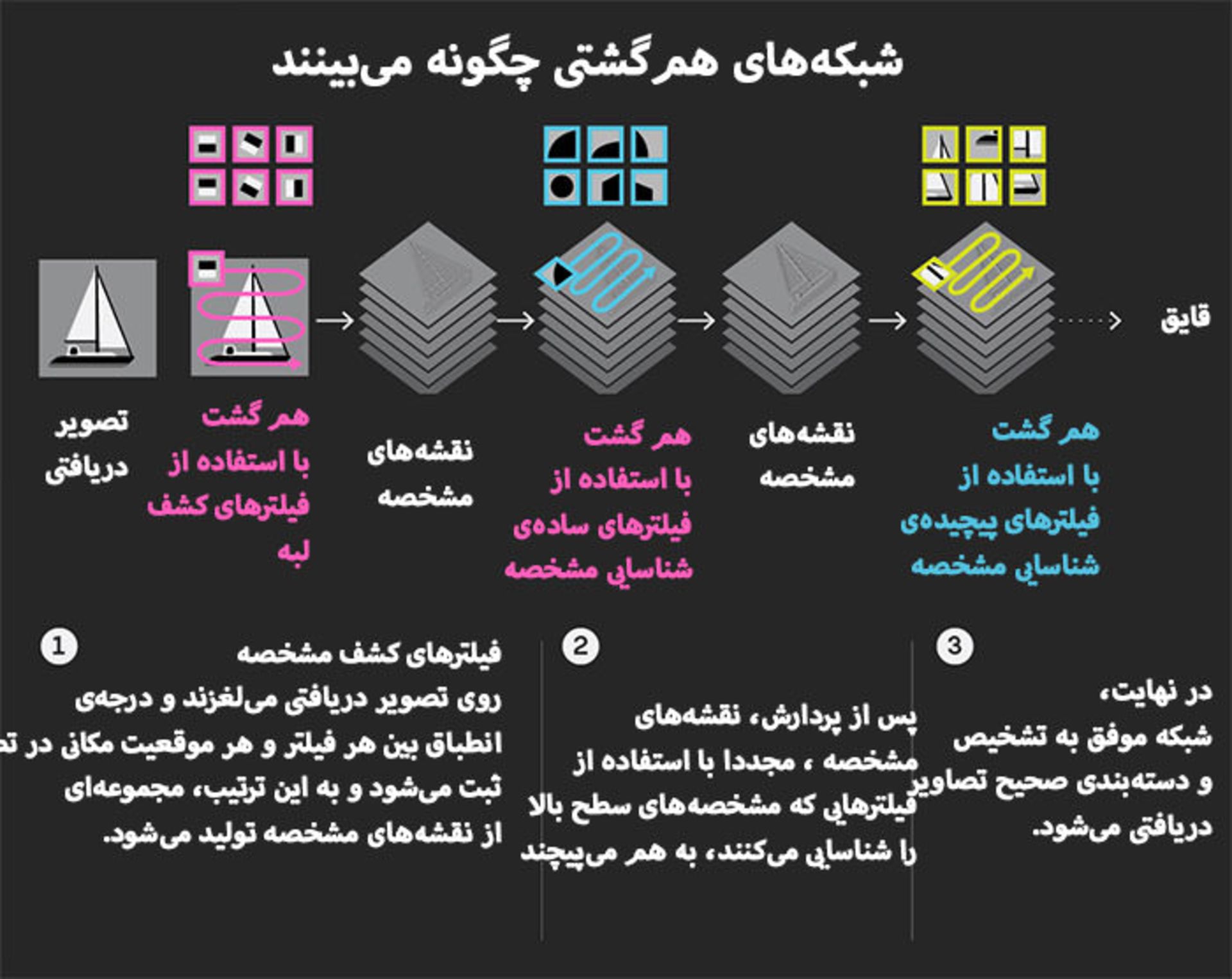
برونستین و همکاران او در سال ۲۰۱۵، راه‌حلی برای مسئله‌ی هم‌گشت روی منحنی‌های غیراقلیدسی ابداع کردند. آن‌ها در این روش، پنجره‌ی کشویی را به‌جای تکه‌ای کاغذ شطرنجی، به تارعنکبوتی مدور تشبیه کردند. به‌طوری‌که بتوان آن‌ را بدون مچاله شدن، کشیدگی یا پارگی روی هر نقطه از سطح منحنی قرار داد.

با تغییر خصوصیات فیلتر کشویی، عملکرد CNN در درک روابط مشخص هندسی، بهبود پیدا کرد. برای مثال در شکلی سه‌بعدی که به دو حالت مختلف خم شده است (مانند فیگور انسانی که ایستاده و انسانی که یک پای خود را بلند کرده است)، الگوریتم تشخیص می‌دهد هر دو حالت، مربوط به یک شیء هستند نه دو شیء متفاوت. تغییرات، بازدهی شبکه‌ی عصبی را در یادگیری به شکل چشمگیری افزایش دادند. به‌گفته‌ی برونستین: «CNN-های استاندارد به مدت چند هفته، از میلیون‌ها نمونه شکل و آموزش استفاده کردند. ما از ۱۰۰ شکل در حالت‌های مختلف برای آموزش در مدت زمان سی دقیقه استفاده کردیم.»

روش‌های یادگیری عمیق، یادگیرنده‌های کم سرعتی هستند. شاید این شبکه‌ها برای تشخیص تصاویر گربه با مشکلات اندکی روبه‌رو شوند اما برای تشخیص سوژه‌های مهم‌تری مانند توده‌های سرطانی در تصاویر بافت ریه یافتن و یافتن داده‌های آموزشی بهینه (که باید از نظر پزشکی دقیق، دارای برچسب و فاقد مشکلات حریم خصوصی باشند) به مشکل برمی‌خورند. هرچقدر تعداد نمونه‌های مورد نیاز برای آموزش به شبکه، کمتر باشد، عملکرد شبکه بهتر خواهد بود.

کوهن می‌دانست یکی از روش‌های مهم برای افزایش کارایی داده‌های شبکه‌های عصبی، استفاده از فرضیه‌های مشخصی درباره‌ی داده‌ها است. برای مثال تومور ریه در صورتی که چرخانده یا منعکس نشود، تفاوتی نخواهد کرد. معمولا، شبکه‌ی هم‌گشتی باید از طریق آموزش، به یادگیری اطلاعات تعداد زیادی از الگوها در جهت‌های مختلف بپردازند. کوهن و ویلینگ در سال ۲۰۱۶، مقاله‌ای را درباره‌ی روش رمزنگاری فرضیه‌ها به‌صورت تقارن‌های هندسی در شبکه‌های عصبی منتشر کردند. این روش تا سال ۲۰۱۸ عملکرد خوبی داشت. درنتیجه کوهن و همکار او، ماریسیا وینکز آن را تعمیم دادند و نتایج امیدبخشی را درباره‌ی تشخیص سرطان ریه در سی تی اسکن‌ها منتشر کردند: شبکه‌ی عصبی آن‌ها تنها با استفاده از یک دهم از داده‌های موردنیاز شبکه‌های دیگر، قادر به شناسایی شواهد بصری بیماری بود. پژوهشگرهای آمستردام به تعمیم روش ادامه دادند و روشی را برای هم‌وردایی پیمانه‌ای ابداع کردند.

شباهت‌های اولیه‌ای بین فیزیک و یادگیری ماشین وجود دارد. به‌گفته‌ی کوهن:

هر دو زمینه با مشاهده و مدلسازی برای پیش‌بینی مشاهدات آینده سروکار دارند. هر دو زمینه به‌دنبال مدل هستند نه اشیای مستقل. برای مثال توصیف اتم‌های هیدروژن متفاوت کافی نیست بلکه باید دسته‌بندی کلی از آن‌ها ارائه داد. فیزیک تاکنون دراین‌زمینه موفق بوده است.

فرضیه‌ی هم وردایی (کواریانس، اصطلاحی که فیزیک‌دان‌ها ترجیح می‌دهند)، از زمان اینشتین رایج شدند و فیزیک‌دان‌ها برای تعمیم مدل‌های خود از آن استفاده کردند. به‌گفته‌ی میراندا چنگ، فیزیکدان نظری دانشگاه آمستردام (یکی از همکاران کوهن در تألیف این مقاله که در حال بررسی ارتباط بین فیزیک و CNN-های پیمانه‌ای است): «توصیف صحیح فیزیک به‌معنی استقلال آن از نوع قوانین و نوع ناظران است». یا به‌گفته‌ی اینشتین در سال ۱۹۱۶: «قوانین طبیعت براساس معادله‌هایی توصیف می‌شوند که در تمام سیستم‌های مختصاتی صدق می‌کنند.»

میراندا چنگ، فیزیک‌دان دانشگاه آمستردام

شبکه‌های هم‌گشتی یکی از موفق‌ترین روش‌های یادگیری عمیق هستند که از نمونه‌ی ساده‌شده‌ی اصل «هم‌وردایی ترجمه» استفاده می‌کنند. فیلتر پنجره‌ای که قابلیت مشخصی را در تصویر شناسایی می‌کند (برای مثال وجوه عمودی) سپس روی صفحه‌ای از پیکسل‌ها می‌لغزد (ترجمه می‌کند) و به رمزنگاری موقعیت‌های لبه‌های عمودی می‌پردازد؛ در مرحله‌ی بعد «نقشه‌ی مشخصه» را می‌سازد که در آن موقعیت‌های مکانی را مشخص کرده است و سپس آن را به لایه‌ی بعدی شبکه ارسال می‌کند. ساخت نقشه‌های مشخصه به خاطر هم‌وردایی ترجمه امکان‌پذیر است: شبکه‌ی عصبی «فرض می‌کند»، یک مشخصه‌ی مشابه می‌تواند در هر نقطه‌ از صفحه‌ی دو بعدی ظاهر شود و می‌تواند لبه‌ی عمودی را به‌عنوان لبه‌ی عمودی در گوشه‌ی بالای راست یا گوشه‌ی پائین چپ تشخیص دهد. ویلر می‌گوید: «نکته‌ی مربوط به شبکه‌های عصبی هم‌وردا، دریافت تقارن‌های واضح و قرار دادن آن‌ها در معماری شبکه‌ای است. امتحان آن مجانی است.»

ویلر، کوهن و مکس ویلینگ همکار آن‌ها در سال ۲۰۱۸، روش یادشده را برای انواع هم‌وردایی توسعه دادند. CNN-های «هم وردای گروهی»، بدون نیاز به آموزش در نمونه‌هایی مشخص، قادر به کشف مشخصه‌های بازتابی و چرخشی در تصاویر مسطح هستند؛ CNN-های کروی هم می‌توانند نقشه‌های مشخصه را براساس داده‌های موجود روی سطح کره بسازند و آن‌ها را دچار انحراف نکنند.

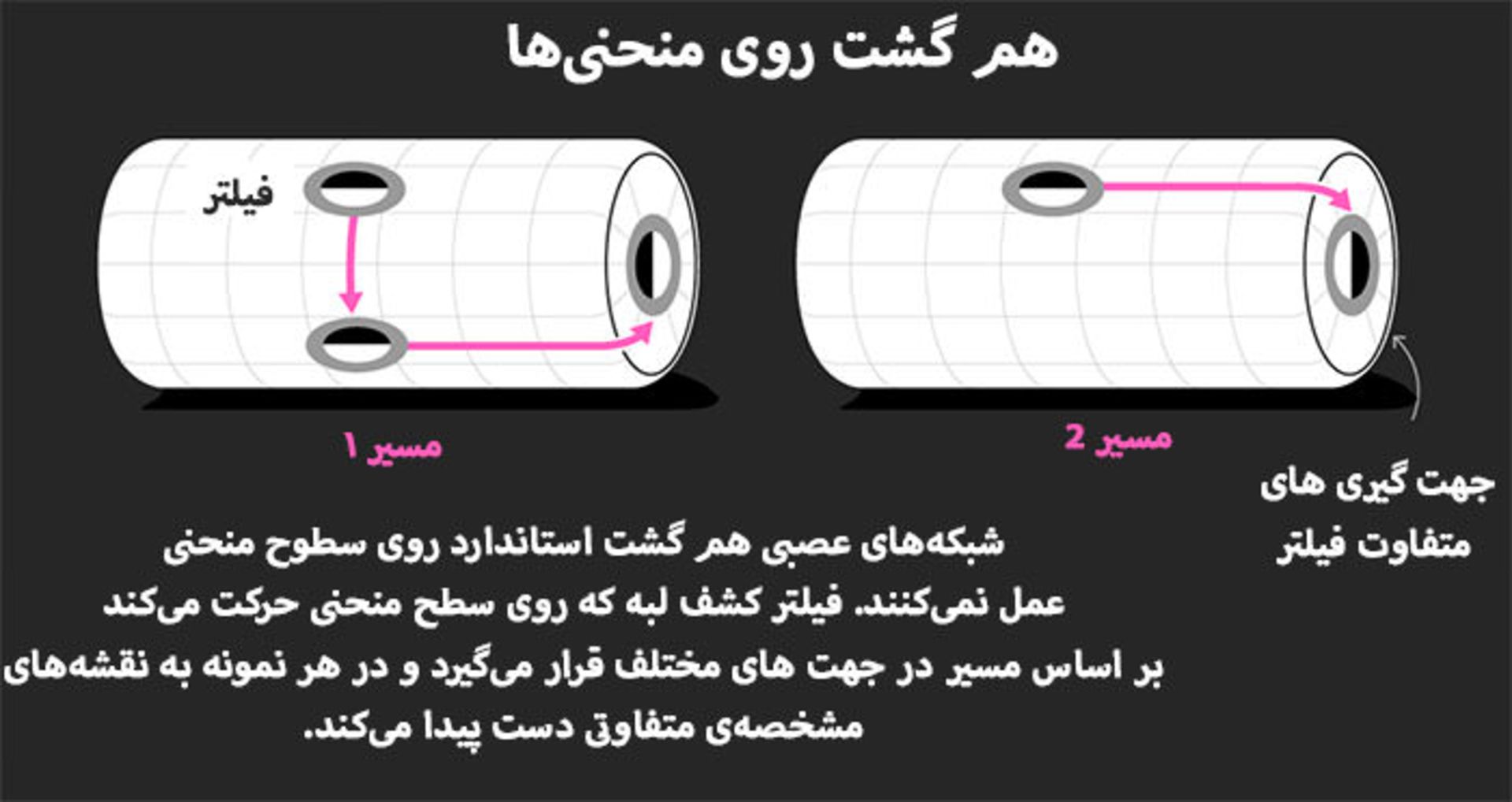
چالش اصلی لغزاندن یک فیلتر مسطح روی سطحی است که بتواند جهت فیلتر را براساس مسیر مشخص دریافتی، تغییر دهد. فرض کنید فیلتر برای کشف یک الگوی ساده طراحی شده است: لکه‌ای سیاه در سمت چپ و لکه‌ای روشن در سمت راست. با لغزش به سمت بالا، پائین، چپ یا راست روی شبکه‌ی مسطح، جهت فیلتر همواره در جهت راست خواهند ماند؛ اما این روند حتی روی سطح کره هم تغییر می‌کند. اگر فیلتر را به اندازه‌ی ۱۸۰ درجه دور استوای کره بچرخانید، جهت فیلتر یکسان باقی می‌ماند: لکه‌ی سیاه در سمت چپ و لکه‌ی روشن در سمت راست. اگر موقعیت خود را به قطب شمال کره تغییر دهید و سپس فیلتر را به همان نقطه منتقل کنید، جهت آن بالا به پائین خواهد شد: لکه‌ی سیاه در سمت راست و لکه‌ی روشن در سمت چپ. درنتیجه فیلتر، همان الگو را کشف نمی‌کند یا همان نقشه‌ی مشخصه را رمزنگاری نمی‌کند. بلکه ممکن است فیلتر با جابه‌جایی در اطراف منحنی‌های پیچیده‌تر، در جهت‌های ناسازگاری قرار بگیرد.

فیزیک‌دان‌ها از زمان اینشتین با مشکل یکسانی سرو کار داشتند و به راه‌حل آن رسیدند: هم‌وردایی پیمانه‌ای. اما به‌گفته‌ی ویلینگ آن‌ها نکته‌ای کلیدی را فراموش کرده‌اند: ردیابی تغییر جهت فیلتر با حرکت در مسیرهای مختلف. آن‌ها فقط می‌توانند جهت یک فیلتر (پیمانه) را انتخاب کنند و سپس روشی سازگار برای تبدیل نقاط آن پیدا کنند.

در روش فوق می‌توان از پیمانه‌های دلخواه در جهت‌گیری اولیه استفاده کرد اما در تبدیل پیمانه‌های دیگر به چارچوب مرجع، باید الگوی اصلی را حفظ کرد. برای مثال، در تبدیل سرعت نور از متر بر ثانیه به مایل بر ساعت، باید کمیت فیزیکی بنیادی را حفظ کرد. به‌گفته‌ی ویلینگ، با روش هم‌وردایی پیمانه‌ای «اعداد واقعی تغییر می‌کنند با این تفاوت که این تغییرات قابل پیش‌بینی خواهند بود.»

کوهن، ویلر و ویلینگ در سال ۲۰۱۹، به رمزنگاری هم‌وردایی پیمانه‌ای به شبکه‌ی عصبی همگشتی پرداختند. آن‌ها محدودیت‌هایی ریاضی را بر داده‌های قابل دیدن برای شبکه‌ی عصبی اعمال کردند؛ لایه‌های شبکه، تنها الگوهای هم‌ارز پیمانه‌ای را نادیده می‌گیرند. به‌گفته‌ی ویلینگ: «می‌توانید هر سطحی شامل سطوح اقلیدسی تا اشیای منحنی دلخواه و منحنی‌های عجیبی مثل بطری کلاین و فضا زمان چهاربعدی را به این الگوریتم بدهید.»

نظریه‌ی CNN-های پیمانه‌ای هم ارز به گونه‌ای تعمیم یافته‌ است که به‌صورت خودکار از فرضیه‌های گذشته‌ی یادگیری هندسی، مثل هم‌وردایی چرخشی و فیلترهای انتقالی روی کره‌ها استفاده می‌کند. حتی روش قبلی مایکل برونستین که امکان تشخیص شکل سه‌بعدی خمیده در حالت‌های مختلف را به شبکه‌های عصبی می‌دهد، در این نظریه صدق می‌کند. برونستین می‌گوید: «هم‌وردایی پیمانه‌ای چارچوب بسیار گسترده‌ای است و تنظیماتی را که در سال ۲۰۱۵ انجام دادیم، شامل می‌شود.»

CNN پیمانه‌ای از دیدگاه تئوری، روی هر سطح منحنی چندبعدی اعمال می‌شود اما کوهن و همکاران او از این روش برای تست داده‌های جوی با ساختار کروی استفاده کردند. آن‌ها از چارچوب هم‌وردای پیمانه‌ای برای ساخت شبکه‌ی عصبی همگشتی استفاده کردند که به منظور کشف الگوهای آب‌وهوایی شدید مثل تندبادهای حاره‌ای در داده‌های شبیه‌سازی جوی، آموزش دیده است. دولت و پژوهشگرهای آکادمیک در سال ۲۰۱۷، از شبکه‌ی هم گشتی استاندارد برای کشف تندبادها با دقت ۷۴ درصد استفاده کردند؛ سال گذشته، CNN پیمانه‌ای موفق به کشف تندبادهایی با دقت ۹۷.۹ درصد شد. (این شبکه نسبت به روش یادگیری عمیق هندسی که در سال ۲۰۱۸ توسعه یافته بود، عملکرد بهتری داشت. روش یادگیری عمیق قبلی، عمومیت کمتری داشت و صرفا مختص سطوح کروی طراحی شده‌ بود. دقت این روش، ۹۴ درصد بود).

مایور مودیگوندا، دانشمند جوی آزمایشگاه ملی برکلی لاورنس، می‌گوید به استفاده از روش‌های یادگیری عمیق به‌ویژه CNN-های پیمانه‌ای ادامه خواهد داد. او می‌گوید: «مشاهده‌ی الگوهای دقیق، صرف‌نظر از جهت‌گیری آن‌ها، جنبه‌ای از هوش بشری انسانی و درست همان‌ چیزی است که به‌دنبال تفسیر آن در انجمن‌های آب‌وهوایی هستیم.» کوالکوم، تولیدکننده‌ی بزرگ تراشه، اخیرا کوهن و ویلینگ را استخدام کرده است و استارتاپ آن‌ها و پروژه‌ی شبکه‌های عصبی آن‌ها را تصاحب کرده است. این شرکت در حال برنامه‌ریزی برای پیاده‌سازی نظریه‌ی CNN-های پیمانه‌ای برای توسعه‌ی کاربردهای بهبودیافته‌ی بینایی کامپیوتر مانند پهپادهایی است که بتوانند به‌صورت آنی، زاویه‌ی دید ۳۶۰ درجه داشته باشند. (اولین نمای فیش آی از دنیا را می‌توان روی یک سطح کروی مانند داده‌ای اقلیمی جهانی نگاشت).

CNN-های پیمانه‌ای توجه بسیاری از فیزیک‌دانها از جمله کرانمر را به خود جلب کرده‌اند. کرانمر قصد دارد از شبکه‌های عصبی برای داده‌های شبیه‌سازی تعامل ذرات زیراتمی استفاده کند. او می‌گوید:

«ما در حال تحلیل داده‌های مربوط به نیروهای هسته‌ای قوی هستیم تا به درکی از درون پروتون برسیم. داده‌ها چهاربعدی هستند؛ بنابراین نمونه‌ی کاربردی بی‌نقصی را برای شبکه‌های عصبی در اختیارمان قرار می‌دهند که دارای هم‌وردایی پیمانه‌ای هستند

ریسی کندور، فیزیک‌دان و پژوهشگر شبکه‌های عصبی هم‌وردا می‌گوید کاربردهای علمی CNN-های پیمانه‌ای ممکن است از کاربرد هوش مصنوعی آن‌ها مهم‌تر باشند. او می‌افزاید: «اگر کار شما تشخیص گربه‌ها در یوتیوب است و نتوانستید گربه‌های وارونه را تشخیص دهید، شاید ضرر زیادی را متحمل نشوید. اما عدم خطای شبکه‌ی عصبی در تشخیص میدان نیرو یا مسیر ذرات برای فیزیک‌دان‌ها اهمیت زیادی دارد؛ زیرا اینجا تنها مسئله‌ی تناسب مطرح نیست. بلکه باید تقارن‌های اصلی را رعایت کرد.»

ریاضی به فیزیک‌دان‌ها در درک بهتر CNN-های پیمانه‌ای و یافتن کاربردهای گسترده‌تری برای آن‌ها کمک می‌کند اما به‌گفته‌ی کوهن، شبکه‌های عصبی هم‌گشتی، نوع جدیدی از فیزیک را معرفی نمی‌کنند. او می‌گوید: «ما حالا قادر به طراحی شبکه‌هایی هستیم که بتوانند انواع داده‌ها را پردازش کنند اما در درجه‌ی اول باید از ساختار داده‌ها آگاه باشید.» به بیان دیگر، فیزیک‌دان‌های می‌توانند از CNN-های پیمانه‌ای استفاده کنند زیرا اینشتین قبلا ثابت کرده است می‌توان از فضازمان به‌عنوان منحنی چهاربعدی استفاده کرد. از طرفی شبکه‌ی عصبی کوهن به خودی خود نمی‌تواند ساختاری را ببیند. بلکه نیاز به یادگیری تقارن‌هایی دارد که انسان در ساخت آن‌ها نقش دارد؛ اما این شبکه‌ها در آینده‌ای نزدیک، کاربردهای گسترده‌تری پیدا خواهند کرد.

کوهن از ایجاد ارتباط بین رشته‌ها لذت می‌برد و حالا موفق شده است این ارتباط را با دقت ریاضی نمایش دهد. او می‌گوید: «من همیشه این درک را داشتم که یادگیری ماشین و فیزیک، عملکرد مشابهی دارند. این ما در آغاز راه این مسئله مهندسی هستیم و با بهبود سیستم‌ها به تدریج می‌توانیم از اتصال‌های متعددی پرده برداریم.»