برنامه‌های کامپیوتری فوق آهسته محدودیت‌های بنیادی ریاضی را آشکار می‌کنند

برنامه‌نویسان معمولا به‌دنبال حداقل‌سازی زمان اجرای کدهای خود هستند؛ اما در سال ۱۹۶۲، تیبور رادو، ریاضی‌دان مجارستانی، مسئله‌ای مخالف را مطرح کرد. او پرسید: «برنامه‌ی ساده‌ی کامپیوتری قبل از توقف چه مدت اجرا می‌شود؟» برخی برنامه‌ها به‌شدت ناکارآمد هستند؛ اما باز‌هم به کارشان ادامه می‌دهند. رادو نام مستعار «سگ‌های آبی مشغول» (Busy Beaver) را به این برنامه‌ها داد.

یافتن برنامه‌های سگ آبی مشغول از سال ۱۹۸۴ به یکی از معماهای گمراه‌کننده برای برنامه‌نویسان و ازجمله سرگرمی‌های ریاضی تبدیل شد. بااین‌حال در سال‌های گذشته، بازی سگ آبی مشغول به موضوع پژوهشی هم تبدیل شده است؛ زیرا با مفاهیم و مسائل بنیادی‌ باز ریاضی در ارتباط بوده است. اسکات آرانسون، دانشمند کامپیوتر تئوری در دانشگاه آستین تگزاس می‌گوید: «در ریاضی، مرز بسیار باریکی بین سرگرمی و مسائل مهم وجود دارد.»

پژوهش جدید نشان می‌دهد جست‌وجوی برنامه‌های کامپیوتری با زمان اجرای طولانی یا برنامه‌های آهسته می‌تواند وضعیت دانش ریاضی را متحول کند و نکات مهمی را آشکار کند. به‌گفته‌ی پژوهشگران، بازی سگ آبی مشغول شاخص منسجمی برای ارزیابی دشواری مسائل مشخص، از‌جمله حدس حل‌نشده‌ی گلدباخ و فرضیه‌ی ریمان است.

به‌طورکلی، بازی سگ آبی مشغول درباره‌ی رفتار ماشین‌های تورینگی است. ماشین‌های تورینگ کامپیوترهای اولیه‌ و ایدئالی هستند که در سال ۱۹۳۶، آلان تورینگ تعریف کرد. ماشین تورینگ عملیات را روی رشته‌ی نوار متناهی انجام می‌دهد که به مربع‌هایی تقسیم شده است. این ماشین عملیات را براساس فهرستی از قوانین اجرا می‌کند. اولین قانون بدین‌ترتیب است:

اگر مربعی شامل عدد ۰ باشد، آن را با عدد ۱ جایگزین کن و مربع را به‌سمت راست منتقل و قانون ۲ را بررسی کن. اگر مربع شامل عدد ۱ باشد، ۱ را رها کن و یک مربع به‌سمت چپ برو و قانون ۳ را بررسی کن.

هر قانون به این سبک است: «ماجراجویی خود را انتخاب کن». برخی قوانین می‌گویند به قوانین قبلی مراجعه کنید و درنهایت، قانونی شامل دستورالعمل «توقف» خواهد بود. تورینگ ثابت کرد این نوع ساده از کامپیوتر براساس دستورالعمل‌های ساده و زمان کافی، می‌تواند محاسبات احتمالی را انجام دهد.

براساس تعریف تورینگ در سال ۱۹۳۶، ماشین تورینگ برای محاسبه‌ی هر چیزی در‌نهایت با دستور «توقف» روبه‌رو می‌شود و در حلقه‌ی بی‌نهایت گرفتار نخواهد شد. باوجوداین، ثابت می‌کند که روش مطمئن و تکراری برای تفکیک ماشین‌هایی که متوقف می‌شوند، از ماشین‌هایی که همیشه اجرا می‌شوند، وجود ندارد.

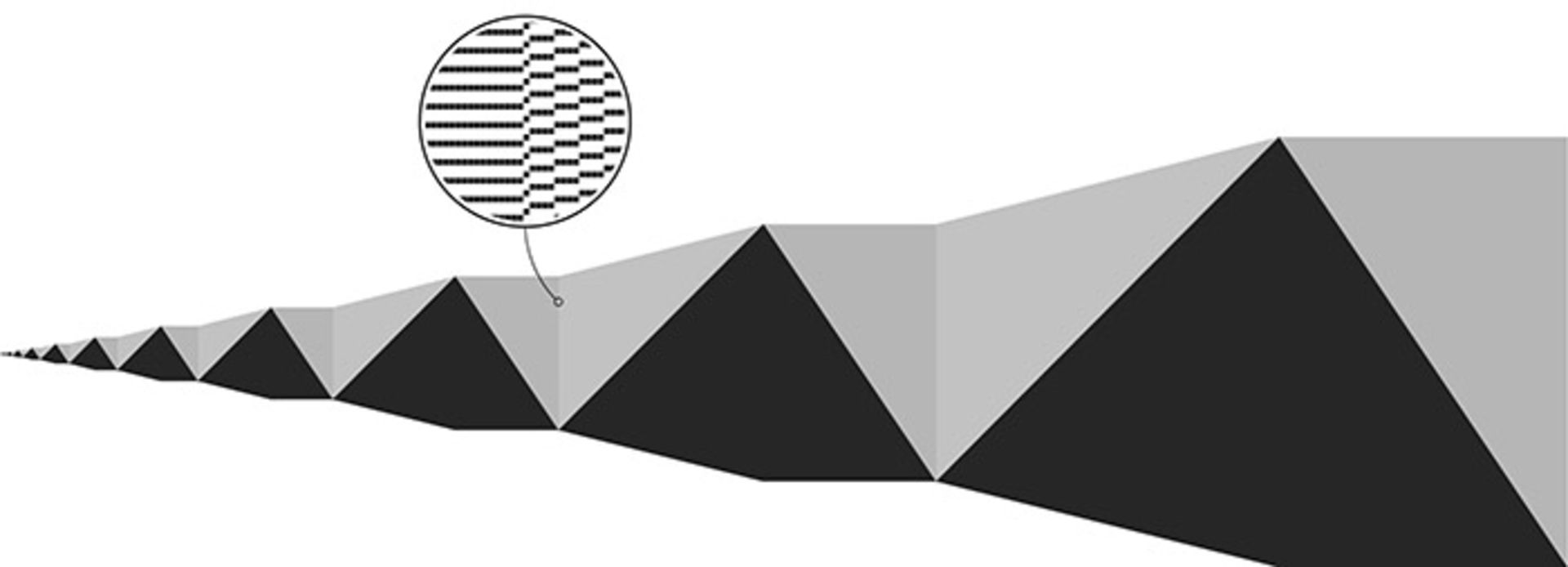
نمایشی بصری از ماشین تورینگ پنج‌قانونی با آهسته‌ترین اجرا. هر ستون از پیکسل‌ها، نشان‌دهنده‌ی یک گام در محاسبات هستند که از چپ به راست حرکت می‌کنند. مربع‌های سیاه هم نشان‌دهنده‌ی موقعیت‌هایی هستند که در آن‌ها ماشین عدد ۱ را چاپ کرده است. ستون سمت راست نشان‌دهنده‌ی وضعیت محاسبات در زمان توقف ماشین تورینگ است.

بازی سگ آبی مشغول این پرسش را مطرح می‌کند: «با‌توجه‌به تعداد مشخصی از قوانین، حداکثر گام‌هایی که ماشین تورینگ می‌تواند قبل از توقف طی کند، چقدر است؟» برای مثال، اگر تنها یک قانون را مجاز کرده باشید و بخواهید از توقف ماشین تورینگ مطمئن شوید، باید بلافاصله دستور توقف را در نظر بگیرید؛ در‌نتیجه، عدد سگ آبی مشغول برای ماشین تک‌قانونی یا (BB(1 برابر با یک است.

با اضافه‌کردن چند قانون بیشتر، تعداد ماشین‌ها هم افزایش می‌یابند. از میان ۶،۵۶۱ ماشین احتمالی دارای دو قانون، ماشینی که در طولانی‌ترین زمان ممکن قبل از عمل توقف اجرا می‌شود (شش مرحله)، سگ آبی مشغول است؛ اما برخی از ماشین‌های دیگر تا ابد ادامه پیدا می‌کنند؛ درنتیجه، هیچ‌کدام از آن‌ها سگ آبی مشغول نیستند. چگونه می‌توان این ماشین‌ها را حذف کرد؟ تورینگ ثابت کرد هیچ روشی وجود ندارد که به‌صورت خودکار نشان دهد ماشینی که برای هزار یا یک‌میلیون گام اجرا می‌شود، در‌نهایت، به‌پایان نخواهد رسید؛ به‌همین‌دلیل، یافتن سگ‌های آبی مشغول کار بسیار دشواری است.

روش کلی برای شناسایی ماشین‌های تورینگ با طولانی‌ترین اجرا و تعداد دلخواه دستورالعمل‌‌ها وجود ندارد. به‌بیان‌بهتر، بازی سگ آبی مشغول محاسبه‌ناپذیر است. اثبات این مسئله که BB(2)=6 و BB(3)=107 به‌اندازه‌ی کافی دشوار بود؛ به‌طوری‌که دانشجوی رادو، شن لین، با انجام این پروژه در سال ۱۹۶۵ موفق شد مدرک دکتری بگیرد. رادو (BB(4 را کاملا ناامیدکننده خواند؛ اما این مسئله در‌نهایت در سال ۱۹۸۳ حل شد.

ویلیام گاسارچ، دانشمند کامپیوتر دانشگاه مریلند و ریاضی‌دانان دیگر به استفاده از بازی به‌عنوان مقیاسی برای اندازه‌گیری دشواری مسائل باز مهم در ریاضیات یا محاسبه‌ی معلوم‌های ریاضی علاقه‌مند هستند. برای مثال، حدس گلدباخ این پرسش را مطرح می‌کند: «آیا هر عدد زوج صحیح بزرگ‌تر از دو جمع دو عدد اول است؟» اثبات این حدس یکی از رویدادهای مهم در نظریه‌ی اعداد است و به ریاضی‌دانان اجازه می‌دهد به درک بهتری از توزیع اعداد اول برسند.

در سال ۲۰۱۵، یکی از کاربران بدون نام گیت‌هاب با نام مستعار Code Golf Addict کدی برای ماشین تورینگ با ۲۷ قانون منتشر کرد. این ماشین متوقف می‌شود، اگر و تنها اگر حدس گلدباخ اشتباه باشد. این ماشین با شمارش صعودی کل اعداد زوج صحیح بزرگ‌تر از چهار کار می‌کند و برای هرکدام، تمام روش‌های احتمالی برای دستیابی به عدد صحیح با جمع دو عدد دیگر را بررسی می‌کند که آیا زوج به‌دست‌آمده اول هستند یا خیر. این ماشین با یافتن زوج مناسب اعداد اول به زوج عدد صحیح بعدی می‌پردازد و فرایند فوق را تکرار می‌کند. اگر یک عدد زوج پیدا کند که حاصل جمع زوج اعداد اول نباشد، متوقف می‌شود.

اجرای ماشین مذکور، روشی کاربردی برای حل حدس گلدباخ نیست؛ زیرا نمی‌توان از توقف آن مطمئن بود؛ اما بازی سگ آبی مشغول تا اندازه‌ای بر این مسئله تأکید می‌کند. اگر امکان محاسبه‌ی BB(27) وجود داشت، سقف انتظاری برای حل خودکار حدس گلدباخ به‌وجود می‌آمد؛ زیرا BB(27) متناظر با حداکثر تعداد مراحلی است که ماشین ۲۷ قانونی تورینگ می‌تواند اجرا کند. اگر تعداد دقیق مراحل را می‌دانستیم، می‌توانستیم ماشین تورینگ را دقیقا براساس همان تعداد تنظیم کنیم. اگر ماشین تورینگ در آن نقطه متوقف شود، بدین‌معنی است که حدس گلدباخ اشتباه است؛ اما اگر مراحل زیادی را اجرا کند، می‌توان با اطمینان گفت حدس صحیح هستند.

البته (BB(744 از‌نظر تعداد قوانین، بسیار بیشتر از (BB(27 است؛ اما کار با نمونه‌ای ساده‌تر مثل (BB(5، می‌تواند به مطرح‌شدن پرسش‌های جدیدی در زمینه‌ی نظریه‌ی اعداد منجر شود که در نوع خود جذاب هستند. برای مثال، ریاضی‌دانی به‌نام پاسکال میشل در سال ۱۹۹۳ ثابت کرد ماشین تورینگ پنج‌قانونی رفتار مشابه با تابع حدس کولاتز دارد که مسئله‌ی باز مشهوری در نظریه‌ی اعداد است. آرانسون می‌گوید:

بخش زیادی از ریاضیات را می‌توان با این پرسش رمزنگاری کرد: آیا این ماشین تورینگ متوقف می‌شود یا خیر؟ اگر تمام اعداد سگ آبی مشغول را بشناسید، به تمام این پرسش‌ها می‌توانید پاسخ دهید.

اخیرا آرانسون از مقیاس سگ آبی مشغول به‌منظور اندازه‌گیری «آستانه‌ی مجهولیت» برای کل سیستم‌های ریاضی استفاده کرد. نظریه‌های ناقص و مشهور گودل از ۱۹۳۱ نشان می‌دهند هر مجموعه‌ای از قواعد اولیه که بتوانند به‌عنوان مبنایی منطقی و احتمالی برای ریاضیات عمل کنند، به یکی از این دو سرنوشت دچار خواهند شد: ۱. قواعد می‌توانند ناسازگار باشند و به تناقض‌هایی مثل ۰=۱ منجر شوند؛ ۲. قواعد می‌توانند ناقص باشند و برخی از قضیه‌های صحیح عددی را نتوانند اثبات کنند (مثلا این حقیقت که ۲+۲=۴ است). سیستم بدیهی شالوده‌ی کل ریاضیات مدرن به‌عنوان نظریه‌ی مجموعه‌ی زرملوفرانکل (ZF) شناخته می‌شود و محدودیت‌های گودلی دارد. حالا آرانسون می‌خواهد از بازی سگ آبی مشغول برای شناسایی موقعیت این سیستم‌ها استفاده کند.

در سال ۲۰۱۶، آرانسون و دانشجوی او، آدام یدیدیا، نوعی ماشینی تورینگ با ۷،۹۱۰ قانون را تعریف کردند. این ماشین فقط زمانی متوقف می‌شود که نظریه‌ی مجموعه‌ی ZF ناسازگار باشد؛ یعنی (BB(7910 محاسبه‌ای است که قواعد نظریه‌ی ZF را نادیده می‌گیرد. با این قواعد، نمی‌توان درستی نتیجه‌ی (BB(7910 را ثابت کرد و برای مثال، نشان داد نتیجه‌ی ۲+۲=۴ است، نه ۵.

اوریر نوعی ماشین ساده‌تر با ۷۴۸ قانون طراحی کرد. این ماشین صرفا زمانی متوقف می‌شود که ZF ناسازگار باشد. به‌طور‌کلی، آستانه‌های مجهولیت این‌چنینی قطعا وجود دارند و به‌گفته‌ی آرانسون، این چشم‌اندازی از جهان است که از زمان گودل وجود داشته و تابع سگ آبی مشغول روشی برای پیاده‌سازی آن‌ها در نمونه‌های واقعی است.