کشف راه‌حلی دقیق برای مسئله ریاضی ساده‌ای پس از قرن‌ها

این مسئله ساده به‌نظر می‌رسد: حصاری مدوّر را در نظر بگیرید که زمین چمن را محصور کرده است. اگر بزی را با طناب به داخل حصار ببندید، چقدر طناب نیاز دارید تا حیوان بتواند دقیقا به نیمی از زمین دسترسی پیدا کند؟ به‌نظر می‌رسد مسئله‌ی مذکور به‌سادگی مسائل دبیرستان باشد؛ اما ریاضی‌دانان و علاقه‌مندان ریاضی بیش از ۲۷۰ سال به‌دنبال راه‌حلی ساده برای این مسئله بودند و با اینکه توانستند راه‌حل‌هایی برایش پیدا کنند، پاسخ‌ها ناقص و مبهم بودند. مارک میرسون، ریاضی‌دان آکادمی نیروی دریایی ایالات متحده‌ی آمریکا، درباره‌ی این موضوع می‌گوید:

حتی پس از ۲۷۰ سال، هنوز کسی پاسخ دقیقی برای مسئله‌ی بز محصور پیدا نکرده است. راه‌‌حل فقط به‌صورت تقریبی ارائه شده است.

در آغاز سال ریاضیدانی آلمانی به نام اینگو اولیسچ در نهایت موفق به پیشرفت در حل این مسئله شد و راه‌حلی دقیق را برای آن پیدا کرد. گرچه این راه‌حل از دیدگاه خواننده چندان مناسب و مستقیم نبود. بااین‌حال به گفته‌ی مایکل هریسون، ریاضیدن دانشگاه کارنیگ ملون:

پاسخ اولیسچ اولین پاسخ دقیق برای طول طناب است و پیشرفت مهمی به شمار می‌رود.

البته دستیابی به پاسخ دقیق برای مسئله‌ی بز محصور متون ریاضی یا پژوهش‌ها را متحول نخواهد کرد؛ زیرا به‌عقیده‌ی اولیسچ این مسئله، مسئله‌ای منزوی است و ربط زیادی به مسائل دیگر ندارد و در نظریه‌ی ریاضیات تعبیه نشده است؛ اما مسائل سرگرم‌کننده‌ی این‌چنینی می‌توانند ایده‌های جدید ریاضی را ارائه کنند و به پژوهشگران در یافتن راه‌حل‌های جدید برای مسائل دیگر کمک کنند.

اولین مسئله‌‌ی مشابه بز محصور در سال ۱۷۴۸ در مجله‌ی The Ladies Diary منتشر شد. در سناریو اصلی مسئله، اسبی برای غذاخوردن در پارک جنتلمن محصور شده است. در این نمونه، اسب خارج از حصار قرار دارد. اگر طول طناب به‌اندازه‌ی محیط حصار باشد، حداکثر مساحت تغذیه‌ی اسب چقدر است؟ این نسخه در گروه مسئله‌ی «خارجی» دسته‌بندی شده است؛ زیرا اسب خارج از حصار دایره‌ای قرار دارد. پاسخ به مسئله‌ی یادشده در نسخه‌ی ۱۷۴۹ مجله‌ی Diary منتشر شد. این مسئله را شخصی به‌نام آقای هیت با استفاده از جدول لگاریتمی حل کرد. پاسخ هیت ۷۶۲۵۷.۸۶ یارد مربع برای طناب ۱۶۰ یاردی بود که تقریبا راه‌حلی دقیق به‌شمار می‌رفت.

در سال ۱۸۹۴، مسئله دوباره در اولین نسخه‌ از ماهنامه‌ی ریاضی آمریکایی با عنوان مسئله‌ی چرنده‌ای در حصار مطرح شد؛ ولی این بار بدون اشاره‌ به حیوانات مزرعه. این نوع مسئله در دسته‌ی فضای داخلی قرار می‌گیرد و دشوارتر از مسئله‌ی خارج از حصار است. در مسئله‌ی خارج از حصار، حل مسئله با شعاع دایره و طول طناب آغاز و مساحت محاسبه می‌شود. همچنین، می‌توان ازطریق انتگرال مسئله را حل کرد.

در سال‌های بعد، ماهنامه‌ی ریاضی انواع مختلفی از مسئله‌ی فضای داخلی را منتشر کرد که به‌جای بز، از اسب نام برده بود و حصارها هم به شکل‌های دایره و مربع و بیضی بودند؛ اما در دهه‌ی ۱۹۶۰، به‌دلایل نامعلومی بزها جای اسب‌های را در مسئله‌ی چرنده در حصار گرفتند. این در حالی است ‌که به‌گفته‌ی مارشال فریسرِ ریاضی‌دان، بزها معمولا کمتر تابع افسار هستند.

در سال ۱۹۸۴، فریزر مسئله را از حالت مسطح خارج کرد و آن را به ابعاد بزرگ‌تر تعمیم داد. او مسئله را به این صورت تغییر داد: چقدر طناب لازم است تا بز بتواند دقیقا نیمی از حجم کره‌ی n بعدی بچرد؟ در این مسئله، n به‌سمت بی‌نهایت میل می‌کند. میرسون خطایی منطقی را در این مسئله کشف کرد و همان سال اشتباه فریزر را تصحیح کرد؛ اما به یک نتیجه رسید: با میل n به مست بی‌نهایت، نسبت طناب افسار به شعاع کره به رادیکال دو می‌رسد.

به‌گفته‌ی میرسون، روش به‌ظاهر پیچیده‌ی یادشده برای حل مسئله‌ در فضای چند‌بُعدی، یافتن راه‌حل را آسان‌تر می‌سازد. او می‌افزاید:

در ابعاد بی‌نهایت به پاسخ شفافی می‌رسیم؛ درحالی‌که در دو بُعد چنین پاسخ واضحی وجود ندارد.

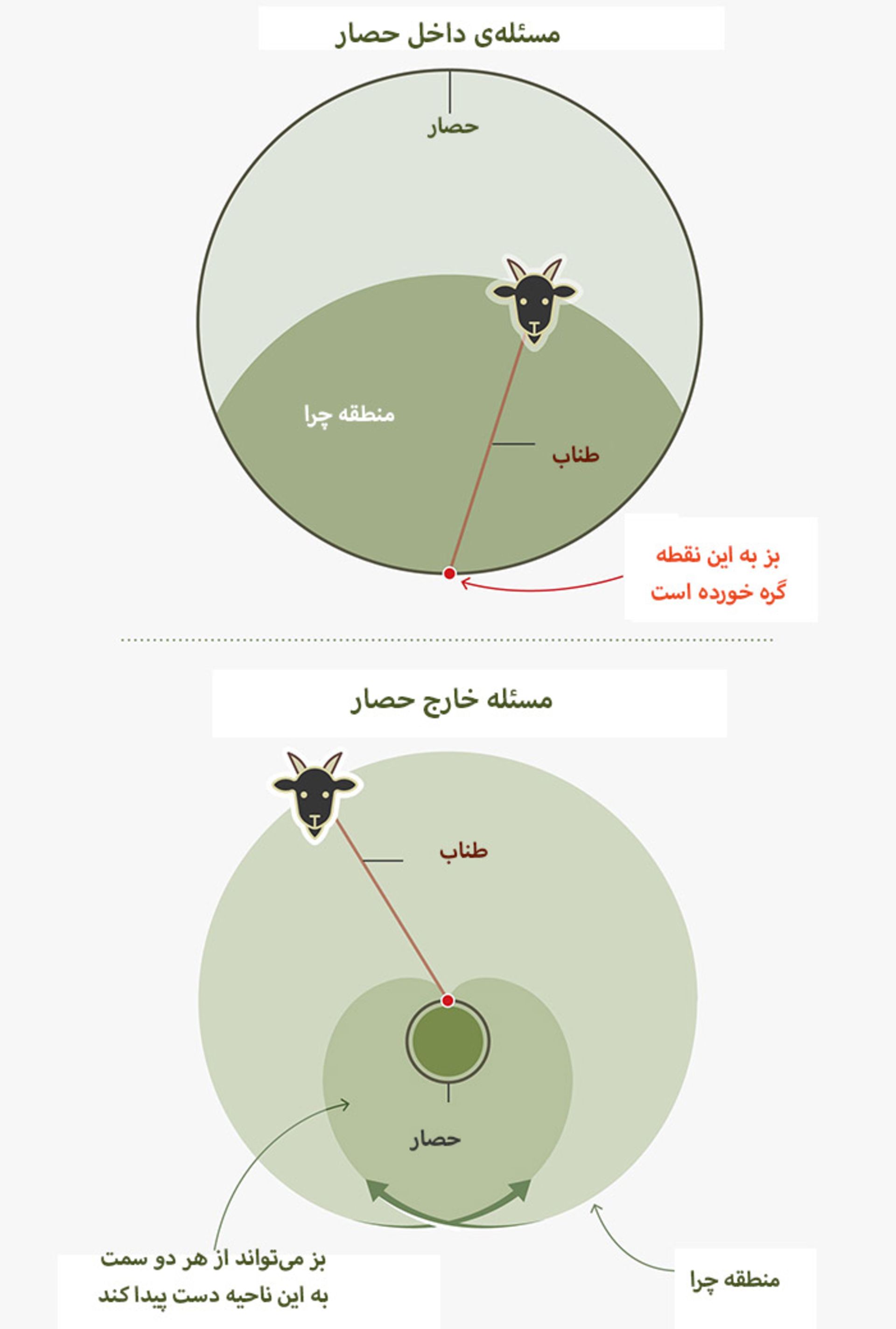
مسئله‌ی بز محصور به دو شکل مطرح می‌شود؛ اما همیشه با بزی آغاز می‌شود که به حصاری مدوّر بسته شده است. نسخه‌ی داخلی بدین‌صورت مطرح می‌شود: اگر بز بخواهد دقیقا به نیمی از ناحیه‌ی محصور دسترسی پیدا کند، چقدر طناب لازم است؟ نسخه‌ی خارجی بدین‌ترتیب مطرح می‌شود: با وجود طول مشخص طناب و محیط حصار، بز به چقدر از مساحت خارجی دسترسی پیدا خواهد کرد؟ گفتنی است در این نمونه، طول طناب برابر با محیط حصار است.

مایکل هافمن، از ریاضی‌دانان آکادمی نیروی دریایی ایالات متحده‌ی آمریکا، در سال ۱۹۹۸ مسئله را به‌ گونه‌ای دیگر توسعه داد. هدف این مسئله اندازه‌گیری مساحت موجود برای گاوی است که به خارج از سیلوی دایره‌ای بسته شده است. هافمن تصمیم گرفت فضای خارجی را نه‌تنها برای دایره، بلکه برای هر منحنی مسطح دیگری از‌جمله بیضی و حتی منحنی‌های غیر‌بسته توسعه دهد.

اخیرا گراهام جیمسون، ریاضی‌دان دانشگاه لنکستر، نمونه‌ی سه‌بُعدی مسئله‌ی داخل حصار را همراه‌با پسرش، نیکولاس، حل کرده است. ازآنجاکه بزها نمی‌توانند به‌راحتی در سه بُعد حرکت کنند، جیمسون در مقاله‌ی سال ۲۰۱۷ این مسئله را «مسئله‌ی پرنده» نامید: اگر پرنده‌ای را داخل قفل کروی ببندید، چقدر افسار یا بند لازم است تا پرنده بتواند به نیمی از حجم قفس دسترسی پیدا کند؟

با وجود تمام تغییرات، راه‌حل دقیق مسئله‌ی دوبُعدی داخلی حصار از سال ۱۸۹۴ مبهم باقی مانده بود تا اینکه اولیسچ در سال جاری راه‌حلش را ارائه کرد. او کار روی این مسئله را در سال ۲۰۱۷ و پس از دریافت مدرک دکتری از دانشگاه مانستر آغاز کرد. اولیسچ به‌دنبال توسعه‌ی روشی جدید برای حل مسئله بود.

مسئله‌ی بز را می‌توان به معادله‌ای غیرجبری تبدیل کرد که براساس تعریف، توابع مثلثاتی مثل سینوس و کسینوس را شامل می‌شود؛ اما هدف اولیسچ تبدیل مسئله به معادله‌ای رام‌شدنی بود. او متوجه شد با استفاده از تحلیل پیچیده می‌تواند به چنین راه‌حلی دست پیدا کند. تحلیل پیچیده شاخه‌ای از ریاضیات است که از ابزار تحلیلی مانند حسابان برای توصیف اعداد پیچیده استفاده می‌کند. ریاضی‌دانان قرن‌هاست که از تحلیل پیچیده استفاده می‌کنند؛ ولی اولیسچ اولین‌بار از این روش برای حل مسئله‌ی بز گرسنه استفاده کرده است.

در ریاضیات یافتن روش‌های جدید برای رسیدن به پاسخ ارزشمند است؛ حتی اگر مسئله قبلا حل شده باشد؛ زیرا می‌توان مسئله را به روش‌های مختلفی تعمیم داد.

هافمن قدری خوش‌بین‌تر است. معادله‌ی غیرجبری اولیسچ به معادلات غیرجبری هافمن در مقاله‌ی سال ۲۰۱۷ ربط دارند و هافمن با بررسی مقاله‌‌ی سال ۱۹۵۳ به این معادلات علاقه‌مند شد. او راه‌‌حل‌های موازی را‌ برای حل مسئله در نظر دارد و می‌گوید:

تمام پیشرفت‌های علم ریاضی از کشف‌های بنیادی سرچشمه نمی‌گیرند. گاهی با بررسی روش‌های کلاسیک و یافتن زاویه‌ای جدید می‌توان به نتایج جدید دست یافت.

مقاله‌ی اصلی با مجوز Quanta Magazine منتشر شد.