دنباله فیبوناچی؛ الگوی اسرارآمیز طبیعت

 آیا تابه‌حال به وجه اشتراک چهره‌ی خود با تخم مرغ، یا وجه شباهت آفتاب‌پرست با آناناس فکر کرده‌اید؟ جهان هستی جای باشکوه و بی‌نهایت پیچیده‌ای است که در آن می‌توان بین عناصر به‌ظاهر نامربوط، رابطه‌ای پیدا کرد. تکرار بی‌شمار الگوهای مشابه در طبیعت به شکل‌گیری سناریوهای مبهوت‌کننده‌ای انجامیده است که به کمک ریاضی به‌راحتی قابل توضیح هستند. 

به قول آرتور بنجامین، ریاضیدان معروف آمریکایی، افراد اغلب به سه دلیل ریاضی یاد می‌گیرند: برای انجام محاسبات، برای به کار بردن آن در حوزه‌های مختلف و برای الهام گرفتن از آن.

اما چرا نخواهیم ریاضی را فقط به خاطر اینکه زیبا، سرگرم‌کننده یا هیجان‌انگیز است، یاد بگیریم؟ یک مدل ریاضی که هر سه‌ی این ویژگی‌ها را دارد، دنباله‌ی اعداد فیبوناچی (fibonacci) است؛ اما چرا این دنباله این‌قدر معروف است؟ از دید محاسباتی، درک این دنباله بسیار آسان است: ۱ به اضافه‌ی ۱ می‌شود ۲؛ ۲ به اضافه‌ی ۱ می‌شود ۳؛ ۳ به اضافه‌ی ۲ می‌شود ۵ و الی آخر. 

از دید کاربردی هم اعداد فیبوناچی به‌وفور در طبیعت یافت می‌شوند. تعداد گلبرگ‌های گل، شکل تخم‌مرغ و آناناس، پیچش دم آفتاب‌پرست یا چینش مارپیچی تخم‌های گل آفتابگردان از دنباله‌ی فیبوناچی پیروی می‌کنند. 

اما دنباله‌ی اعداد فیبوناچی دقیقا چیست و داستان آن از کجا شروع شد؟ با این مقاله همراه باشید.

دنباله‌ی اعداد فیبوناچی یکی از معروف‌ترین دنباله‌های ریاضی است که احتمالا نام‌ آن را به‌دفعات در جاهای مختلف، از جمله فیلم و سریال، کتاب و موسیقی و حتی دنیای اقتصاد، شنیده باشید. هر عدد در این دنباله از مجموع دو عدد قبلی آن به دست می‌آید؛ یعنی:

 ۰, ۱, ۱, ۲, ۳, ۵, ۸, ۱۳, ۲۱, ۳۴٬ …

معادله‌ی ریاضی مربوط به این دنباله به این صورت است:‌

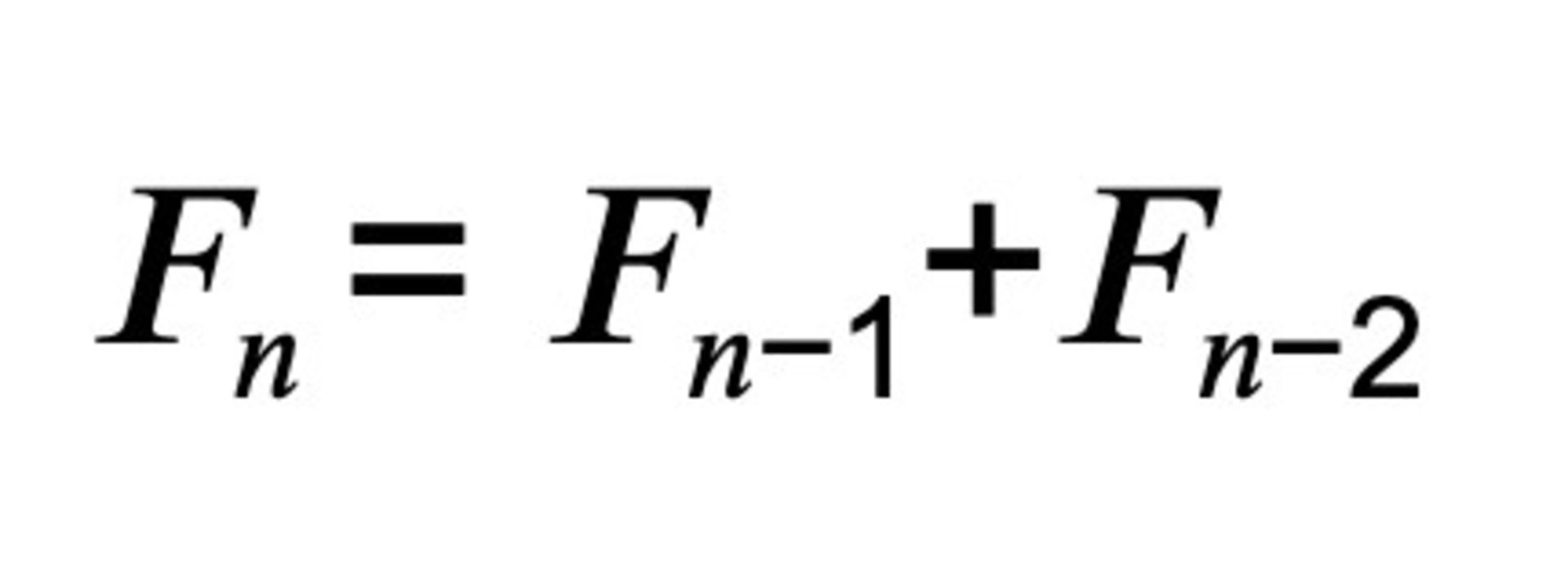
به این دنباله به دلایلی که در ادامه بیشتر با آن‌ها آشنا خواهید شد، «راز مخفی طبیعت» و «قانون جهانی طبیعت» نیز می‌گویند. این دنباله را می‌توان تقریبا در ابعاد هر چیزی که در جهان است، از هرم بزرگ جیزه در مصر گرفته تا صدف‌ها، صورت و اندام انسان و حتی کهکشان‌ها مشاهده کرد؛ و به احتمال زیاد، هر چیزی که تاکنون درباره‌ی این دنباله می‌دانستید، اشتباه است. 

اما داستان واقعی پیدایش این دنباله‌ی مشهور چیست؟ 

اما لئوناردو دنباله‌ی فیبوناچی را کشف نکرد؛ از این دنباله اولین‌بار در متون سانسکریت که از سیستم اعداد هندو-عربی استفاده می‌کردند، نام برده شده بود و این متون قرن‌ها پیش از لئوناردو دا پیزا وجود داشته‌اند.

پس ارتباط لئوناردو دا پیزا با دنباله‌ی فیبوناچی چیست؟ این ریاضیدان در سال ۱۲۰۲، کتاب قطور «Liber Abaci»‌ را برای آموزش محاسبات ریاضی منتشر کرد. این کتاب که برای بازرگانان نوشته شده بود، از محاسبات هندو-عربی برای ردیابی سود، زیان و محاسبه‌ی تراز باقیمانده وام استفاده کرده بود. لئوناردو جایی از کتاب، این دنباله را برای حل مسئله‌ای مربوط به زاد و ولد خرگوش‌ها معرفی کرده بود. مسئله به این صورت است:

فرض کنید یک خرگوش نر و یک خرگوش ماده دارید. بعد از یک ماه، این دو خرگوش صاحب دو خرگوش نر و ماده‌ی دیگر می‌شوند. ماه بعد، این خرگوش‌های جدید هم دو خرگوش نر و ماده‌ی دیگر به دنیا می‌آورند. سال بعد چند جفت خرگوش خواهید داشت؟

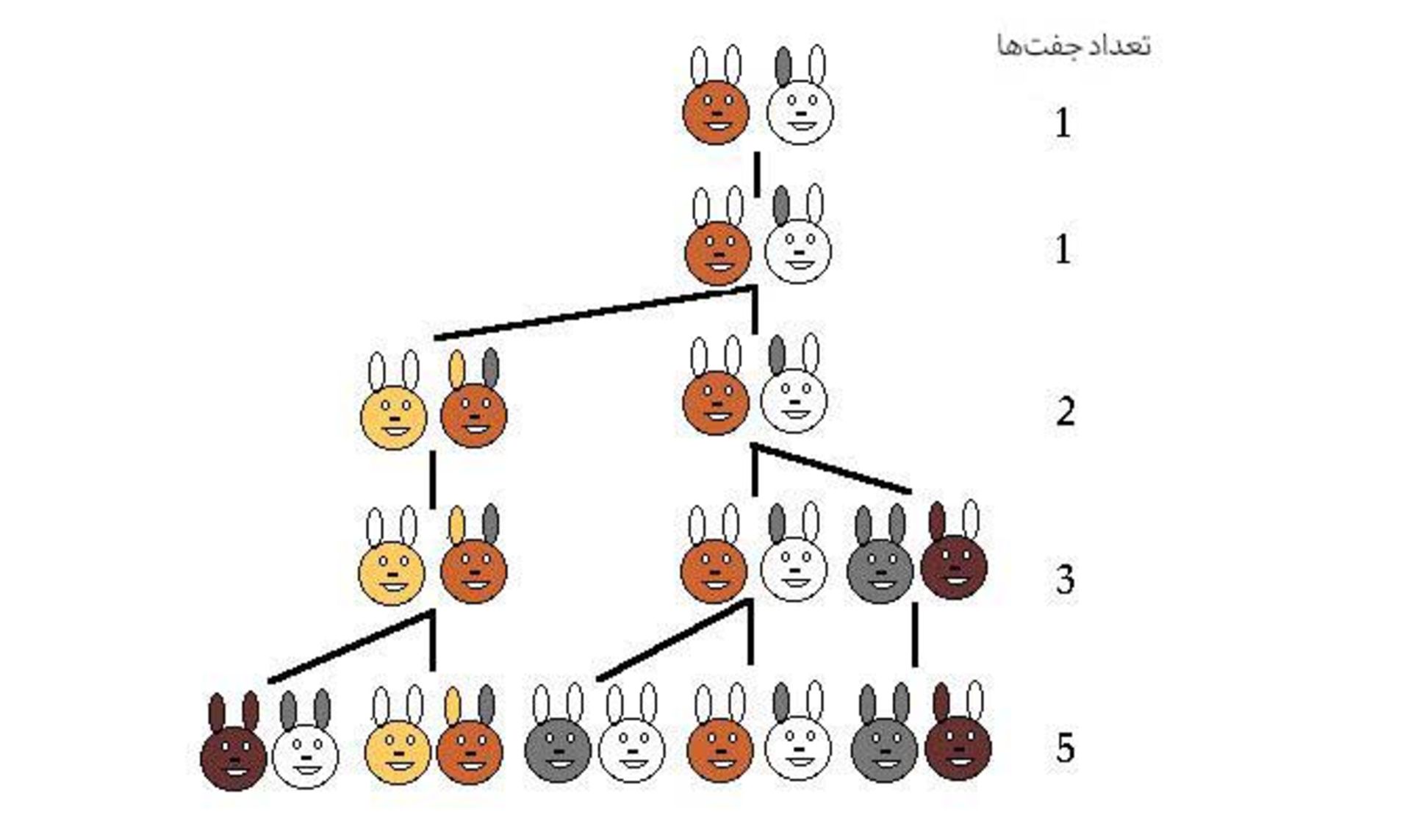
جواب این مسئله ۱۴۴ است. فرمولی که برای رسیدن به این عدد استفاده شد، همان دنباله‌ی فیبوناچی است. بعد از یک سال یا همان ۱۲ ماه، ۱۴۴ جفت خرگوش وجود خواهد داشت. 

کتاب «Liber Abaci»‌ برای اولین‌بار دنباله‌ی فیبوناچی را به دنیای غرب معرفی کرد؛ اما لئوناردو به جز چند پاراگراف کوتاه درباره‌ی زاد و ولد خرگوش‌ها، هیچ جای دیگری درباره‌ی این دنباله صحبت نکرد. در واقع تا مدت‌ها این دنباله به فراموشی سپرده شده بود تا اینکه در قرن نوزدهم، ریاضیدان‌ها ویژگی‌های بیشتری از این دنباله کشف کردند. در سال ۱۸۷۷، ادوارد لوکا، ریاضیدان فرانسوی، به‌طور رسمی مسئله‌ی ریاضی خرگوش‌ها را «دنباله‌ی فیبوناچی» نامید.

نسبت طلایی (golden ratio) رابطه‌ی ریاضی منحصربه‌فردی است که به الگوی فیبوناچی مرتبط است. دو عدد زمانی با یکدیگر نسبت طلایی دارند که نسبت مجموع این دو عدد (a+b) تقسیم بر عدد بزرگ‌تر (a) مساوی نسبت عدد بزرگ‌تر تقسیم بر عدد کوچک‌تر (a/b)‌ باشد. 

نسبت طلایی حدوداً برابر با ۱٫۶۱۸ است و با حرف یونانی فی (Φ) نشان داده می‌شود؛ اما رابطه‌ی نسبت طلایی با دنباله‌ی فیبوناچی چیست؟

نسبت اعداد متوالی فیبوناچی (۲/۱، ۳/۲، ۵/۳ و ...) به مقدار نسبت طلایی نزدیک است. در واقع، هرچه اعداد فیبوناچی بزرگ‌تر باشند، یا به عبارت دیگر هرچه در این دنباله به سمت بی‌نهایت حرکت کنیم، نسبت آن‌ها به ۱٫۶۱۸ یا همان عدد فی نزدیک‌تر می‌شود. از آنجایی که نسبت طلایی به‌وفور در طبیعت یافت می‌شود، به آن «نسبت الهی»‌ نیز می‌گویند.

الگوی دیگری که از دنباله‌ی فیبوناچی مشتق شده است و نمونه‌های بسیاری از آن در اطراف ما یافت می‌شود، مارپیچ طلایی (golden spiral) نام دارد که دور آن مستطیل طلایی شکل می‌گیرد. مارپیچ فیبوناچی یا طلایی مجموعه‌ای از یک از چهارم دایره‌های به هم متصل است که در داخل آرایشی از مربع‌هایی که ابعادشان از اعداد فیبوناچی پیروی می‌کنند، قرار گرفته‌اند. مثلاً تخمه‌های گل آفتابگردان، غلاف‌های بذر میوه‌ی درخت کاج، گل‌کلم و آناناس و حتی شکل برخی تارهای عنکبوت به‌صورت مارپیچ فیبوناچی کنار هم قرار گرفته‌اند.

دنباله‌ی فیبوناچی در زمینه‌های بسیاری کاربرد دارد. علم اقتصاد، به‌خصوص فارکس و بازار سهام و همچنین فیزیک نور به‌دفعات از این دنباله استفاده می‌کنند. این سیستم به‌وفور در طبیعت، از جمله شاخه‌های درختان، مولکول‌های دی‌ان‌ای و حتی کهکشان‌ها دیده می‌شود. نسبت طلایی و دنباله‌ی فیبوناچی در موسیقی نیز کاربرد دارد و حتی روش آهنگسازی خاصی به نام سیستم شیلینگر به استفاده از این دنباله اختصاص یافته است. 

از این دنباله در معماری نیز استفاده می‌شود. معروف‌ترین مثال نسبت طلایی در معماری هرم بزرگ جیزه در مصر است؛ محیط هرم تقسیم بر دو برابر ارتفاع عمودی آن نسبت طلایی به دست می‌دهد (۰٫۶۱۸ برابر پهن‌تر از ارتفاع آن).

اخیرا توجه محققان به کاربردهای این دنباله و نسبت طلایی در حوزه‌های مختلف علمی جلب شده است و از آن در فیزیک انرژی بالا، مکانیک کوانتومی، رمزنگاری داده و کدنویسی استفاده می‌کنند. فیبوناچی در مقیاس مورد استفاده‌ی گروه‌های اسکرام برای ارزیابی کار نیز استفاده می‌شود. در ادامه به‌طور مفصل درباره‌ی کاربرد دنباله‌ی فیبوناچی در طبیعت، موسیقی و فارکس توضیح خواهیم داد.

امروزه، الگوهای مربوط به دامنه‌ی فیبوناچی را می‌توان از مقیاس خرد تا کلان و در سیستم‌های بیولوژیکی تا اشیا بی‌جان مشاهده کرد. نسبت طلایی در تمام ساختارها و الگوهای موجود در جهان قابل مشاهده نیست؛ اما فراوانی آن به‌حدی است که حائز اهمیت باشد. در ادامه به چند نمونه از اعداد فیبوناچی در طبیعت اشاره می‌کنیم:‌

تعداد گلبرگ‌های گل‌ها همواره از دنباله‌ی فیبوناچی پیروی می‌کند. از نمونه‌های معروف می‌توان به گل سوسن با سه گلبرگ، گل آلاله با پنج گلبرگ، کاسنی با ۲۱، گل دیزی با ۳۴ و همین‌طور گل‌هایی با ۵۵ یا ۸۹ گلبرگ اشاره کرد.

علت ظهور مقدار فی در تعداد گلبرگ‌های گل، چینش ایده‌آل برگزیده‌ی فرایندهای داروینی است. هر گلبرگ با درجه‌ی ۰٫۶۱۸۰۳۴ (از ۳۶۰ درجه‌ی دایره) نسبت به گلبرگ کناری خود قرار گرفته تا در بهترین مکان برای دریافت نور خورشید و سایر عوامل قرار گیرد. 

به همین ترتیب، مارپیچ طلایی در چینش تخمه‌های گل آفتابگردان و میوه‌ی درخت کاج قابل مشاهده است. 

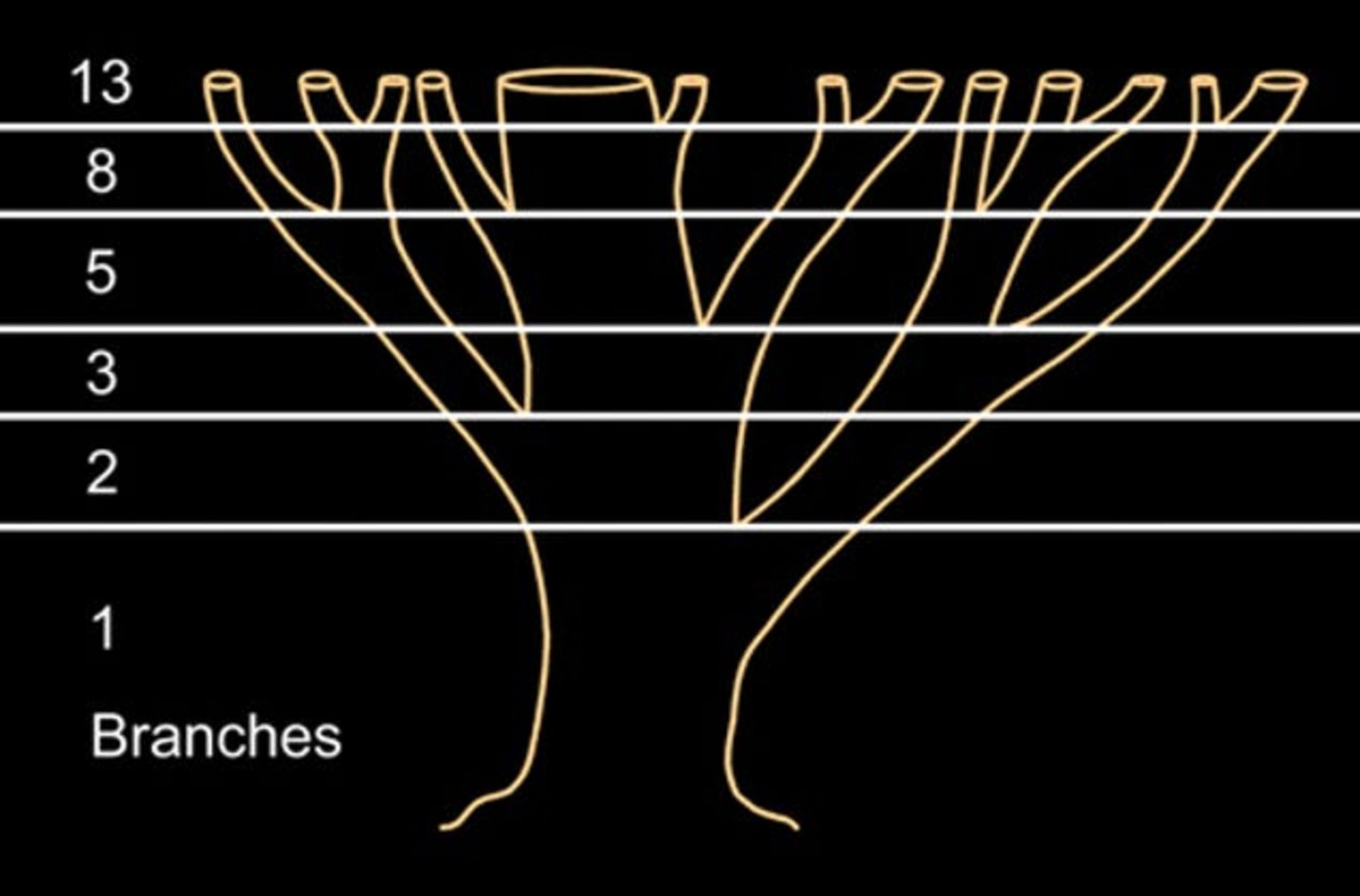
دنباله‌ی فیبوناچی در درخت‌ها از رشد تنه شروع می‌شود و سپس با قد کشیدن درخت، به شکل مارپیچ به سمت بیرون ادامه می‌یابد. نسبت طلایی در شاخه‌های درخت نیز قابل مشاهده است. تنه ابتدا به دو شاخه و بعد یکی از این دو شاخه خود به دو شاخه‌ی دیگر منشعب می‌شود، درحالی‌که که شاخه‌ی دیگر بدون انشعاب باقی می‌ماند. این روند به همین شکل ادامه پیدا می‌کند. سیستم‌های ریشه‌ای و حتی جلبک‌ها نیز از این الگو پیروی می‌کنند.

پوسته‌های ناتیلوس (موجودات دریایی معروف به «فسیل‌های زنده») وقتی برش می‌خورند، مارپیچی لگاریتمی را به نمایش می‌گذارند که از بخش‌های محفظه‌ای تشکیل شده است. هر محفظه‌ی جدید برابر است با اندازه‌ی دو محفظه‌ی قبل از آن که مارپیچ لگاریتمی را ایجاد می‌کند. این رشد متناسب به این دلیل اتفاق می‌افتد که ناتیلوس در طول زندگی خود تا رسیدن به اندازه‌ی کامل با سرعت ثابتی رشد می‌کند.

جای تعجب نیست که کهکشان‌های مارپیچی نیز از الگوی آشنای فیبوناچی پیروی می‌کنند. کهکشان‌های راه شیری، آندرومدا و M81 دارای چندین بازوی مارپیچی هستند که کاملا با مارپیچ فیبوناچی منطبق هستند. 

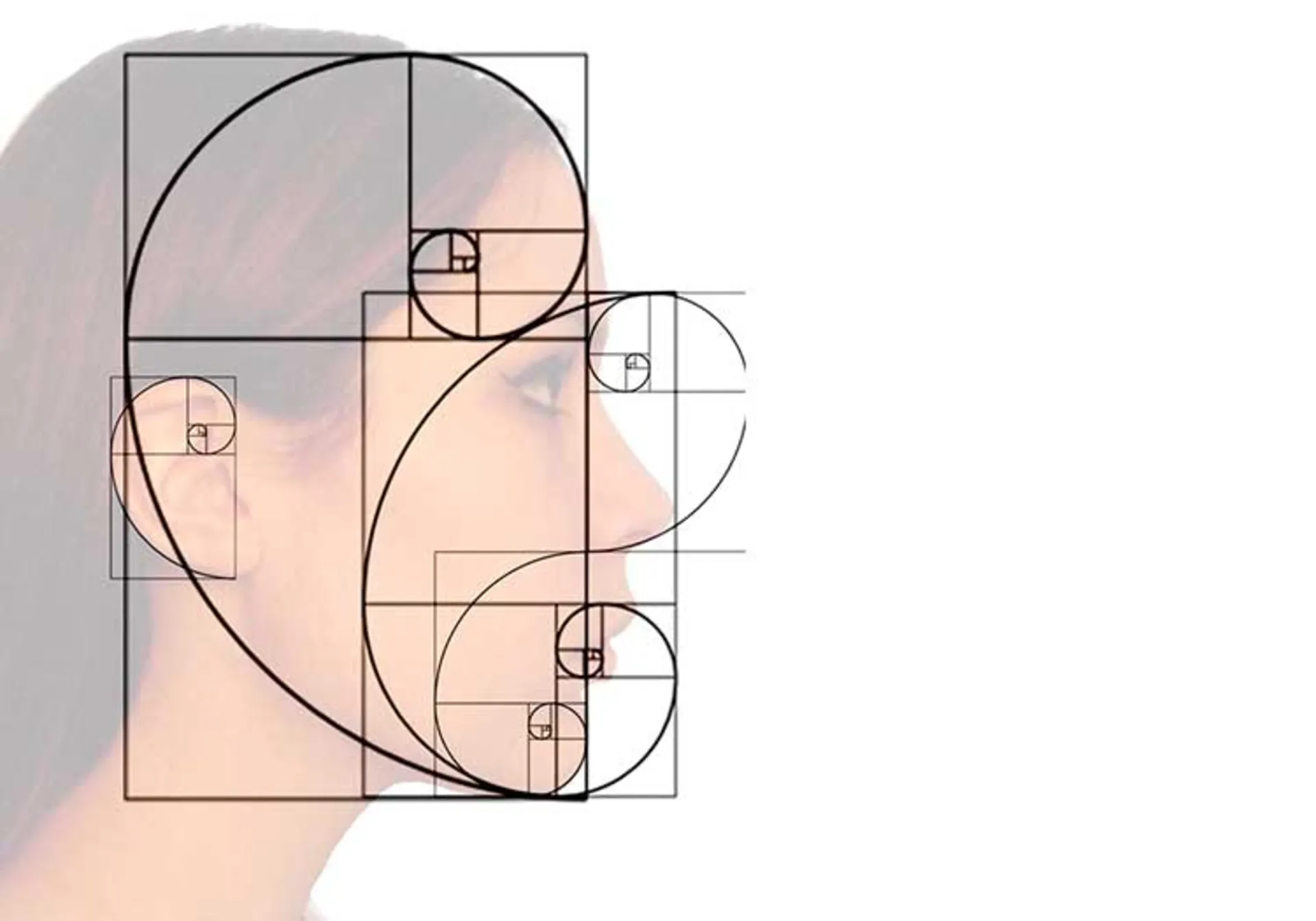
صورت انسان یا غیر انسان مملو از نمونه‌هایی از نسبت طلایی است. فاصله‌ی دهان و بینی با چشم‌ها و پایین چانه هر کدام نسبت طلایی را رعایت کرده است. اگرچه بدن افراد با یکدیگر متفاوت است؛ اما میانگین‌ها همواره به سمت عدد فی مایل هستند. حتی این‌طور گفته شده است که هرچه تناسب اندام فرد به عدد فی نزدیک‌تر باشد، به چشم جذاب‌تر می‌آید.

مثلاً برخی بر این باورند زیباترین لبخندها آن‌هایی هستند که در آن دندان‌های جلویی به نسبت ۱٫۶۱۸ پهن‌تر از دندان‌های کناری هستند که آن‌ها هم به نسبت ۱٫۶۱۸ از دندان‌های نیش پهن‌تر هستند. نظریه‌ای وجود دارد که می‌گوید انسان‌ها به‌گونه‌ای تکامل یافته‌اند که از فرم‌هایی که از نسبت طلایی پیروی می‌کنند، بیشتر خوششان بیاید.

زنبورهای عسل از بسیاری جهات از دنباله‌ی فیبوناچی پیروی می‌کنند. برجسته‌ترین مثال، تقسیم تعداد زنبورهای ماده‌ی یک کندو بر تعداد زنبورهای نر است (ماده‌ها همیشه از نرها بیشترند) که معمولا عددی نزدیک به ۱٫۶۱۸، یعنی نسبت طلایی، به دست می‌آید. 

بعلاوه، شجره‌نامه‌ی زنبورهای عسل نیز از این الگو پیروی می‌کند. نرها فقط یک مادر دارند، درحالی‌که ماده‌ها هم پدر و هم مادر دارند. در نتیجه، در این نسب‌نامه نرها ۲، ۳، ۵ و ۸ جد دارند و به همین ترتیب زنبورهای ماده هم ۲، ۳، ۵، ۸، ۱۳ و الی آخر. حتی فیزیولوژی زنبورها هم به زیبایی از منحنی طلایی پیروی می‌کند.

حتی دنیای میکروسکوپی نیز از دنباله‌ی فیبوناچی در امان نیست. مولکول DNA برای هر چرخه‌ی کامل از مارپیچ دو‌تایی خود، ۳۴ آنگستروم (۱۰ به توان -۱۰ متر) طول و ۲۱ آنگستروم عرض دارد. این اعداد ۳۴ و ۲۱ از سری فیبوناچی هستند و نسبت آن‌ها ۱٫۶۱۹۰۴۷۶ و نزدیک به عدد فی است.

در آثار نوابغی چون موتزارت و لئوناردو داوینچی، نمونه‌هایی از دنباله‌ی فیبوناچی مشهود است؛ اما کسی نمی‌داند چرا استفاده از این دنباله باعث ایجاد موسیقی گوش‌نوازتر یا نقاشی دل‌انگیزتری می‌شود.

وقتی از اعداد دنباله فیبوناچی مربع می‌سازیم و این مربع‌ها را به شکل مستطیلی کنار هم قرار می‌دهیم و گوشه‌های مربع‌ها را به هم وصل می‌کنیم، به مارپیچ زیبایی به این شکل می‌رسیم: 

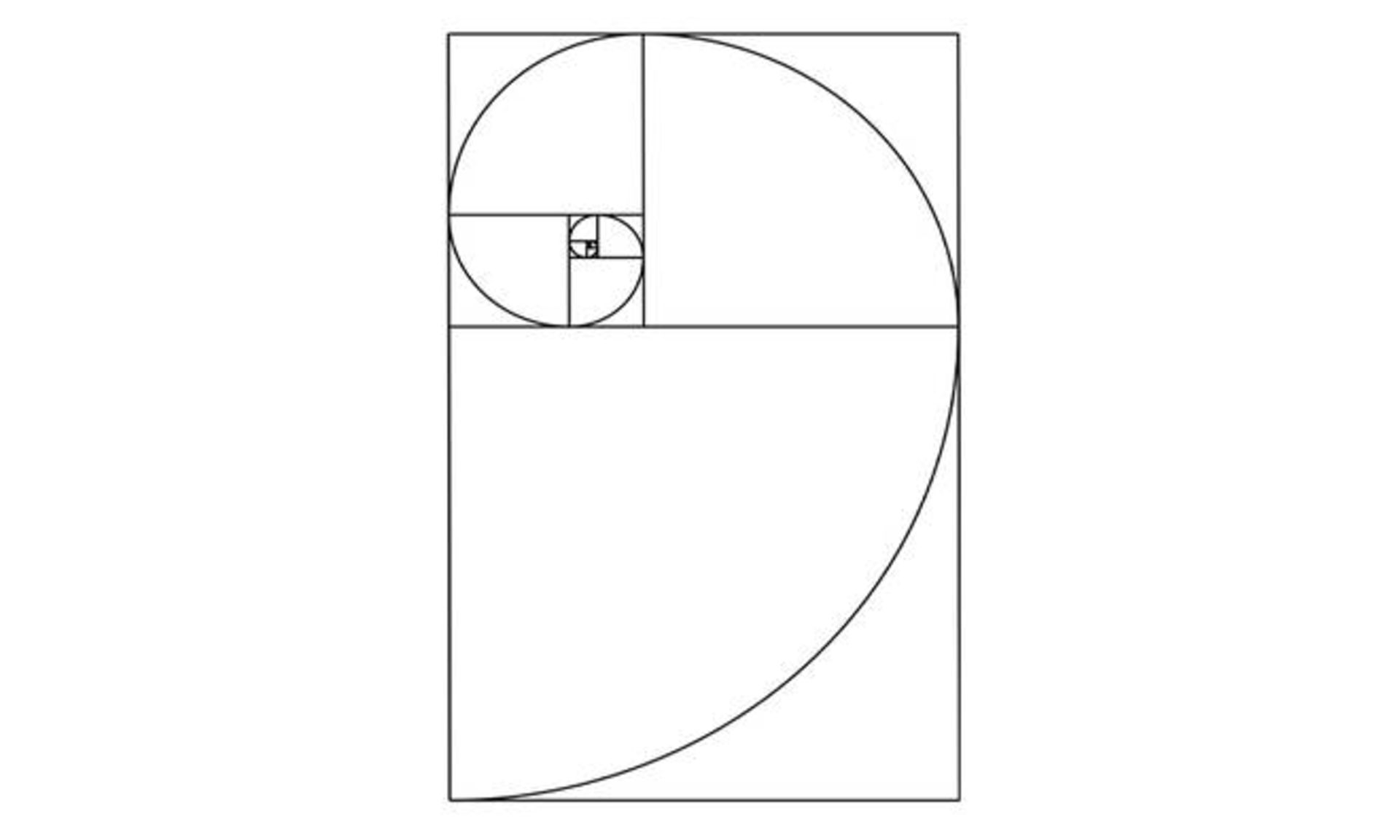
آشنا به نظر می‌رسد؟ احتمالا آن را قبلا جایی دیده باشید …

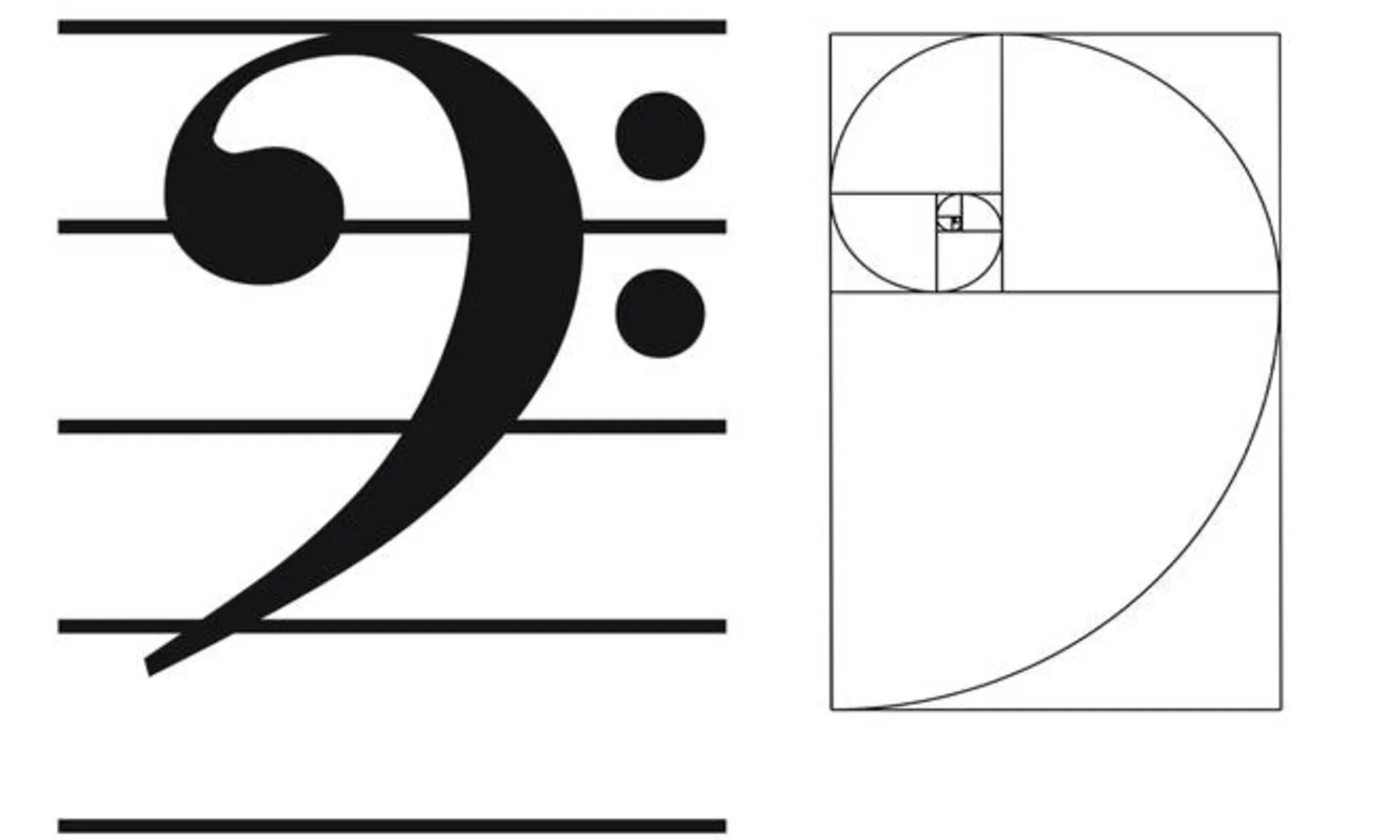
این دنباله، الگو و شکل مارپیچ در نمونه‌های بسیاری که احتمالا تا حالا به آن توجه نکرده‌اید، دیده می‌شوند. به نقاشی مونا لیزا اثر لئوناردو داوینچی دقت کنید. شکل مارپیچ فیبوناچی در آن مشهود است:

دنباله‌ی فیبوناچی در موسیقی غربی و گام‌های موسیقی نقش بزرگی ایفا می‌کند. به این موارد دقت کنید:‌

• یک اکتاو پیانو شامل ۱۵ نوت است که از بین آن‌ها ۸ کلید سفید و ۵ کلید سیاه هستند. 
• هر گام از ۸ نوت تشکیل ‌شده است که نوت سوم و پنجم اساس آکورد پایه را می‌سازند.
• در هر گام، نوت غالب، نوت پنجم است که هشتمین نوت در ۱۳ نوت سازنده‌ی اکتاو نیز است. 
• ۸ تقسیم بر ۱۳ برابر است با ۰٫۶۱۵۳۸، تقریبا برابر با نسبت طلایی.

تمام این اعداد مطرح‌شده (۳،۵،۸،۱۳) از دنباله‌ی فیبوناچی هستند. 

موتزارت بسیاری از آثار خود، به‌خصوص سونات‌های پیانو را بر اساس نسبت طلایی ساخته است. کارشناسان حوزه‌ی موسیقی مدعی هستند بتهوون، بلا بارتوک، کلاد دبوسی، فرانتس شوبرت، باخ و اریک ساتی هم از این تکنیک برای نوشتن سونات‌های خود استفاده کردند؛ اما کسی نمی‌داند چرا استفاده از این تکنیک در موسیقی موفقیت‌آمیز بوده است. 

نسبت طلایی همچنین در ساخت ویولن، دهنی ساکسیفون، سیم‌های بلندگو و حتی در طراحی آکوستیک برخی از کلیساها به کار رفته است.

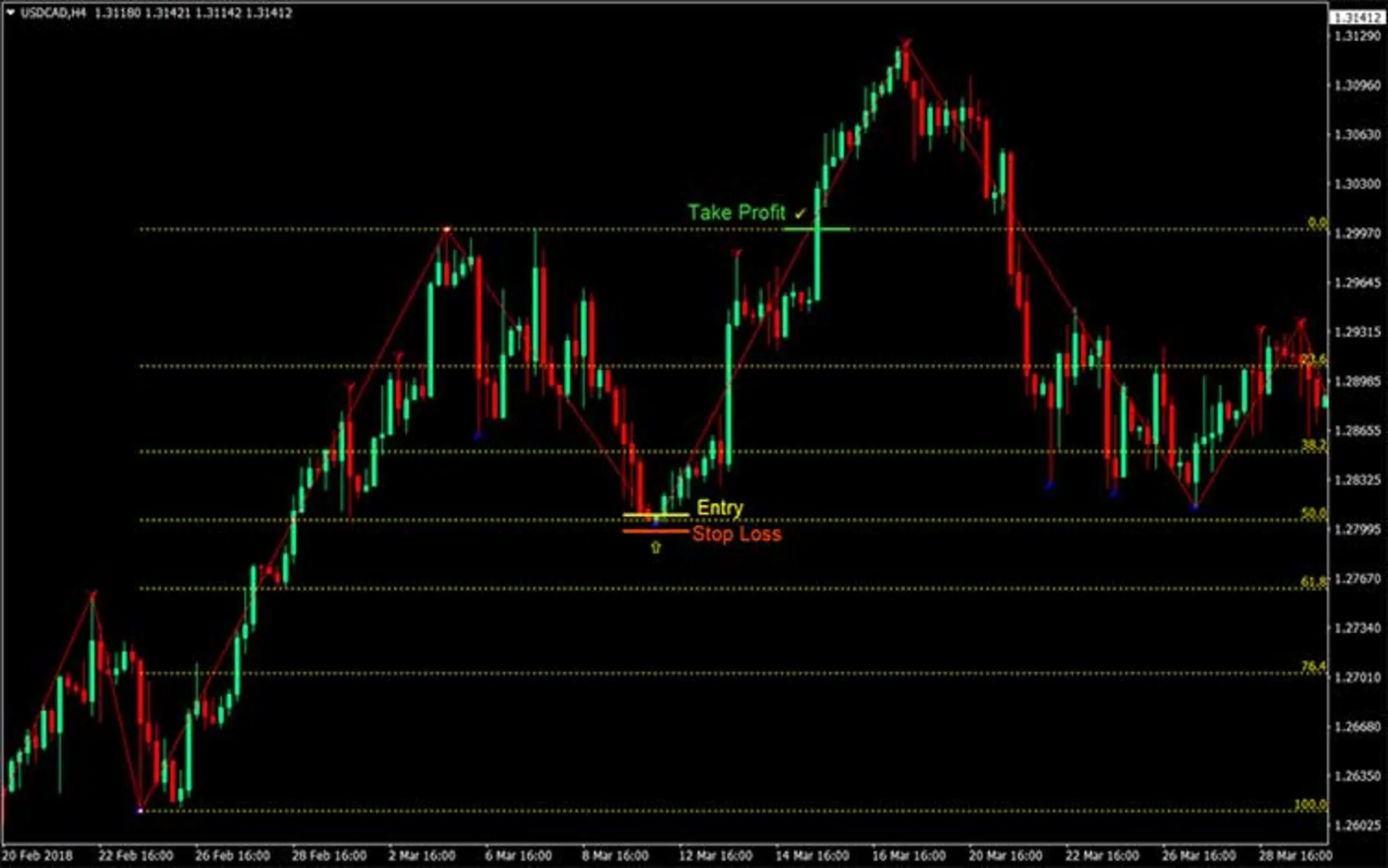
از اعداد فیبوناچی همچنین در تحلیل تکنیکال (Technical Analysis) برای پیش‌بینی قیمت و ورود به بازار بورس اوراق بهادار، بازار ارز و فارکس و نیز بازارهای بورس کالا استفاده می‌شود.

 بسیاری از تحلیلگران معتقدند به کمک ابزار فیبوناچی، از جمله فیبوناچی اصلاحی (retracement) و فیبوناچی انبساطی (extension)، می‌توان رفتار بازار را در ۷۰ درصد موارد با موفقیت پیش‌بینی کرد. تحلیلگران از این ابزار برای تعیین نقاط ورود و خروج و محاسبه‌ی محدوده‌ی حمایت یا مقاومت استفاده می‌کنند.

مثلاً در فیبوناچی اصلاحی، از اعداد ۲۳٫۶ درصد، ۳۸٫۲ درصد، ۶۱٫۸ درصد، ۷۸٫۶ درصد استفاده می‌شود که همگی نسبت‌هایی هستند که از دنباله‌ی فیبوناچی به دست آمده‌اند؛ به این صورت که نسبت هر عدد فیبوناچی به عدد بعدی ۰٫۶۱۸، به دومین عدد جلویی ۰٫۳۸۲ و به سومین عدد جلویی، ۰٫۲۳۶ است. 

در تحلیل تکنیکال، فیبوناچی اصلاحی مقدار بازگشت پول را محاسبه می‌کند و فیبوناچی انبساطی یا گسترشی، میزان حرکت موج اصلی قیمت را نشان می‌دهد. این ابزارها در اکثر موارد به این خاطر در پیش‌بینی خود موفق عمل می‌کنند که معامله‌گران بسیاری با دقت این محدوده‌ها را نظاره می‌کنند تا برای دستیابی به بیشترین سود، خرید و فروش انجام دهند.

بسیاری از نرم‌افزارهای رسم نمودار از محدوده‌ی ابزار فیبوناچی اصلاحی و انبساطی استفاده می‌کنند. 

نسبت طلایی تمایل طبیعت به مؤثرترین و کم‌مصرف‌ترین چینش ممکن را مدل‌سازی می‌کند. مثلاً در مورد تخمه‌های آفتابگردان یا بسیاری از گونه‌های گیاهی دیگر، چینشی که از نسبت طلایی پیروی می‌کند درواقع ایده‌آل‌ترین حالت ممکن را به نمایش می‌گذارد تا در مرکز تراکم بیش از حد و در گوشه‌ها تراکم کم ایجاد نشود. به همین ترتیب، تعداد گلبرگ‌های هر گل و قرار گرفتن آن‌ها در کنار هم به‌گونه‌ای است که بهترین میزان آفتاب به آن‌ها برسد. این الگوهای منظم نتیجه‌ی سیر تکامل طی میلیون‌ها سال است و بهینه‌ترین چینش را برای هرگونه‌ی جانوری به نمایش می‌گذارد. 

در مورد جنبه‌های اسرارآمیز دنباله‌ی فیبوناچی باید این نکته را در نظر داشت که این طبیعت نیست که آگاهانه از قوانین ریاضی پیروی می‌کند؛ بلکه این قوانین ریاضی است که از طبیعت پیروی می‌کنند. 

به همین خاطر، بسیاری از دانشمندان معتقدند دنباله‌ی فیبوناچی اسرار مخفی طبیعت نیست؛ این الگوهای تکرارشونده همان داستان آشنای تکامل است؛ اما باور به این موضوع چیزی از زیبایی این دنباله و هیجان کشف آن در طبیعت و دنیای اطراف ما و کنجکاوی درباره‌ی علت آن کم نمی‌کند. به قول آرتور بنجامین، ریاضی تنها یافتن جواب مسئله نیست، بلکه یافتن دلیل آن نیز است.

شما کاربر زومیت درباره‌ی دنباله‌ی فیبوناچی چه فکر می‌کنید؟ آیا این الگو واقعا به این اندازه که گفته می‌شود، در طبیعت تکرار شده است یا ذهن انسان عادت دارد در هر چیزی الگو پیدا کند؟