فیزیک فضاپیماهای چرخان؛ سکونتگاه‌های دارای گرانش مصنوعی چه مشکلاتی دارند؟

درحالی‌که توانایی زندگی در فضا برای بسیاری افراد ایده‌ای عالی و جالب به‌نظر می‌آید، مواجهه با محیط «بدون وزن» مشکلاتی جدی ایجاد می‌کند. بدن انسان در سطح زمین و در جایی که تحت‌تأثیر نیروی گرانشی ثابت قرار می‌گیرد، بهترین عملکرد را دارد؛ درحالی‌که قرارگرفتن طولانی‌مدت درمعرض ریزگرانش، عواقب شناخته‌شده‌ای ازجمله کاهش توده استخوانی و آتروفی عضلانی در پی خواهد داشت. درنتیجه، برای زندگی در فضا باید یک محیط گرانشی مصنوعی ایجاد کنیم.

ما برای انجام چنین کاری فقط یک روش داریم: ساخت وسیله‌ای که با شتاب ثابت حرکت می‌کند. در‌این‌میان، رایج‌ترین طرح مفهومی به ایجاد فضاپیمایی مربوط است که به‌صورت چرخشی یا اسپینی کار می‌کند. بااین‌حال، واقعیت این است که ساخت چنین فضاپیماهایی به آن راحتی نیست که در نگاه نخست به‌نظر می‌رسد.

ابتدا به اصول گرانش و معنای احساس وزن در انسان می‌پردازیم. گرانش به کشش بین اجسام دارای جرم گفته می‌شود. ازآن‌جاکه هم بدن ما و هم زمین جرم دارند، نیروی جذب‌کننده‌ای وجود دارد که ما را به‌سمت زمین می‌کشد و روی آن نگه می‌دارد. حتی با اینکه نیروی یادشده دائماً روی شما تأثیر می‌گذارد؛ ولی آن را احساس نمی‌کنید؛ چرا؟ بدین‌دلیل که زمین هم‌زمان تمام قسمت‌های بدن را به‌سوی خود می‌کشد و این اثر را تشخیص‌ناپذیر می‌کند.

برخی افراد در مواجهه با توضیحات یادشده پاسخی تک‌خطی و متداول ارائه می‌دهند: «من این‌جا روی صندلی‌ خودم نشسته‌ام و وزنم را کاملاً احساس می‌کنم.» واقعیت این است آنچه احساس می‌کنید، جاذبه نیست؛ بلکه فشار وارده‌ی صندلی و زمین به بدنتان است. این نیروی واردشده به‌سمت بالا را در فیزیک به‌عنوان وزن ظاهری فرد در نظر می‌گیرند.

ما با سفری سریع در آسانسور می‌توانیم مفهوم وزن ظاهری را درک کنیم. آسانسوری را تصور کنید که در حالت سکون شروع به کار می‌کند. در‌ادامه و با فشرده‌شدن دکمه‌ای، شروع به حرکت به‌سمت بالا می‌کند؛ یعنی به‌تعبیری باید شتابی رو به بالا داشته باشد. این شتاب دست‌کم برای مدت‌زمان بسیار کوتاه و تا زمان رسیدن آسانسور به سرعت حرکت مدنظر، وجود خواهد داشت.

در طول این شتاب رو به بالا، سرنشینان کمی احساس سنگینی می‌کنند. احتمالاً شما نیز با حس مشابهی در برخی آسانسورها رو‌به‌رو بوده‌اید. پس از این مرحله و هنگامی‌که آسانسور به طبقه‌ی برنامه‌ریزی‌شده‌ی مقصد نزدیک می‌شود، باید سرعتش را کاهش دهد. در این مرحله، آسانسور باید در جهت پایین شتاب بگیرد. در این مدت کوتاه، سرنشینان نوعی احساس سبکی را تجربه خواهند کرد.

طبعاً می‌دانیم که وزن واقعی فرد در این مراحل هرگز نوسانی نداشته است. وزن واقعی ما، معیاری است از میزان نیرویی که گرانش به بدن وارد می‌کند. وزن واقعی را به‌عنوان نتیجه‌ی برهم‌کنش بین جرم فرد (m) با جرم زمین و فاصله‌ی او از مرکز زمین تعریف می‌کنند. روی زمین نیروی گرانشی برابر با ۹/۸ نیوتن به‌ازای هر یک کیلوگرم وارد می‌شود. علاوه‌براین، می‌دانیم که جرم و وزن چیزهای متفاوتی هستند و در سیاره‌ای با گرانش متفاوت، وزن فرد مقدار متفاوتی خواهد بود.

سوارشدن بر آسانسور هیچ‌یک از عوامل یادشده در بند بالا را تغییر نمی‌دهد و تنها چیزی که دستخوش تغییر می‌شود، وزن ظاهری است. شاید اندکی عجیب به‌نظر برسد؛ اما واقعیت این است که چنین اثری برای فضاپیما بسیار کاربردی است.

فرض کنید در فضایی باشید که گرانشی در آن‌جا وجود ندارد. بیایید فرضمان را کمی ملموس‌تر کنیم: مدار پایین زمین؛ محیطی که ریزگرانش در آن حکم‌فرما است. عبارت «ریزگرانش» درواقع نامی است که ما به محیط «بدون وزن» نسبت می‌دهیم. حال پرسش این است که اگر فضاپیمای فرضی شما آسانسور عظیمی می‌داشت که دائماً به‌سمت بالا شتاب می‌گرفت، چه اتفاقی می‌افتاد؟ اگر شتاب آن آسانسور به‌اندازه‌ی میدان گرانشی روی سطح زمین بود، وزنتان دقیقاً به‌شکل حالت فعلی روی زمین احساس می‌شد.

ایده‌ی سفینه‌ی فضایی با آسانسور بی‌نهایت غیرعملی است. راهکار ساده‌تر این خواهد بود که کل وسیله‌ی فضایی شتاب بگیرد. چنین شتابی گرانش مصنوعی ایجاد می‌کند. اگر از دنبال‌کنندگان آثار علمی‌تخیلی باشید، احتمالاً به‌یاد می‌آورید که روش مذکور درواقع روش اصلی به‌کار‌رفته در کشتی‌های فضایی در سریال علمی‌تخیلی The Expanse بود.

مسئله این است که درعمل برای اینکه فضاپیما به‌طورمداوم شتاب بگیرد، باید پیشرانه‌هایش را همواره روشن نگه دارد. بدیهی است که چنین ایده‌ای به مقادیر غیرعادی سوخت موشک نیاز خواهد داشت. افزون‌براین، این نکته را باید مدنظر گرفت که امکان خاموش‌کردن پیشرانه‌ها وجود ندارد؛ زیرا انجام چنین کاری شتاب فضاپیما را به صفر خواهد رساند. ناسلامتی می‌خواهیم گرانش مصنوعی داشته باشیم!

در سریال The Expanse، این مشکل را با اختراع «رانشگر اپشتین» که نوعی موشک فیوژن است، حل کردند. چنین ایده‌ای در دنیای واقعی بیشتر شبیه جادو به‌نظر می‌رسد. ما انسان‌های عصر حاضر با ابزارهای کنونی برای تولید گرانش مصنوعی، به روشی جز شتاب خطی نیاز داریم.

شتاب را به‌عنوان نرخ تغییر سرعت تعریف می‌کنند. برای مثال، اگر خودرویی در مدت یک ثانیه از سرعت ۱۰ متربرثانیه به ۲۰ متربرثانیه برسد، آن خودرو شتاب ۱۰ متر بر مجذورثانیه خواهد داشت. در این‌جا باید توجه کنیم که سرعت در‌واقع یک بردار است؛ یعنی سرعت نه‌تنها درباره‌ی کمّیّت سرعت حرکت یک جسم، بلکه درباره‌ی «جهت» حرکت آن نیز اطلاعاتی به‌ ما می‌دهد.

فرض کنید ماشینی با سرعت ۲۰ متربرثانیه در حال حرکت به‌سمت غرب است. این ماشین در‌ادامه به‌طوری گردش می‌کند که پس از یک ثانیه، با سرعت ۲۰ متر‌بر‌ثانیه به‌سمت شمال در حرکت باشد. در این‌‌جا با اینکه ماشین با همان سرعت حرکت می‌کند، به‌دلیل تغییر جهت، شتابی را تجربه کرده است. اگر شعاع (R) مسیری که ماشین در این پیچ می‌پیماید و سرعت آن را (v) بدانیم، می‌توانیم مقدار شتاب را محاسبه کنیم.

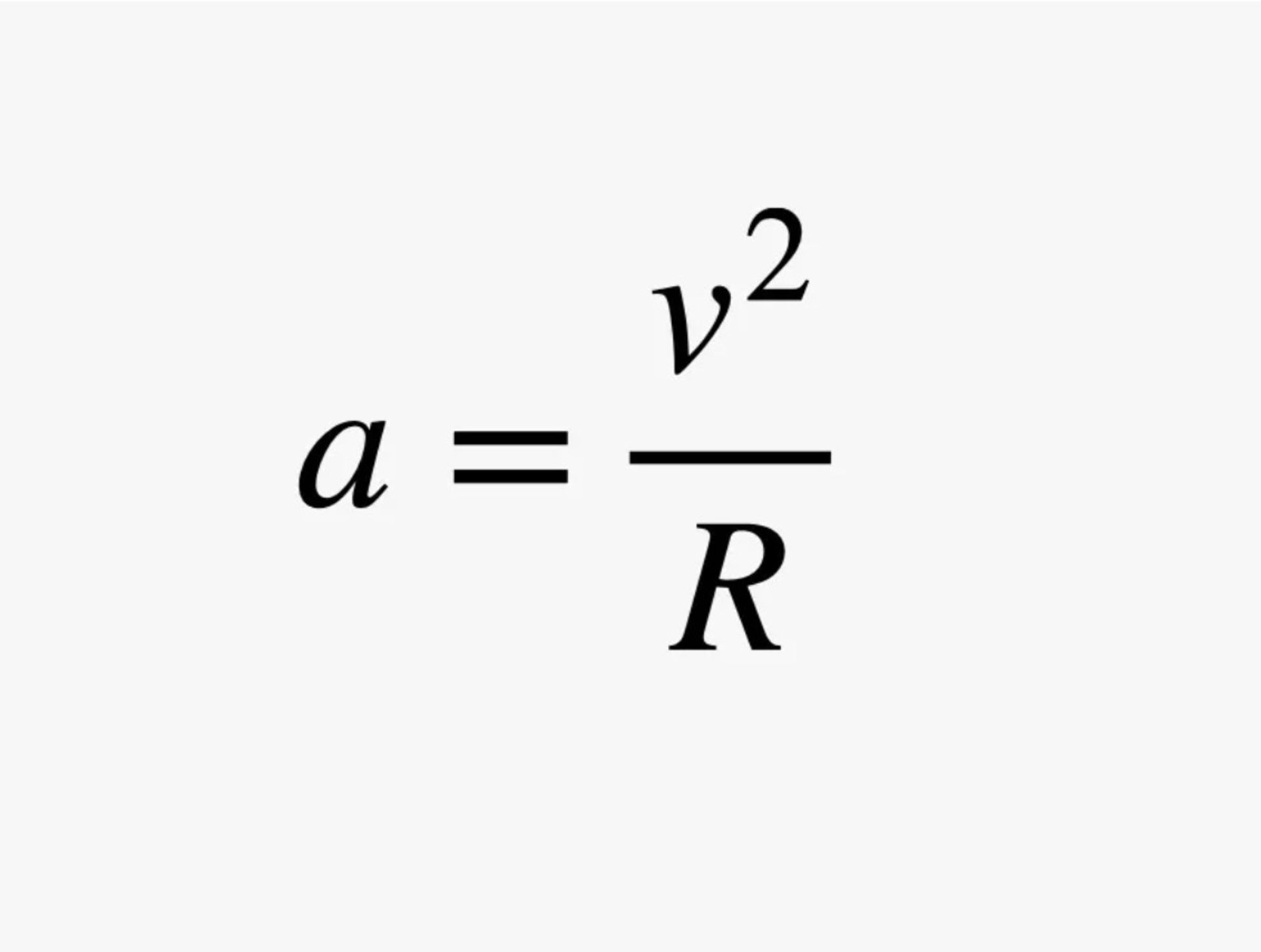
واقعیت این است که فرد برای درک مفهوم چنین شتابی لزوماً به دانستن روابط ریاضی یادشده نیازی ندارد. پیش‌از‌این نیز به‌طورشهودی پی برده‌ایم که «چرخش» رخ‌داده در ماشین نوعی شتاب است؛ زیرا می‌توان هُل‌داده‌شدن به کناره‌های ماشین را حین چرخش خودرو احساس کرد. شتاب در آسانسور در حال حرکت را نیز می‌توان به‌ شیوه‌ای مشابه احساس کرد.

پس از کنارگذاشتن ایده‌ی آسانسور بی‌نهایت و اشاره به ایده‌ی شتاب حین چرخش خودرو، این ایده به ذهن خطور می‌کند که شاید بتوانیم از جسمی چرخشی برای ایجاد شتاب مصنوعی بهره ببریم. برای اجرای این ایده، لزوماً نیازی نیست که فضاپیما یا ایستگاه فضایی را به‌شکلی دایره‌ای و مانند ماشین ذکرشده در مثال فوق بچرخانیم. به‌جای آن، جسم چرخان بزرگی را تصور کنید که افراد داخل آن ایستاده اند. این ایده مانند تصویر زیر خواهد بود:

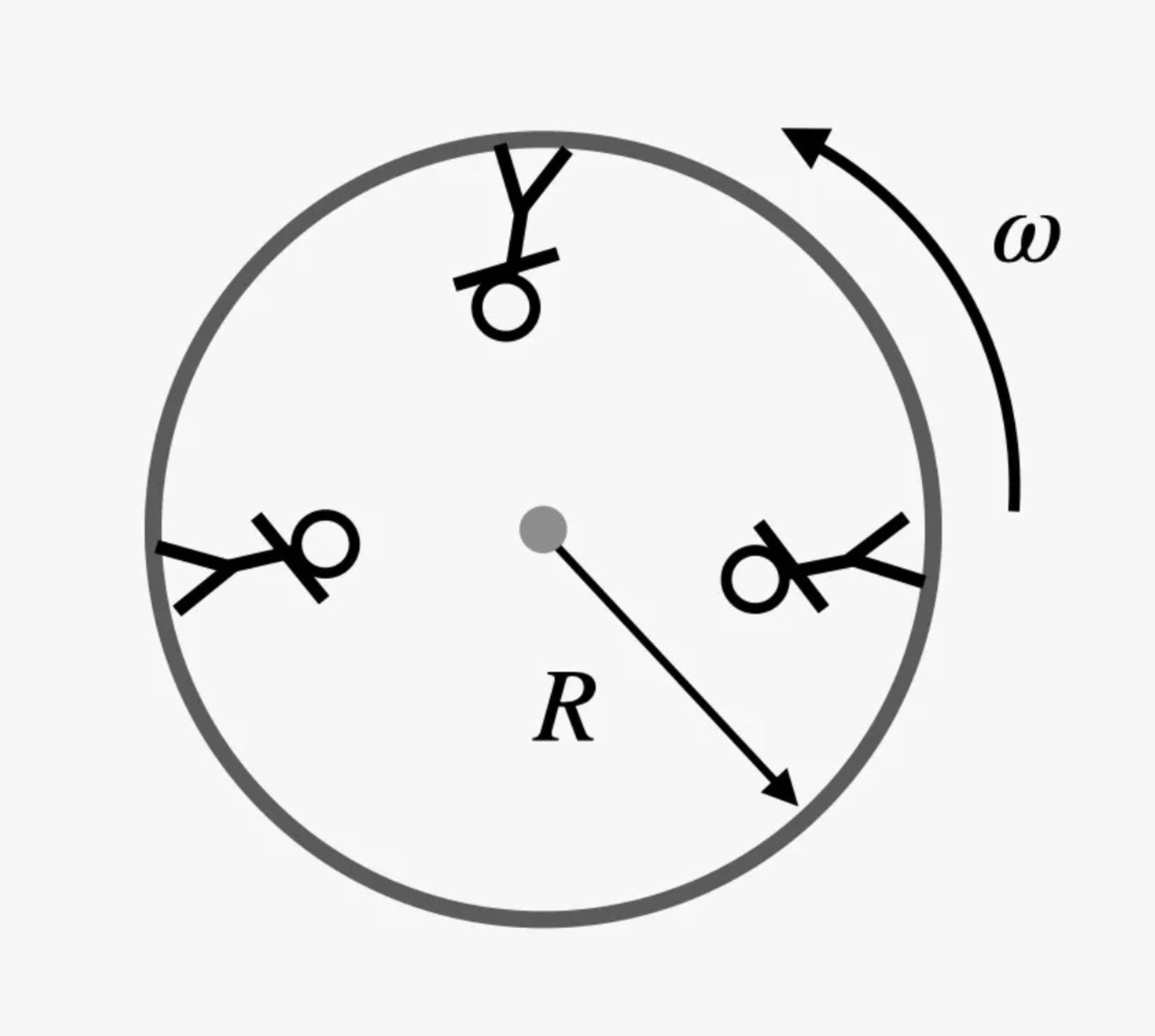
در این‌جا، سه نفر درون استوانه‌ای چرخان ایستاده‌اند. ازآن‌جاکه همه‌ی آن‌ها در مسیرهای دایر‌ه‌ای حرکت می‌کنند، هرکدامشان شتابی دارند و اثری شبیه گرانش را احساس می‌کنند. برای آنان، جهت «بالا»، به‌سمت مرکز استوانه است. به‌نظر می‌رسد که می‌توانیم حرکت آن‌ها را به‌جای سرعت (v)، با سرعت زاویه‌ای فضاپیما (ω) توصیف کنیم. با این کار، هر فرد شتابی معادل با رابطه زیر خواهد داشت:

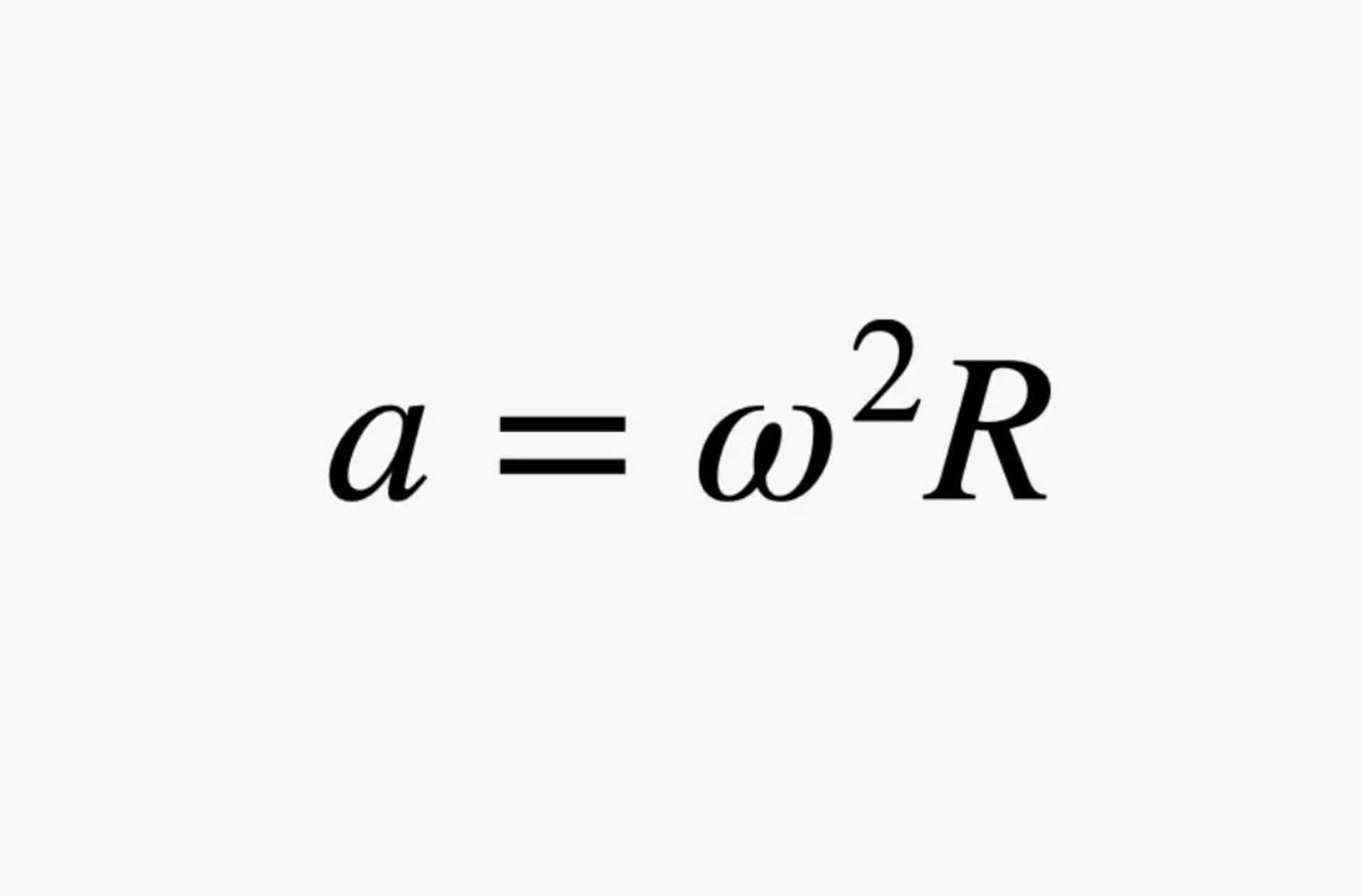
سرعت زاویه‌ای (ω) برحسب رادیان‌برثانیه اندازه‌گیری می‌شود. اگر این شتاب مقدار ۹٫۸ متربرمجذورثانیه (همان میدان گرانشی روی سطح زمین) داشته باشد، شخص درون استوانه تقریباً احساسی مثل احساس قرار‌گرفتن روی سطح سیاره‌مان خواهد داشت. به قید «تقریباً» در این جمله دقت کنید. در‌ادامه، به اختلافات میان دو حالت اشاره خواهیم کرد.

نکته‌ی مثبت درباره‌ی سفینه‌ی فضایی یا ایستگاه فضایی چرخان این است که پس از به چرخش درآمدن آن، دیگر به استفاده از سوخت موشک برای ادامه‌ی کار نیازی نخواهد بود و تا زمانی‌که چیزی جلو چرخشش را نگیرد، به چرخش ادامه خواهد داد. به‌همین‌دلیل، این روش برای ایجاد گرانش مصنوعی در سریال‌های تلویزیونی علمی‌تخیلی و فیلم‌هایی مانند بابیلون ۵، مریخی، میان‌ستاره‌ای و ادیسه فضایی و بسیاری آثار دیگر مشاهده می‌شود.

علاوه‌براین، معادله‌ی مذکور نکته‌ی مهمی برای طراحی سفینه‌ی فضایی در خود دارد: می‌توان وسیله‌ای کوچک (با یک R کوچک) ساخت و آن را به‌طور بسیار سریع (با ω بزرگ) چرخاند یا اینکه کشتی فضایی بزرگی با سرعت چرخش کم ایجاد کرد.

با کاهش شعاع فضاپیمای در حال چرخش، سرعت زاویه‌ای باید افزایش یابد تا درنهایت شتاب مدنظر حاصل شود (فرض کنیم ۹/۸ متربرمجذورثانیه؛ این معادل 1g، یعنی شتابی معادل با ایستادن روی سطح زمین خواهد بود). باوجوداین، دوباره مشکلی وجود خواهد داشت و مسئله این بار نه موشک‌ها یا هزینه‌ها و زیرساخت‌های فنی، بلکه انسان‌ها هستند.

احتمالاً درست حدس زده‌اید: ما با چرخش مشکل داریم. به این فکر کنید که تعداد زیادی از ما انسان‌ها نمی‌توانیم بدون دردسر از عهده‌ی هیچ‌یک از سواری‌های چرخشی در شهربازی‌ها بر‌بیایم! حتی شاید فکر‌کردن به برخی از آن سازه‌های شهربازی نیز برخی افراد را دچار استرس کند.

براساس دستاوردهای آزمایشگاهی، اکثر افراد می‌توانند نرخ چرخش حدود یک دوربردقیقه را تحمل کنند. داده‌های دیگر نشان می‌دهد که سرعت زاویه‌ای تا ۴ دوربردقیقه نیز برای برخی تحمل‌پذیر است. در مطالعه‌ای دیگر، با قرار‌دادن انسان‌ها درمعرض دوره‌های فزاینده‌ی سرعت چرخشی بیشتر، معلوم شد که شاید انسان‌ها بتوانند تا ۲۶ دوربردقیقه را هم تاب آورند.

فرض کنیم فضانوردانی داریم که می‌توانند سرعت چرخش ۲۶ دور در دقیقه را تحمل کنند. در آن صورت، برای ایجاد گرانش مصنوعی معادل 1g، کوچک‌ترین فضاپیمای ممکن چه ابعادی خواهد داشت؟ برای محاسبه‌ی ساده‌ی پاسخ این پرسش، ابتدا باید سرعت زاویه‌ای را از دور‌بر‌دقیقه به رادیان‌‌بر‌ثانیه تبدیل کنیم. این مقدار ω معادل ۲/۷۲ رادیان‌برثانیه است.

درادامه، فقط از شتاب ۹٫۸ متربرمجذورثانیه استفاده و R (شعاع) را پیدا می‌کنیم. محاسبات ما را به فضاپیمایی دایره‌ای با شعاع ۱٫۳ متر و قطر ۲٫۶ متر خواهد رساند که بسیار کوچک است. این اندازه حتی از قطر یک ماژول ایستگاه فضایی بین‌المللی با اندازه حدود ۴٫۲ متر نیز کمتر است. اگر با سرعت زاویه‌ای معقول‌تر، یعنی ۴ دوربردقیقه، حرکت کنیم، قطر فضاپیمای موردنیاز این بار به ۱۱۲ متر خواهد رسید که بسیار بزرگ‌تر از عدد قبلی، به‌اندازه‌ی زمین فوتبال است.

درصورت تمایل‌نداشتن به ساخت سفینه‌ی فضایی عظیم و دوّار با قطر ۱۱۲ متر، ترفند جایگزین کوچکی وجود دارد که شاید ارزش بررسی داشته باشد. به‌جای جسمی بزرگ، می‌توان از دو جسم کوچک‌تر استفاده و آن‌ها را با کابل به‌هم وصل کرد. این دو بخش کوچک‌تر در‌ادامه حول یک مرکز جرم مشترک می‌چرخند. می‌توان انسان‌ها را در یکی یا هر دو این قسمت‌ها قرار داد تا آن‌ها بتوانند میدان گرانشی مصنوعی را تجربه کنند. نمونه‌ای از این نوع کشتی‌های دوّار در فیلم Stowaway از نتفلیکس مشاهده شد.

بااین‌حال، دو اتفاق می‌تواند در فضاپیمای در حال چرخش رخ دهد که موجب شود بفهمید روی سطح زمین نیستید. شاید میدان گرانشی مصنوعی در سر فرد مقدار متفاوتی با قدرت میدان در پای او داشته باشد. برای پی‌بردن به چرایی این اتفاق، فردی را در نظر بگیریم که در فضاپیمایی نسبتاً کوچک در حال چرخش ایستاده است.

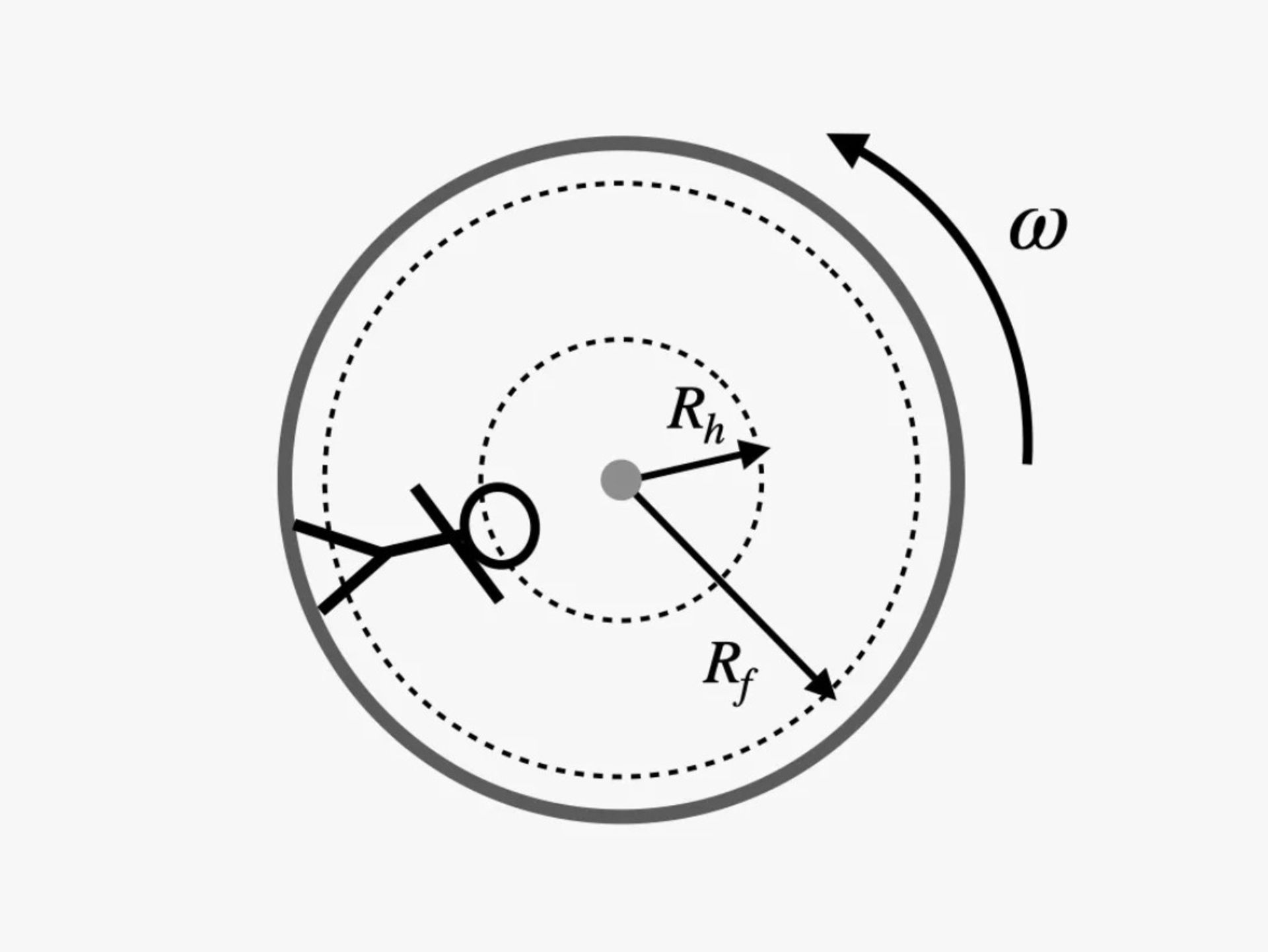
ازآن‌جاکه فرد حاضر در این مثال در وسیله‌ای در حال چرخش است، سر و پاهای او سرعت زاویه‌ای (ω) یکسانی خواهند داشت. بااین‌حال، آن‌ها در دایره‌های هم‌اندازه حرکت نمی‌کنند. سر فرد درمقایسه‌با پاهایش، به مرکز محفظه‌ی دوّار نزدیک‌تر است؛ به‌طوری‌که شعاع مسیر دایره‌ای سر (Rh) کوچک‌تر از شعاع مسیر مشابه (Rf) برای پاها خواهد بود. فراموش نکنید که مقدار شتاب و درنتیجه گرانش مصنوعی با شعاع حرکت کاهش می‌یابد. از این موضوع نتیجه می‌گیریم که سر فرد درمقایسه‌با پاهایش میدان گرانشی کوچک‌تری را تجربه خواهد کرد و این پدیده کمی عجیب است.

عجیب‌بودن ماجرا به همین‌جا ختم نمی‌شود و اوضاع برای بدن انسان حتی می‌تواند بدتر از این هم باشد. آن فضاپیمای بسیار کوچک با شعاع فقط ۱/۳ متر را تصور کنید. این شعاع از قد فردی معمولی کوتاه‌تر است و درنتیجه، می‌تواند سر فضانورد را از مرکز چرخش عبور دهد. در چنین حالتی، سر انسان‌های حاضر در محفظه‌ی دوّار به یک سمت از فضاپیما (به‌عنوان قرارداد آن را «سقف» می‌نامیم) و پاهایشان به‌سوی دیگر (کف) کشیده می‌شود. حتی اگر چرخش واقعاً سریع محفظه برای به‌هم‌زدن حال جسمانی این فضانورد کافی نباشد، این گرانش مصنوعی عجیب مطمئناً ازپسِ انجام آن وظیفه برخواهد آمد!

اگر قد فضانوردی ۱۷۵ سانتی‌متر باشد، سر او در شعاع دایره‌ای ۵۴/۱ متری حرکت می‌کند؛ یعنی میدان گرانشی در سر فرد برابر با ۹/۴۹ متربرمجذورثانیه خواهد بود. اختلاف میان شتاب تجربه‌شده در سر و پای سرنشینان حدود ۳/۲ درصد می‌شود و اساساً مقدار درخورتوجه یا مشکل‌سازی نیست.

حضور در سفینه‌ی فضایی چرخان پیامد دیگری نیز دارد که به آن نیروی کوریولیس می‌گویند. ماهیت این نیرو پیچیده است. در این‌جا با مثالی با استفاده از چرخ‌و‌‌فلک چرخان موضوع را تشریح می‌کنیم. فرض کنید دو نفر (با برچسب A و B) روی این چرخ‌و‌فلک ایستاده‌اند: یکی در لبه و دیگری نزدیک‌تر به وسط. در این‌جا یک نمای بالا از نحوه‌ی قرارگیری آن‌ها وجود دارد:

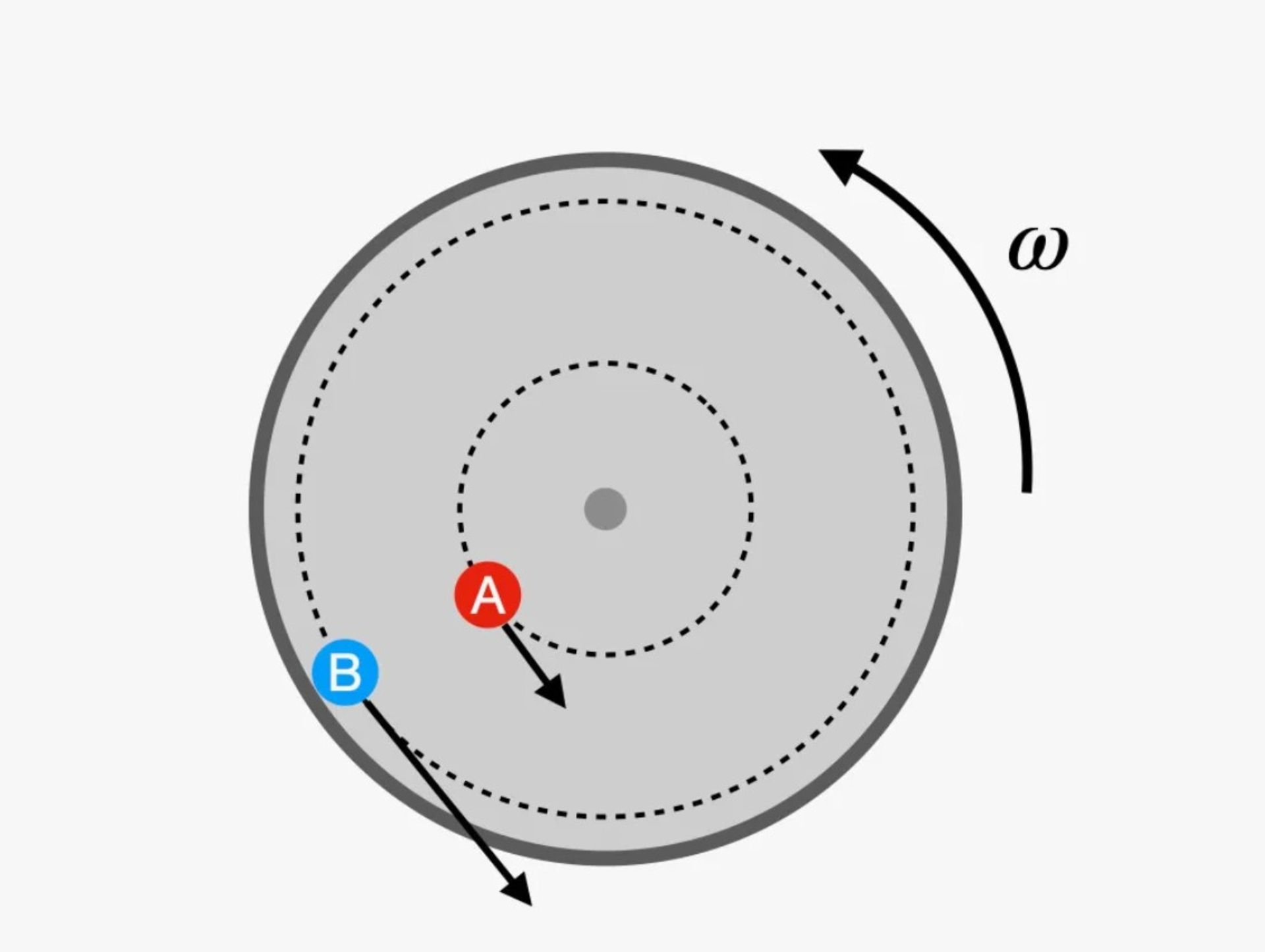
توجه کنید که هر دو نفر در مسیرهای دایره‌ای با سرعت زاویه‌ای یکسان حرکت می‌کنند. بااین‌حال، شخص B برای کامل‌کردن یک دور کامل باید مسافت بیشتری را در زمان مشابه بپیماید. این بدان‌معنا است که B سرعت خطی (v) بیشتری از A خواهد داشت.

این مسئله به‌خودی خود چندان مهم نیست؛ مشکل از جایی شروع می‌شود که شخص B تصمیم بگیرد به‌سمت مرکز دایره حرکت کند. شخص B با حرکت به مسیر دایره‌ای جدید با شعاع کوچک‌تر، حرکتی بیش‌از‌حد سریع را در قواره‌ی آن شعاع جدید تجربه خواهد کرد. سرعت بیشتر در این شعاع دایره‌ای جدید بدان‌معنا است که مسیر این فرد به‌سمت کناره‌ انحنا پیدا خواهد کرد.

نیروی اضافی تشریح‌شده در این مثال، نیروی کوریولیس نامیده می‌شود. اگر شخص B توپی را به‌سمت شخص A بغلتاند، این توپ در یک مسیر منحنی خواهد غلتید؛ مانند تصویر زیر:

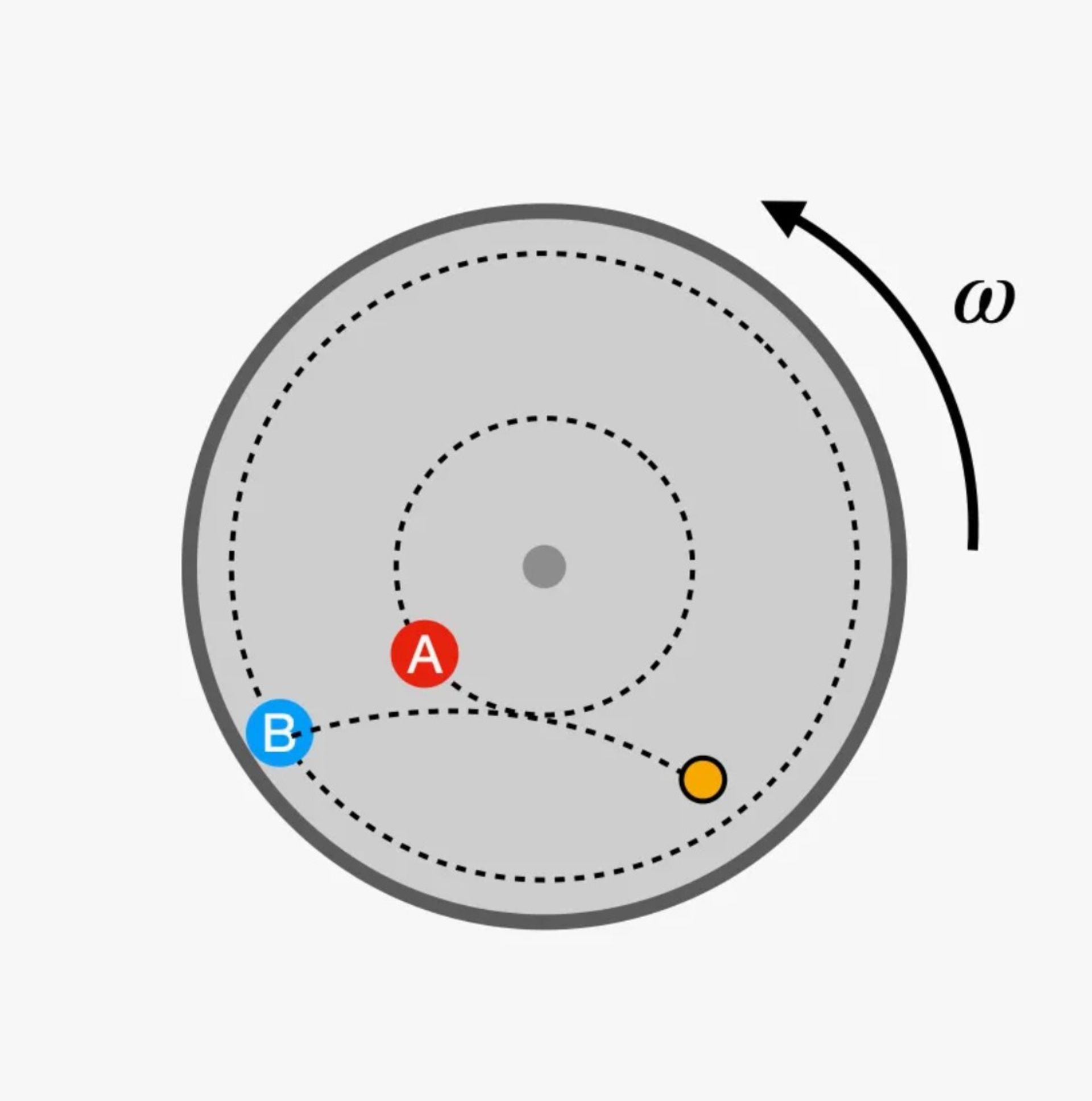
بزرگی نیروی کوریولیس هم به سرعت جسم متحرک (با‌توجه‌به قاب در حال چرخش) و هم به سرعت زاویه‌ای چرخ‌و‌فلک در حال چرخش بستگی دارد و همین اتفاق در فضاپیما نیز رخ می‌دهد. عوامل زیادی وجود دارد که محاسبه‌ی نیروی کوریولیس را پیچیده می‌کند؛ اما آن را به‌عنوان معادله‌‌ای به‌صورت زیر می‌توانیم بنویسیم:

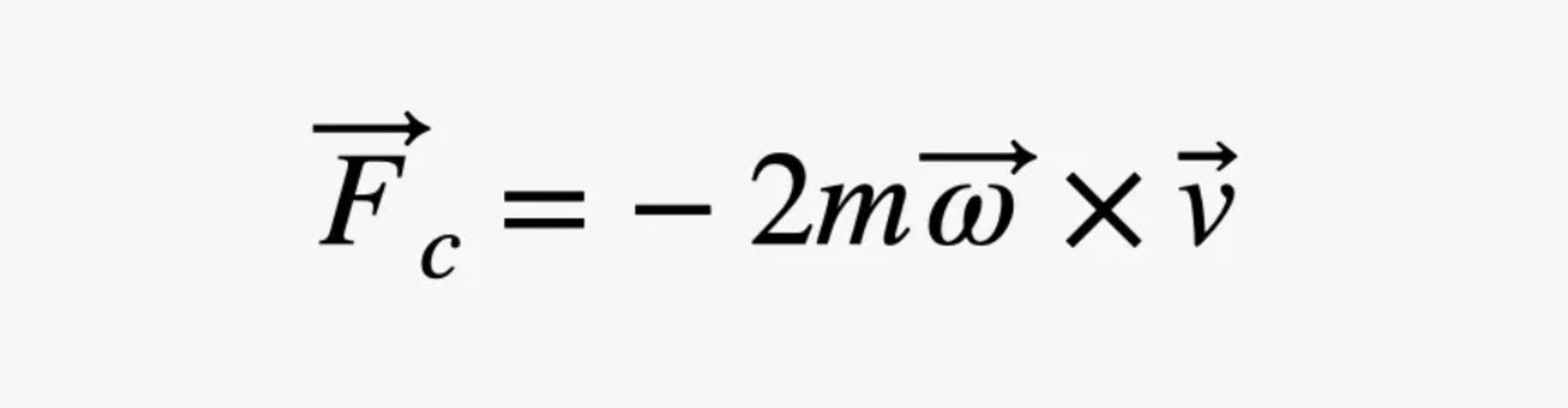
باید توجه کنیم که این نیرو همیشه عمود بر سرعت است و اگر جسم در قاب چرخان ساکن باشد، نیروی کوریولیس صفر خواهد شد. حال پرسش این است که نیروی مذکور چه بر سر فضانورد حاضر در فضاپیمای در حال چرخش خواهد آورد؟

اگر فرد فقط بنشیند و حرکتی نکند، هیچ اتفاقی نمی‌افتد؛ اما اگر بخواهد از حالت نشسته به حالت ایستاده تغییر موضع دهد، چه می‌شود؟ در طول فرایند ایستادن، سرعت فرد به‌سمت مرکز دایره خواهد بود. دلیل این امر آن است که مرکز جرم فرد در حال تغییر حالت از نشسته به ایستاده، به‌سمت بالا حرکت می‌کند.

نیروی کوریولیس آن‌ها را متناسب با سرعتشان به‌سمت طرفین فشار خواهد داد و بسته به جهت صندلی، این نیرو می‌تواند آن‌ها را به جهات مختلف هُل دهد. اگر جهت صندلی و جهت فضاپیمای در حال چرخش یکی باشد، نیروی کوریولیس شخص ایستاده درون فضاپیما را به‌سمت جلو هُل خواهد داد. اگر جهت صندلی رو به عقب باشد، شخص ایستاده نیز به عقب هل داده می‌شود. اگر صندلی رو به دیوار کناره‌ی محفظه باشد، سرنشینان به‌سوی یکدیگر هُل داده خواهند شد.

موضوع تنها به ایستادن خلاصه نمی‌شود. این نیرو در مواقعی که سرنشین قصد انجام حرکات کوچک‌تر را داشته باشد، هم خود را نشان خواهد داد. برای مثال، اگر سرنشین فضاپیما دست خود را حرکت دهد، نیرویی جانبی به آن وارد خواهد شد یا فرضاً اگر بخواهد مقداری نوشیدنی را در لیوان بریزد، بازهم همواره نیرویی جانبی به مایع وارد خواهد آمد. شاید این‌گونه به ذهن متبادر شود که سرنشینان می‌توانند برای هر حرکتی خودشان را با نیرویی جانبی وفق دهند؛ اما به‌نظر می‌آید که این وضعیت بسیار آزاردهنده خواهد بود.

پرسش اساسی این است که آیا می‌توان کار خاصی درباره‌ی نیروی کوریولیس انجام داد؟ پاسخ مثبت است. دانشمندان این گزینه را دارند که با طراحی فضاپیمایی با سرعت زاویه‌ای کمتر، این نیروی هُل‌دهنده به طرفین را به‌حداقل برسانند. بدین‌ترتیب، تکمیل یک چرخش مدت‌زمان بیشتری به طول خواهد انجامید؛ اما این به‌معنای گرانش مصنوعی کمتر است.

اگر بخواهیم فضاپیما گرانش مصنوعی شبیه زمین و اثر کاهش‌یافته‌ی کوریولیس داشته باشد، فقط به سفینه‌ی فضایی بزرگ‌تر نیاز خواهیم داشت. انتخاب سختی است: می‌توان فضاپیمایی کوچک و ارزان ساخت و با نیروهای آزاردهنده کوریولیس مواجه شد یا می‌توان سفینه‌ی فضایی بزرگ و گران‌قیمتی با تمام امکانات ساخت. پرواضح است که حالت دوم بسیار گران‌تر خواهد بود.