هندسه کثیفی که حدس دیرینه کاشی‌کاری را نقض کرد

هنرمندان و هندسه‌دان‌ها از دوران باستان به این پرسش فکر کردند که چگونه می‌توان با یک شکل کل صفحه را بدون شکاف یا همپوشانی کاشی‌کاری کرد. به گفته‌ی الکس یوسویچ، ریاضی‌دان دانشگاه راچستر پژوهشگرها به پاسخی برای این پرسش رسیدند.

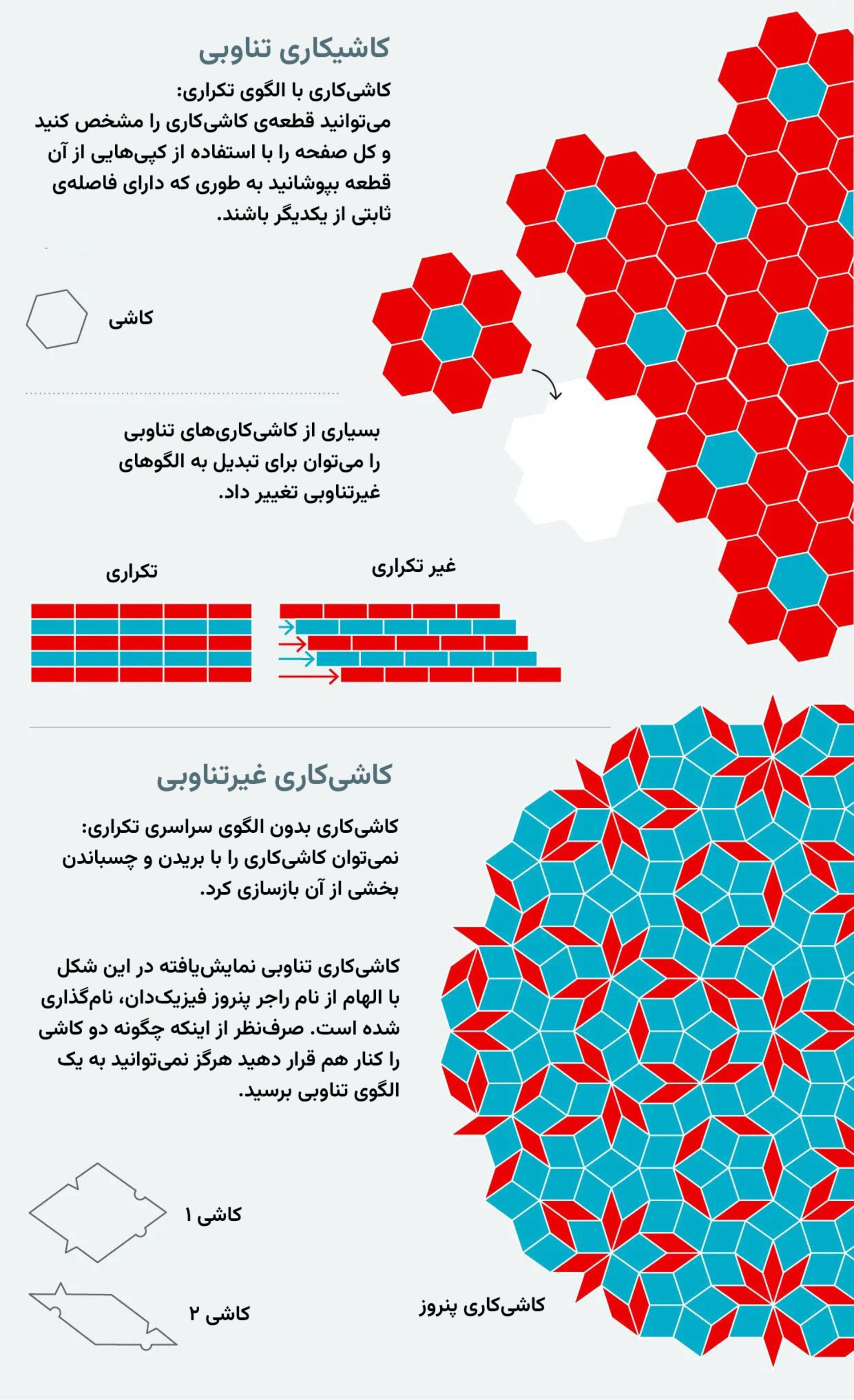
بر اساس یک قانون کلی، واضح‌ترین کاشی‌ها تکرار می‌شوند: به‌راحتی می‌توان یک سطح با مربع‌ها، مثلث‌ها یا شش‌ضلعی‌های تکراری پوشاند. ریاضی‌دان‌ها در دهه‌ی ۱۹۶۰ به مجموعه‌های عجیبی از کاشی‌ها رسیدند که می‌توانند به‌طور کامل یک صفحه را بپوشانند اما به‌گونه‌ای که هرگز تکرار نشوند.

اولین الگوی غیرتکراری یا غیرتناوبی شامل مجموعه‌ای از ۲۰٬۴۲۶ کاشی متفاوت بود. ریاضی‌دان‌ها می‌خواستند بدانند آیا می‌توان این تعداد را کاهش داد. راجر پنروز که همچنین برنده‌ی جایزه‌ی نوبل فیزیک ۲۰۲۰ برای کار روی سیاه‌چاله‌ها بود، در اواسط دهه‌ی ۱۹۷۰ ثابت کرد مجموعه‌ی ساده‌ای از دو کاشی لوزی‌شکل که اصطلاحا «بادبادک» و «دارت» نامیده می‌شوند برای حل این مسئله کافی هستند.

رسیدن به الگوهای غیرتکراری کار دشواری نیست. بسیاری از کاشی‌کاری‌های تناوبی یا تکراری را می‌توان برای رسیدن به شکل‌های غیرتکراری تغییر داد. برای مثال شبکه‌ای نامتناهی از مربع‌ها را در نظر بگیرید که روی یک تخته‌ی شطرنج مرتب شده‌اند. اگر هر سطح را به گونه‌ای جابه‌جا کنید که بر اساس یک فاصله‌ی ثابت از سطر بالایی تنظیم شود، هیچ منطقه‌ای را پیدا نمی‌کنید که بتوان آن را برید و مانند مهر از آن برای بازسازی کاشی‌کاری استفاده کرد. ترفند واقعی، یافتن مجموعه‌ای از کاشی‌های مشابه پنروز است که بتوانند کل صفحه را بپوشانند به‌طوری‌که هرگز تکرار نشوند.

دو کاشی پنروز این پرسش را به وجود آوردند: آیا کاشی واحدی وجود دارد که در این مثال صدق کند؟ در کمال شگفتی، پاسخ به این پرسش در صورت وجود این شرایط مثبت است: مجاز به جابه‌جایی، چرخاندن یا بازتاب‌دادن کاشی باشید و کاشی ناهم‌بند باشد، به طوری که شکاف‌هایی داشته باشد. این شکاف‌ها را می‌توان با کپی‌های متقارن و چرخانده‌شده‌ای از کاشی پر کرد و در نهایت یک صفحه‌ی کامل دوبعدی را پوشاند؛ اما اگر نتوان این شکل را چرخاند غیرممکن است که بتوان صفحه را بدون به جا گذاشتن شکاف کاشی‌کاری کرد.

چند سال پیش ریاضی‌دانی به نام سیدارتا باتاچاریا ثابت کرد صرف‌نظر از پیچیده بودن یک طراحی موزاییکی، اگر صرفا از جابه‌جایی یا تبدیل یک کاشی مشخص استفاده کنید، غیرممکن است بتوانید موزاییکی بسازید که کل صفحه را به شکل غیرتناوبی بپوشاند.

به باور ریاضی‌دان‌ها، نتیجه‌ی دوبعدی باتاچاریا می‌تواند در فضاهایی با ابعاد بالاتر هم صدق کند. در واقع همان‌گونه که هیچ موزاییک دوبعدی غیرتناوبی وجود ندارد، می‌توان نتیجه گرفت که هیچ بلوک سه‌بعدی مناسبی به این صورت وجود ندارد و به این ترتیب این حدس را برای تعداد بعدهای بیشتر هم اعمال کرد.

به گزارش وایرد، گرینفلد و ترنس تائو از UCLA در پژوهشی جدید این حدس را حل کردند؛ اما آن‌ها از روشی که ریاضی‌دان‌ها پیش‌بینی کرده بودند، استفاده نکردند. بلکه موزاییکی ساختند که بتواند به صورت غیرتناوبی فضایی با ابعاد بالاتر را بپوشاند اما نتواند این کار را به‌صورت تناوبی انجام دهد. به این ترتیب حدس نقض می‌شود. این کاشی عجیب نه‌تنها به خاطر برداشتن مرز ممکن‌ها و غیرممکن‌های هندسی شایسته‌ی توجه است، بلکه به پرسش‌هایی فراتر از هندسه مثل محدودیت‌های منطق ربط دارد.

گرینفلد در سال ۲۰۱۹، به عنوان پژوهشگر پسادکترا در UCLA مشغول به کار شد. او و تائو که هر دو به‌صورت مستقل روی مسئله‌ای مرتبط با کاشی‌کاری‌های تبدیلی کار می‌کردند، دیدگاه‌هایی را برای اثبات حدس کاشی‌کاری تناوبی ارائه دادند.

تائو و گرینفلد، از زمان اثبات حدس کاشی‌کاری تناوبی در یک یا دو بعد، به دنبال اثبات آن در سه بعد بودند. آن‌ها می‌خواستند ثابت کنند اگر بتوان کپی‌هایی از یک شکل را برای کاشی‌کاری کل فضایی سه‌بعدی جابه‌جا کرد، آنگاه روشی هم برای کاشی‌کاری فضا به‌صورت تناوبی وجود خواهد داشت.

پژوهشگران در این راه به پیشرفت‌هایی هم رسیدند، برای مثال حدس را مجددا در دو بعد با استفاده از روش‌های مختلف اثبات کردند که امیدوار بودند یکی از این روش‌ها برای نمونه‌ی سه‌بعدی هم قابل پیاده‌سازی باشد؛ اما ناگهان متوقف شدند. به گفته‌ی تائو آن‌ها در یک مرحله‌ی کار احساس ناامیدی کردند و با خود گفتند خب حتما دلیلی وجود دارد که نمی‌توانیم این حدس را در ابعاد بالاتر اثبات کنیم. پس باید به دنبال مثال‌های نقض باشیم.

پژوهشگرها در پژوهش‌های قبلی به دنبال ساختارهای غیرتکراری رفتند. یکی از این بررسی‌ها که در سال ۱۹۶۴ منتشر شد، مجموعه‌ای با بیش از ۲۰ هزار موزاییک را معرفی می‌کند که می‌توانند از طریق تبدیل‌ها یک سطح را به‌صورت غیرتناوبی بپوشانند. سپس آن‌ها به دنبال توسعه‌ی روش‌های جدیدی برای ساخت یک موزاییک غیرتناوبی رفتند.

پژوهشگرها کار خود را با تغییر مقداردهی شروع کردند. برای مثال فرض کنید بخواهید فضایی دوبعدی را کاشی‌کاری کنید. به‌جای تلاش برای موزاییک کردن یک فضای پیوسته، یک شبکه‌ی توری دوبعدی را در نظر بگیرید که آرایه‌ای نامتناهی از نقاط مرتب‌شده در یک شبکه است. می‌توانید یک کاشی را به شکل مجموعه‌ای متناهی از نقاط روی چنین شبکه‌ای تعریف کنید. اگر کاشی‌کاری را به روشی صحیح انجام دهید، می‌توانید هر نقطه در شبکه‌ را دقیقا با ساخت کپی‌هایی از مجموعه‌ی متناهی از نقاط و سپس لغزاندن آن‌ها به اطراف بپوشانید.

اثبات حدس کاشی‌کاری تناوبی «گسسته» برای شبکه‌هایی با ابعاد بالاتر کمی با اثبات نسخه‌ی پیوسته‌ی این حدس متفاوت است، زیرا کاشی‌کاری‌هایی در شبکه‌ها وجود دارند که در فضای پیوسته‌ای قرار ندارند، بلکه صرفا به یکدیگر ربط دارند. گرینفلد و تائو تلاش کردند مثال نقض گسسته را برای حدس ارائه دهند تا بعدا بتوانند آن را بر نمونه‌ی پیوسته هم اعمال کنند.

تائو و گرینفلد در تابستان ۲۰۲۱ به راه‌حل نزدیک شدند و دو کاشی در فضایی با ابعاد زیاد را پیدا کردند. این موزاییک‌ها می‌توانند فضا را به شکل غیرتناوبی پر کنند. البته به گفته‌ی گرینفلد این کافی نیست. کاشی‌کاری با دو موزاییک انسجام کمتری نسبت به کاشی‌کاری با یک موزاییک دارد؛ بنابراین تقریبا یک سال و نیم دیگر طول کشید تا آن‌ها بتوانند به مثال نقض واقعی برای حدس کاشی‌کاری تناوبی برسند.

آن‌ها کار را با ساخت زبانی جدید و بازنویسی مسئله‌ی خود به‌عنوان شکل خاصی از معادله آغاز کردند. متغیر ناشناخته در این معادله (متغیر لازم برای حل معادله) تمام روش‌های محتمل برای کاشی‌کاری فضایی با ابعاد بالا را نمایش می‌دهد؛ اما به‌سختی می‌توان چیزها را صرفا با یک معادله توضیح داد. گاهی برای توصیف مجموعه‌ای کاملا پیچیده در فضا، به چندین معادله نیاز دارید.

بنابراین، گرینفلد و تائو سعی کردند مسئله را اصلاح کنند. آن‌ها متوجه شدند که می‌توانند سیستمی از معادلات را طراحی کنند که در آن هر معادله، محدودیت متفاوتی را روی راه‌حل آن‌ها وضع می‌کند. به‌این‌ترتیب می‌توانند مسئله‌ی خود را به پرسشی درباره‌ی تعداد زیادی از موزاییک‌های مختلف تجزیه کنند. در این نمونه موزاییک‌ها می‌توانند یک فضای مشخص را با استفاده از مجموعه‌ی یکسانی از تبدیل‌ها بپوشانند.

برای مثال، در دو بعد می‌توانید صفحه را با لغزاندن مربعی به سمت بالا، پائین، چپ یا راست به‌اندازه‌ی یک واحد، بپوشانید؛ اما شکل‌های دیگر هم می‌توانند صفحه را با مجموعه‌ی دقیقی از جابه‌جایی‌ها بپوشانند: برای مثال مربعی دارای برآمدگی در لبه‌ی راست و حذف برآمدگی از لبه‌ی چپ مانند قطعه‌ای از پازل جیگساو عمل می‌کند.

اگر مربع را مانند یک قطعه پازل جیگساو در نظر بگیرید و دیگر موزاییک‌ها از مجموعه‌ی یکسانی از جابه‌جایی‌ها استفاده کنند، می‌توان آن‌ها را مانند برش‌های سرد ساندویچ انباشته کرد و موزاییکی ساخت که از یک مجموعه تبدیل برای پوشاندن فضای سه‌بعدی استفاده می‌کند. گرینفلد و تائو باید این کار را در ابعاد بیشتری انجام دهند. تائو می‌گوید، از آنجا که روی ابعاد بالاتری کار می‌کنیم، اضافه کردن یک بعد دیگر آسیب چندانی به کارمان نمی‌زند. به‌این‌ترتیب می‌توان به انعطاف بیشتری برای رسیدن به یک راه‌حل خوب دست یافت.

ریاضی‌دان‌ها می‌خواستند این روال ساندویچ‌سازی را معکوس کنند و معادله‌ی مسئله‌ی کاشی‌کاری در ابعاد بالا را به شکل مجموعه‌هایی از معادله‌های کاشی‌کاری در ابعاد پائین‌تر بازنویسی کنند. این معادله‌ها بعدا ساختار موزاییکی در ابعاد بالا را تعیین می‌کنند.

گرینفلد و تائو سیستم معادلات موزاییک‌کاری خود را به برنامه‌ای کامپیوتری تشبیه کردند: هر خط کد یا معادله یک دستور است و ترکیبی از دستورها می‌تواند به تولید برنامه‌ای بینجامد که به هدفی مشخص می‌رسد. به گفته‌ی تائو، مدارهای منطقی از گیت‌های AND و OR ساخته‌ شده‌اند که هر کدام به تنهایی جذابیتی ندارند؛ اما می‌توانید با انباشته‌سازی آن‌ها به مداری برسید که یک موج سینوسی ترسیم می‌کند یا ارتباطی اینترنتی را برقرار می‌کند.

بنابراین آن‌ها مسئله را به شکل نوعی مسئله‌ی برنامه‌نویسی در نظر گرفتند. هر کدام از دستورها هم‌ارز با ویژگی متفاوتی است که برای رسیدن به کاشی‌کاری نهایی ضروری است؛ بنابراین برنامه به‌صورت کلی تضمین می‌کند که کاشی‌کاری باید غیرتناوبی باشد.

سپس این پرسش مطرح شد که چه ویژگی‌هایی برای عملی کردن معادله‌های کاشی‌کاری لازم هستند. برای مثال موزاییکی در یک لایه از ساندویچ ممکن است به‌گونه‌ای شکل بگیرد که تنها اجازه‌ی انواع مشخصی از حرکت‌ها را بدهد. به همین دلیل ریاضی‌دان‌ها محدودیت‌های خود را به شکلی دقیق اعمال کردند تا مانع از تمام راه‌حل‌ها نشوند. به گفته‌ی گرینفلد، چالش اصلی در اینجا رسیدن به سطح مناسبی از محدودیت برای رمزنگاری معمای صحیح است.

معمایی که گرینفلد و تائو به دنبال برنامه‌نویسی آن با معادله‌های موزاییکی خود بودند، در واقع شبکه‌ای با تعداد نامتناهی سطر و تعداد زیادی اما متناهی، ستون بود. این دو ریاضی‌دان می‌خواستند هر سطر و هر قطر با توالی‌های مشخصی از اعداد پر شوند که هم‌ارز با انواع محدودیت‌هایی هستند که با معادله‌های کاشی‌کاری توصیف می‌شوند. آن‌ها این شبکه را به یک پازل عظیم سودوکو تشبیه کردند. این دو ریاضی‌دان سپس دریافتند که توالی‌ها غیرتناوبی بودند؛ به این معنی که راه‌حل سیستم مرتبط با معادله‌های موزاییکی هم غیرتناوبی بوده است. به گفته‌ی تائو، در اصل، تنها یک راه‌حل برای این معما وجود دارد و جالب است که «تقریبا» تناوبی است نه «کاملا».

همان‌طور که یوسویچ می‌گوید، گرینفلد و تائو در واقع یک شیء کاملا بنیادی را ایجاد کردند و آن را به موقعیتی رساندند که در آن همه چیز پیچیده‌تر به نظر می‌رسد. آن‌ها برای این کار یک موزاییک غیرتناوبی با ابعاد بالا را در ابتدا در یک تنظیمات گسسته و سپس در زمینه‌ای پیوسته ساختند. موزاییک آن‌ها به‌قدری پیچیده و پر از حفره است که به‌سختی فضا را می‌پوشاند. درواقع موزاییکی بی‌نظم است. تائو می‌گوید، هیچ تلاشی برای زیباسازی موزاییک نکرده است. او و گرینفلد بعدا فضای موزاییک را هم محاسبه نکردند، بلکه صرفا می‌دانند این فضا به بزرگی ۲ به توان ۱۰۰ به توان ۱۰۰ است. اگر سعی کنید این عدد را در صفحات تمام کتاب‌های جهان بنویسید باز هم کاغذ کم می‌آورید. اثبات آن‌ها نوعی اثبات ساختاری است، به گونه‌ای که همه‌چیز آشکار و قابل محاسبه باشد اما هنوز از حالت بهینه فاصله دارد.

در واقع، ریاضی‌دان‌ها تصور می‌کنند بتوانند موزاییک‌های غیرتناوبی را در ابعاد کمتر هم پیدا کنند. دلیل این ذهنیت این بود که برخی بخش‌های ساختار آن‌ها فضاهای خاصی را دربر می‌گرفتند که به فضای دوبعدی نزدیک بودند؛ اما گرینفلد معتقد بود که یک کاشی سه‌بعدی را پیدا کرده است و ممکن است یک کاشی چهاربعدی هم وجود داشته باشد.

پژوهش جدید بر راهی برای ساخت موزاییک‌های غیرتناوبی تأکید می‌کند که به باور گرینفلد و تائو می‌توان از آن برای نقض دیگر حدس‌های مرتبط با موزاییک استفاده کرد. به‌این‌ترتیب ریاضی‌دان‌ها می‌توانند مرزهای پیچیدگی این مسائل را جابه‌جا کنند. به گفته‌ی تائو به نظر می‌رسد هندسه‌ در ابعاد بالاتر بسیار کثیف و بی‌نظم باشد، به طوری که آسیب‌ها در این ابعاد خود را نشان می‌دهند و درکی که از دو یا سه بعد به دست می‌آوریم می‌تواند گمراه‌کننده باشد.

پژوهش جدید همچنین نه‌تنها مرزهای شهود انسان بلکه مرزهای استدلال ریاضی را زیر سؤال می‌برد. در دهه‌ی ۱۹۳۰ ریاضی‌دانی به نام کورت گودل نشان داد هر سیستم منطقی که برای توسعه‌ی محاسبات پایه کافی باشد، ناقص است. در واقع عبارت‌هایی وجود دارند که هرگز نمی‌توان آن‌ها را در چنین سیستمی اثبات یا نقض کرد. ریاضیات پر از عبارت‌های «تصمیم‌ناپذیر» است.

به طور مشابه ریاضیات پر از مسائل تصمیم‌ناپذیر از نظر محاسباتی است. مسائلی که نمی‌توان آن‌ها را با هیچ الگوریتمی در زمان متناهی حل کرد. ریاضی‌دان‌ها در دهه‌ی ۱۹۶۰ به این نتیجه رسیدند که مسائل مربوط به کاشی‌کاری هم تصمیم‌ناپذیر هستند. به‌طوری‌که برای برخی مجموعه شکل‌ها، محاسبه‌ی آن‌ها در زمان متناهی صرف‌نظر از کاشی‌کاری یک فضای مشخص، غیرممکن می‌شود. تنها راه حل این مسائل این است که تمام روش‌های محتمل برای قرار دادن کاشی‌ها را کنار یکدیگر درنظر بگیریم که ممکن است تا ابد به طول بینجامد.

گرینفلد و تائو سال گذشته به این نتیجه رسیدند که عبارت کلی زوج کاشی‌ها در ابعاد بالا، تصمیم‌ناپذیر است. آن‌ها ثابت کردند که هرگز نمی‌توان ثابت کرد زوج‌های مشخصی از کاشی‌ها می‌توانند به‌طور کامل فضایی را چه به شکل تناوبی چه غیرتناوبی، بپوشانند.

آیا عبارتی درباره‌ی یک کاشی واحد هم ممکن است تصمیم‌ناپذیر باشد؟ از دهه‌ی ۱۹۶۰ این فرض وجود دارد که اگر حدس کاشی‌کاری تناوبی صحیح باشد، می‌توان با هر نوع کاشی یک صفحه را پوشاند؛ اما عکس این مسئله لزوما صحیح نیست. تنها وجود یک کاشی غیرتناوبی به معنی وجود کاشی تصمیم‌ناپذیر نیست. این همان‌چیزی است که گرینفلد و تائو به دنبال حل آن هستند. تائو می‌گوید:

این فرض کاملا محتمل است. زبانی که ایجاد کردیم می‌تواند یک پازل تصمیم‌ناپذیر بسازد؛ بنابراین ممکن است کاشی‌هایی وجود داشته باشند که هرگز نتوانیم ثابت کنیم صفحه‌ای را می‌پوشانند یا نمی‌پوشانند.

ریاضی‌دان‌ها برای اثبات تصمیم‌ناپذیر بودن یک مسئله آن را با مسئله‌ی تصمیم‌ناپذیر دیگری مقایسه می‌کنند؛ بنابراین اگر مسئله‌ی کاشی‌کاری تصمیم‌ناپذیر باشد، می‌توان از آن به عنوان ابزاری برای اثبات تصمیم‌ناپذیری در مسائلی فراتر از کاشی‌کاری استفاده کرد.

در حال حاضر نتیجه‌ی گرینفلد و تائو مانند یک هشدار است. به گفته‌ی یوسویچ، ریاضی‌دان‌ها به دنبال عبارت‌های تمیز و زیبا هستند؛ اما هرچیزی را که می‌شنوید باور نکنید. متأسفانه تمام عبارت‌های جذاب ریاضی لزوما زیبا نیستند.