ریاضی‌دانان پس از ۳۲ سال جست‌وجو، نهمین عدد ددکیند را کشف کردند

به‌گزارش وب‌سایت ساینس آلرت، ریاضی‌دانان پس از گذشت نزدیک به سه دهه جست‌وجوی بی‌وقفه توانستند به‌کمک ابرکامپیوتر مثال جدیدی از عدد صحیح خاصی به نام عدد ددکیند را کشف کنند. این عدد نهمین نمونه از اعداد ددکیند یا D(9) نامیده می‌شود و برابر است با:

۲۸۶٬۳۸۶٬۵۷۷٬۶۶۸٬۲۹۸٬۴۱۱٬۱۲۸٬۴۶۹٬۱۵۱٬۶۶۷٬۵۹۸٬۴۹۸٬۸۱۲٬۳۶۶.

این رقم غول‌آسا پس از عدد قبلی ددکیند ۲۳ رقمی یا D(8) قرار دارد که در سال ۱۹۹۱ کشف شد. درک مفهوم عدد ددکیند برای افرادی غیر از ریاضی‌دانان دشوار است. در‌واقع، محاسبات مربوط به این عدد به‌قدری پیچیده و شامل رقم‌های بزرگ‌تر است که مشخص نبود پژوهشگران روزی بتوانند D(9) را کشف کنند. به‌گفته‌ی لنارت وان هیرتوم، دانشمند کامپیوتر دانشگاه پادربورن آلمان، به‌مدت ۳۲ سال محاسبه‌ی عدد D(9) مسئله‌ی بزرگی به‌شمار می‌رفت و حتی تصور می‌کردیم محاسبه‌ی این رقم غیرممکن باشد.

توابع بولی محور اصلی عدد ددکیند را تشکیل می‌دهند. این توابع منطقی معمولاً خروجی را از ورودی‌های دوحالتی مثل صحیح یا غلط (true یا false) یا صفر و یک انتخاب می‌کنند.

توابع بولی یکنوا توابعی هستند که عملگر منطقی را به جهتی خاص محدود می‌کنند؛ به‌گونه‌ای که جابه‌جایی صفر با یک در ورودی باعث تغییر خروجی از صفر به یک می‌شود، نه برعکس. پژوهشگران این مسئله را با استفاده از رنگ‌های سفید و قرمز به‌جای صفر و یک‌ها توصیف کردند؛ اما مسئله یکسان است.

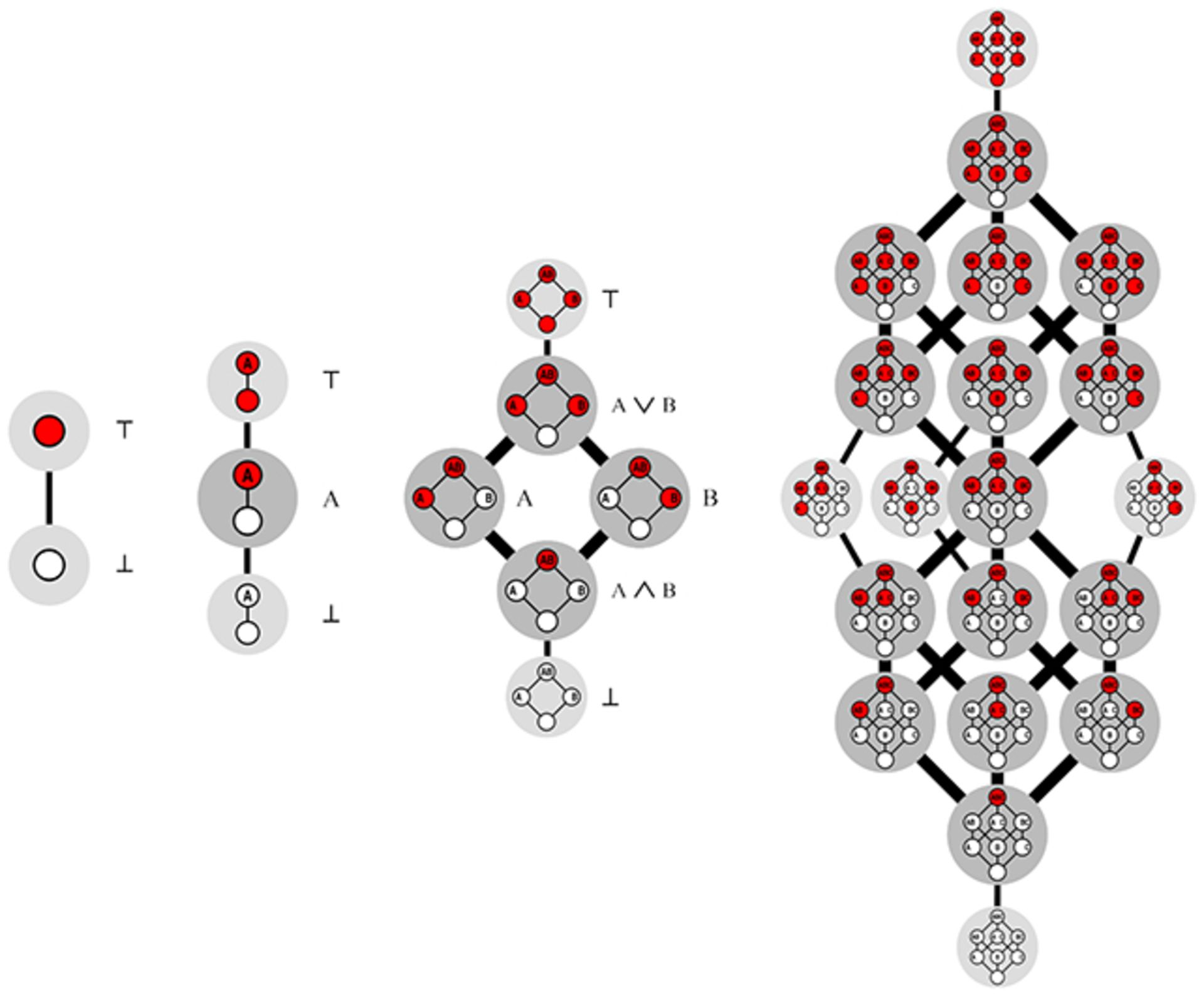
به‌گفته‌ی وان هیرتوم، می‌توان تابع بولی یکنوا را مانند یک بازی با مکعب n بعدی در دو و سه و بی‌نهایت بُعد در نظر گرفت. می‌توان مکعب را روی یک گوشه موازنه کرد و سپس رنگ هرکدام از گوشه‌های باقی‌مانده می‌تواند سفید یا قرمز باشد.

تنها یک قانون وجود دارد: هرگز نباید گوشه‌ی سفید را بالای گوشه‌ی قرمز قرار دهید. این کار باعث نوعی تقاطع قرمز-سفید عمودی می‌شود. هدف بازی،ژ شمارش تعداد بُرش‌های متفاوت است. رسیدن به چند عدد اول کار آسانی است. D(1) برابر است با ۲ و دیگر اعداد ددکیند عبارت‌اند از ۳، ۶، ۲۰، ۱۶۸ و به همین ترتیب ادامه می‌یابند.

داگ ویدمان ریاضی‌دان در سال ۱۹۹۱ با استفاده از ابرکامپیوتر Cray-2، یکی از ابرکامپیوترهای قدرتمند‌ آن زمان) به‌مدت ۲۰۰ ساعت عدد D(8) را محاسبه کرد.

طول ارقام D(9) تقریبا دو برابر طول D(8) است و به نوع خاصی از ابرکامپیوتر نیاز داشت؛ کامپیوتری که از واحدهای خاصی به نام آرایه‌های گیتی برنامه‌پذیر میدانی (FPGA) استفاده می‌کند و می‌تواند چند محاسبه را به‌صورت موازی انجام دهد. پژوهشگران برای محاسبه‌ی این عدد از ابرکامپیوتر Noctua 2 در دانشگاه پادربورن استفاده کردند.

به‌گفته‌ی کریستین پلسل، دانشمند کامپیوتر و سرپرست مرکز رایانش موازی (PC2)، محل نگه‌داری Noctua 2، حل مسائل ترکیبی با FPGA‌ها زمینه‌ی کاربردی امیدبخشی است و ابرکامپیوتر Noctua 2 از معدود ابرکامپیوترهای سراسر جهان است که می‌تواند چنین آزمایشی را انجام دهد.

بهینه‌سازی‌های بعدی برای کار با Noctua 2 لازم بودند. پژوهشگران با استفاده از تقارن‌های موجود در فرمول، جمعی بزرگ را برای محاسبه دراختیار ابرکامپیوتر قرار دادند که مجموعه‌ای شامل 5.5*10^18 عبارت بود. برای درک بهتر این تعداد بهتر است بدانید که تعداد دانه‌های شن روی زمین 7.5*10^18 تخمین زده شده است.

Noctua 2 پس از پنج ماه به پاسخ رسید و حالا ما D(9) را در‌اختیار داریم. پژوهشگران فعلاً اشاره‌ای به کشف D(10) نکرده‌اند؛ اما شاید کشف این عدد هم ۳۲ سال به‌طول بینجامد. هم‌اکنون، مقاله‌ای درباره‌ی این پژوهش منتشر نشده؛ اما قرار است در ماه سپتامبر در کارگاه بین‌المللی توابع بولی و کاربردهای آن‌ها (BFA) در نروژ ارائه شود.