شناسایی مسئله‌هایی که فقط با کامپیوترهای کوانتومی قابل حل هستند

پیش از این در دنیای مطالعات کامپیوترهای کوانتومی، دانشمندان علوم کامپیوتر یک پرسش اساسی را مطرح کردند؛ آن‌ها می‌دانستند که یافتن پاسخ این سؤال، به آشکار شدن ابعادی وسیع و ژرف درباره‌ی قدرت این ماشین‌ها می‌انجامد. اکنون ۲۵ سال از آن زمان سپری شده است و به‌نظر می‌رسد بسیاری از پرسش‌هایی که شاید در آن زمان دشوار یا بی‌پاسخ می‌کردند، هم‌اکنون حل‌وفصل شده‌اند. دو دانشمند کامپیوتر با نام‌های ران راز و اویشای تال در مقاله‌ای که به‌صورت آنلاین در پایان ماه مه (خرداد) منتشر شد، شواهد قوی ارائه داده‌اند مبنی بر اینکه کامپیوترهای کوانتومی دارای ظرفیت محاسباتی بسیار فراوانی هستند؛ بسیار بیشتر از هر نوع طرفیتی که تاکنون در دنیای کامپیوترهای کلاسیک به دست آمده‌ است.

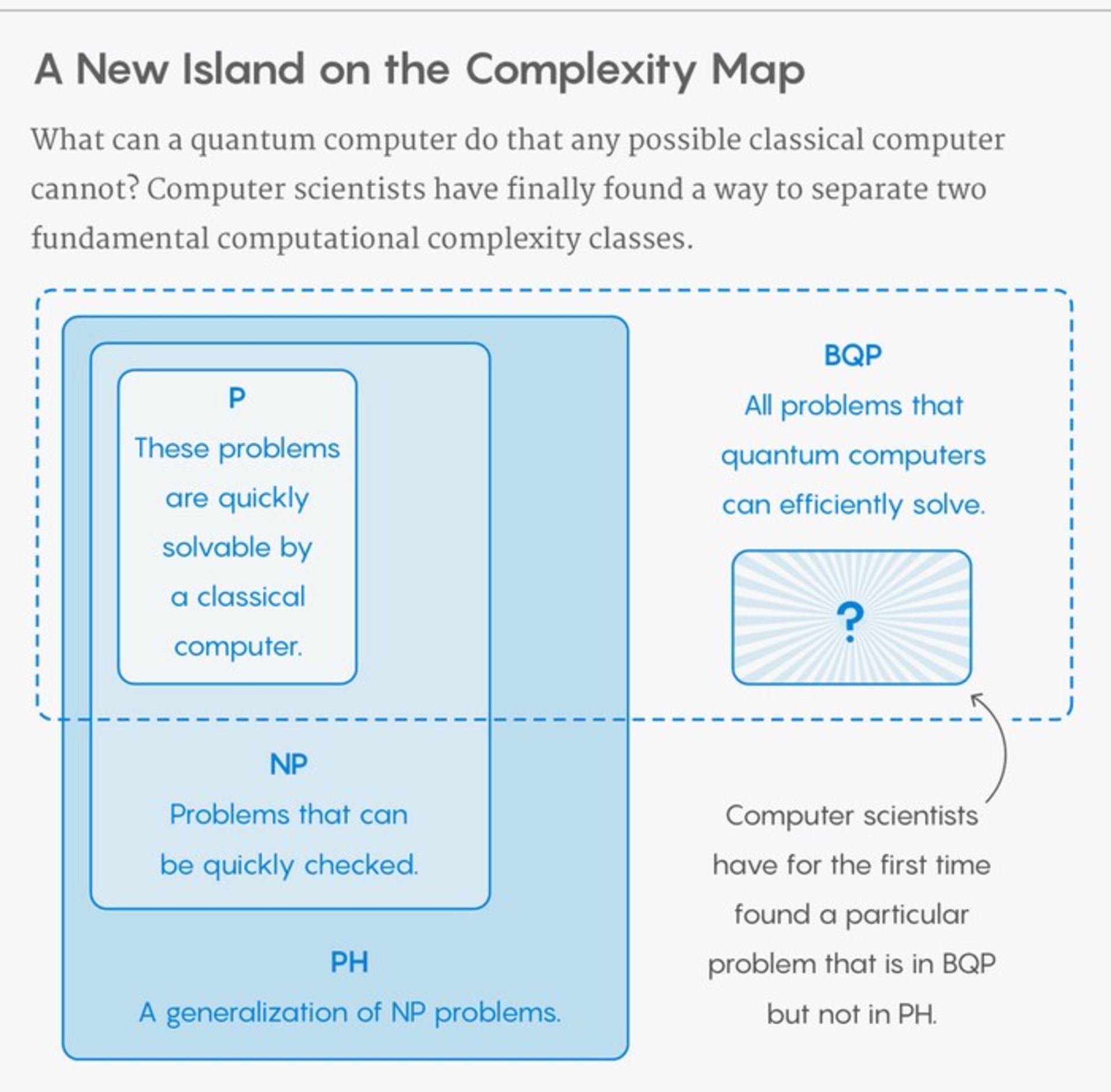
راز، استاد فعال در دانشگاه پرینستون و مؤسسه‌ی علمی وایزمن به همراه تال، یکی از اعضای فعال در دوره‌ی پسادکترا در دانشگاه استنفورد، نوع خاصی از مسئله‌ی محاسباتی را تعریف می‌کنند. آن‌ها با در نظر گرفتن یک پیش‌فرض خاص، ثابت می‌کنند که کامپیوترهای کوانتومی می‌توانند مسئله‌ی مورد نظر را به‌صورت مؤثر مدیریت کنند. این در حالی است که کامپیوترهای کلاسیک تا ابد نیز از پس حل آن بر نخواهند آمد. دانشمندان علوم کامپیوتر از سال ۱۹۹۳ به‌دنبال حل چنین مسئله‌ای بوده‌اند. آن‌ها در آن زمان، برای اولین بار دسته‌ای از مسائل شناخته‌شده به نام BQP را تعریف کردند. این دسته شامل همه‌ی مسائلی است که کامپیوترهای کوانتومی توانایی حل آن‌ها را دارند.

از آن زمان به بعد، دانشمندان کامپیوتر همواره امیدوار بوده‌اند که بتوانند BQP را با یک دسته از مسائل شناخته‌شده با عنوان PH متمایز کنند. PH شامل تمام مسائلی می‌شود که هر کامپیوتر کلاسیک امروزی و حتی کامپیوترهای کلاسیکی که در زمان‌های آینده و توسط نسل‌های آینده ساخته خواهد شد، توانایی کار روی آن‌ها را دارد. ایجاد این تمایز یا تقابل بین دو دسته‌ی یادشده، به یافتن نوعی از مسائل بستگی دارد که بتوانند در دسته‌ی BQP جای بگیرند؛ اما جزو دسته‌ی PH هم نباشند. اکنون و پس از سال‌ها، راز و تال همین کار را انجام داده و چنین مسئله‌ای را تعریف کرده‌اند.

وظیفه اصلی علوم کامپیوتر تئوری این است که مسائل را به کلاس‌ها یا رده‌های پیچیده تقسیم کند. رده‌ی پیچیدگی دربردارنده‌ی تمام مسئله‌هایی است که می‌تواند در یک بودجه منابع مشخص و تخصیص‌یافته حل شود. در اینجا منظور از منابع، می‌تواند زمان یا مقدار حافظه باشد.

دانشمندان کامپیوتر یک الگوریتم کارآمد شناسایی کرده‌اند. به‌عنوان مثال، الگوریتمی برای تعیین اینکه کدام عدد اول است. با این حال، آن‌ها نتوانسته‌اند الگوریتمی کارآمد برای شناسایی عوامل اول اعداد بزرگ پیدا کنند. از همین رو، دانشمندان کامپیوتر بر این باورند (اما پیش از این نمی‌توانستند اثبات کنند) که دو مسئله‌ی فوق، متعلق به کلاس‌های پیچیدگی متفاوتی هستند.

دو مورد از معروف‌ترین کلاس‌های پیچیدگی با عناوین P و NP شناخته شده‌اند. P مربوط به همه‌ی مسئله‌هایی است که یک کامپیوتر کلاسیک می‌تواند به‌سرعت حل کند. پرسش مربوط به اول بودن یا نبودن یک عدد، در همین کلاس پیچیدگی P قرار می‌گیرد. کلاس NP هم مربوط به تمام مسائلی است که کامپیوترهای کلاسیک نمی‌توانند آن‌ها را لزوما به‌سرعت حل کنند؛ اما اگر یک جواب برایشان ارائه شود، می‌توانند درستی یا نادرستی آن را بسیار سریع تعیین کنند. دانشمندان کامپیوتر معتقدند که P و NP کلاس‌های متمایز هستند؛ اما در واقع ثابت کردن همین تمایز از نظر علمی، سخت‌ترین و مهم‌ترین مسئله‌ای در این رشته است که بایستی به آن پاسخ داده شود.

دانشمندان کامپیوتر با نام‌های اتان برنشتاین و اوسمش وزیرانی در سال ۱۹۹۳، کلاس جدیدی از پیچیدگی را تعریف کردند و نام BQP را برای آن در نظر گرفتند که مخفف‌شده‌ی عبارت چندجمله‌ای کوانتومی با خطای محدود بود. آن‌ها BQP را به‌عنوان طبقه‌ای تعریف کردند که حاوی تمامی مسئله‌های مربوط به تصمیم‌گیری باشد؛ مسئله‌های تصمیم‌گیری به مسئله‌هایی با یک جواب بله یا خیر اطلاق می‌شود و کامپیوترهای کوانتومی می‌توانند برای حل آن‌ها کارآمد باشند. تقریبا در همان زمان نیز ثابت شد که کامپیوترهای کوانتومی می‌توانند تمام مسائل قابل حل توسط کامپیوترهای کلاسیک را حل کنند. یعنی، BQP شامل تمام مسئله‌های موجود در دسته‌ی P است.

اما آن‌ها نمی‌توانستند تعیین کنند که آیا BQP دارای مسائلی است که در یکی دیگر از کلاس‌های مهم شناخته‌شده به‌عنوان PH وجود نداشته باشد؟ PH مخفف‌شده‌ی عبارت سلسله مراتب چندجمله‌ای است. PH در واقع تعمیمی از NP است. یعنی اینکه این دسته شامل تمام مسائلی است که شما با آغاز یک مسئله در دسته NP و پیچیده‌تر ساختن آن با افزودن حالت‌های کیفی همچون سور وجودی یا عمومی به‌دست خواهید آورد. امروزه کامپیوترهای کلاسیک نمی‌توانند بخش عمده‌ای از مسئله‌های PH را حل کنند؛ اما شما می‌توانید PH‌ را به‌عنوان کلاسی برای تمام آن مسائل کامپیوتری در نظر بگیرید که درصورت  برابر شدن P با NP، می‌توانند حل شوند. به‌عبارت دیگر، مقایسه‌ی BQP و PH، به‌منزله‌ی تعیین این موضوع است که آیا کامپیوترهای کوانتومی مزیت و کارامدی بیشتری نسبت به کامپیوترهای کلاسیک دارند؟ حتی اگر کامپیوترهای کلاسیک بتوانند به‌طور غیرمنتظره‌ای به جایی برسند که مسائل بسیار بیشتری را در قیاس با امروز حل کنند.

اسکات آرونسون، دانشمند علوم کامپیوتر در دانشگاه تگزاس در آستین، گفت:

PH یکی از اساسی‌ترین کلاس‌های پیچیدگی کلاسیکی است که وجود دارد. از همین رو ما می‌خواهیم بدانیم که جایگاه محاسبات کوانتومی در دنیای تئوری پیچیدگی‌های کلاسیک دقیقا کجا خواهد بود.

بهترین روش برای تشخیص بین دو کلاس پیچیدگی، یافتن مسئله‌ی است که به‌طرز قابل اثباتی در یک کلاس باشد و در دیگری نه. با این حال، با توجه به وجود ترکیبی از موانع اساسی و فنی، یافتن چنین مسئله‌ای برای دانشمندان به یک چالش جدی تبدیل شده است. آرونسون گفت:

اگر به‌دنبال مسئله‌ای باشید که در کلاس BQP باشد و در PH جای نگیرد؛ باید حالتی را مشخص کنید که یک کامپیوتر کلاسیک با تعاریف موجود از آن، حتی نتواند درستی نا نادرستی جواب آن را تعیین کند؛ چه رسد به اینکه قادر به حل آن مسئله باشد. همین شرط باعث می‌شود بسیاری از مسائلی که ما در دنیای علوم کامپیوتر در نظر می‌گیریم، از درجه‌ی کارامدی برای این چالش ساقط شوند.

در اینجا یک مسئله را مرور می‌کنیم. تصور کنید که دو تولیدکننده‌ی عدد تصادفی در اختیار دارید و هر کدام از آن‌ها دنباله‌ای از ارقام را تولید می‌کنند. پرسش مطرح‌شده برای کامپیوتر شما این است: آیا دو دنباله کاملا مستقل از یکدیگر هستند؟ یا آن‌ها به روش پنهان (جایی که یک دنباله، تبدیل فوریه‌ای از دنباله‌ی دیگر است) عمل می‌کنند؟ آرونسون این مسئله‌ی مرتبط با ارتباط یا forrelation را در سال ۲۰۰۹ معرفی کرد و ثابت کرد که این مسئله متعلق به کلاس BQP است. پس از آن ما با یک مرحله‌ی ثانویه و بسیار دشوارتر رو‌به‌رو شدیم: باید اثبات می‌کردیم که مسئله‌ی ارتباط در دسته‌ی PH هم قرار ندارد.

این همان کاری است که راز و تال انجام داده‌اند. مقاله‌ی آن‌ها، به یک تمایز یا جدایی میان BQP و PH رسیده است؛ موردی که با نام جدایی اوراکل یا جعبه‌ی سیاه می‌شناسیم. این یک نتیجه از نوع متداول در علوم کامپیوتر است؛ و در عین حال یکی از آن نتایجی که پژوهشگران درصورت نیاز به اثبات موارد خارج از دسترس خود، به آن متوسل می‌شوند.

بهترین راه واقعی برای تشخیص کلاس‌های پیچیدگی مانند BQP و PH این است که زمان محاسباتی مورد نیاز برای حل یک مسئله را در هر یک از آن‌ها اندازه‌گیری کنیم. هنری یون، دانشمند کامپیوتر در دانشگاه تورنتو می‌گوید:

اما دانشمندان کامپیوتر هیچ درک پیچیده‌ یا همچنین هیچ توانایی کاملی برای اندازه‌گیری زمان واقعی محاسبه ندارند.

از همین رو، دانشمندان کامپیوتر مورد دیگری را می‌سنجند و امیدوار هستند که اندازه‌گیری آن‌ها بتواند دیدگاهی را درمورد زمان محاسبه‌ای که نمی‌توانند اندازه گیری کنند، پیش رویشان بگذارد. آن‌ها تعداد دفعات رجوع به اوراکلی را که یک کامپیوتر نیاز دارد تا به یک مسئله جواب دهد، شمارش می‌کنند. یک اوراکل مانند یک اشاره‌گر است. شما نمی‌دانید که جهت‌ها و اشاره‌ها به چه شکلی به دست می‌آید؛ اما می‌دانید که قابل اعتماد هستند.

اگر مسئله‌ی مورد نظر این باشد که آیا دو تولیدکننده‌ی عدد تصادفی به‌طور مخفیانه با یکدیگر مرتبط هستند یا خیر، می‌توانیم از اوراکل پرسش‌هایی از این دست بپرسیم: عدد ششم از هر تولیدکننده چیست؟ در ادامه بایستی قدرت محاسباتی را بر مبنای تعداد اشاره‌های مورد نیاز هر نوع کامپیوتری برای حل مسئله مقایسه کنیم. برای حل مشکل. کامپیوتری که نیاز به اشاره‌ها یا علائم بیشتری دارد، کندتر است. تال می‌گوید:

به‌تعبیری، ما این مدل را بسیار بهتر درک می‌کنیم. این حالت بیشتر از اینکه در‌مورد اطلاعات باشد، پیرامون محاسبات است.

مقاله‌ی جدید راز و تال نشان می‌دهد که یک کامپیوتر کوانتومی در قیاس با یک کامپیوتر کلاسیک، نیاز به اشاره‌های کمتری برای حل مسئله‌ی ارتباط دارد. درواقع، یک کامپیوتر کوانتومی فقط نیاز به یک اشاره دارد. این در حالی است که حتی با وجود اشاره‌ها یا راهنمایی‌های نامحدود نیز هیچ الگوریتمی در PH وجود ندارد که بتواند همان مسئله را حل کند. به‌گفته‌ی راز:

این بدان معنا است که یک الگوریتم کوانتومی بسیار کارآمد برای حل این مسئله وجود دارد؛ اما اگر شما فقط الگوریتم‌های کلاسیک را در نظر بگیرید، حتی اگر به کلاس‌های بسیار بالایی از الگوریتم‌های کلاسیک هم رجوع کنید، از پس حل مسئله بر نخواهند آمد.

همین روند تأیید می‌کند که در یک اوراکل، ارتباط به‌عنوان مسئله‌ای در نظر گرفته می‌شوند که در کلاس ‌BQP قرار دارد؛ اما در PH نه.

راز و تال این نتیجه را تقریبا چهار سال پیش به‌دست آوردند؛ اما نمی‌توانستند آن گام کلیدی درمورد اثبات موضوع را به اتمام برسانند. اکنون پس از گذشت چهار سال و در حدود یک ماه پیش، تال متوجه مقاله‌ای پیرامون تولیدکننده‌های اعداد تصادفی کاذب شد و دریافت که روش‌های مطرح‌شده در آن مقاله، درست همان‌هایی بودند که او و راز برای اتمام روش‌های خودشان نیاز دارند. وی از این یافته با تعبیر تکه‌ی گمشده‌ی پازل یاد می‌کند.

کار پژوهشی اخیر هیچ جای شک و تردیدی در این واقعیت باقی نمی‌گذارد که کامپیوترهای کوانتومی در قلمروی محاسباتی کاملا متفاوتی از کامپیوترهای کلاسیک (حداقل نسبت به اوراکل) قرار دارند. حتی اگر تصور کنیم زمانی در جهان ما، P برابر NP تلقی شود، که این به خودی خود فرض دور از ذهن و عجیبی است و در آن حالت، مسئله‌ی فروشنده‌ی دوره‌گرد به‌سادگی یافتن پاسخ یک برون‌یابی ساده خواهد بود، باز هم مسائلی وجود خواهند داشت که تنها با کامپیوترهای کوانتومی قابل حل باشند.  لانس فورتنو دانشمند علوم کامپیوتر در این مورد گفته است:

حتی اگر P برابر با NP باشد و ما این فرض دشوار را هم در نظر بگیریم، باز هم برای غلبه بر توانایی محاسبات کوانتومی ناکافی خواهد بود.