۱۲ مورد از بحث برانگیزترین معماهای ریاضی (قسمت اول)

 حتماً تا به حال برایتان پیش آمده است که یکی از دوستان علاقه‌مند به ریاضیات، برایتان معمایی مطرح کرده باشد؛ از آن نوع معماهایی که به گونه‌ای طراحی شده‌اند تا ذهن را به سمت جوابی آسان و غلط منحرف کنند. احتمالاً پس از اینکه جواب غلط مورد نظر دوست‌تان را داده‌اید، او با لبخندی پیروزمندانه برایتان توضیح داده است که کجای کار دچار اشتباه شده‌اید.

اگر می‌خواهید شما هم در چنین مواقعی در جمع دوستان چند معما در آستین داشته باشید، در ادامه با چند مورد از بحث برانگیزترین و غیر قابل قبول‌ترین آن‌ها آشنا خواهید شد. توضیح علت درست بودن بعضی از حقایقی که در ادامه به آن‌ها اشاره خواهد شد، کار چندان آسانی نیست و به احتمال زیاد خیلی‌ها حاضر به قبول کردن صحت آن‌ها نخواهند شد.

علاوه بر معماها، به چند مورد از قوانین و پارادوکس‌های عجیب دنیای ریاضیات نیز اشاره خواهیم کرد.

فرض کنید در یک مسابقه‌ی تلویزیونی، مجری برنامه ۳ در به شما نشان می‌دهد که پشت یکی از آن‌ها یک ماشین آخرین مدل قرار گرفته است؛ درحالی‌که پشت دو در دیگر دو بز قرار دارند. به شما فرصت انتخاب یک در داده می‌شود. پس از اینکه یکی از درها را انتخاب کردید، مجری یکی از دو دری که انتخاب نکرده بودید را باز می‌کند تا چشمان‌تان به جمال یکی از بزها روشن شود.

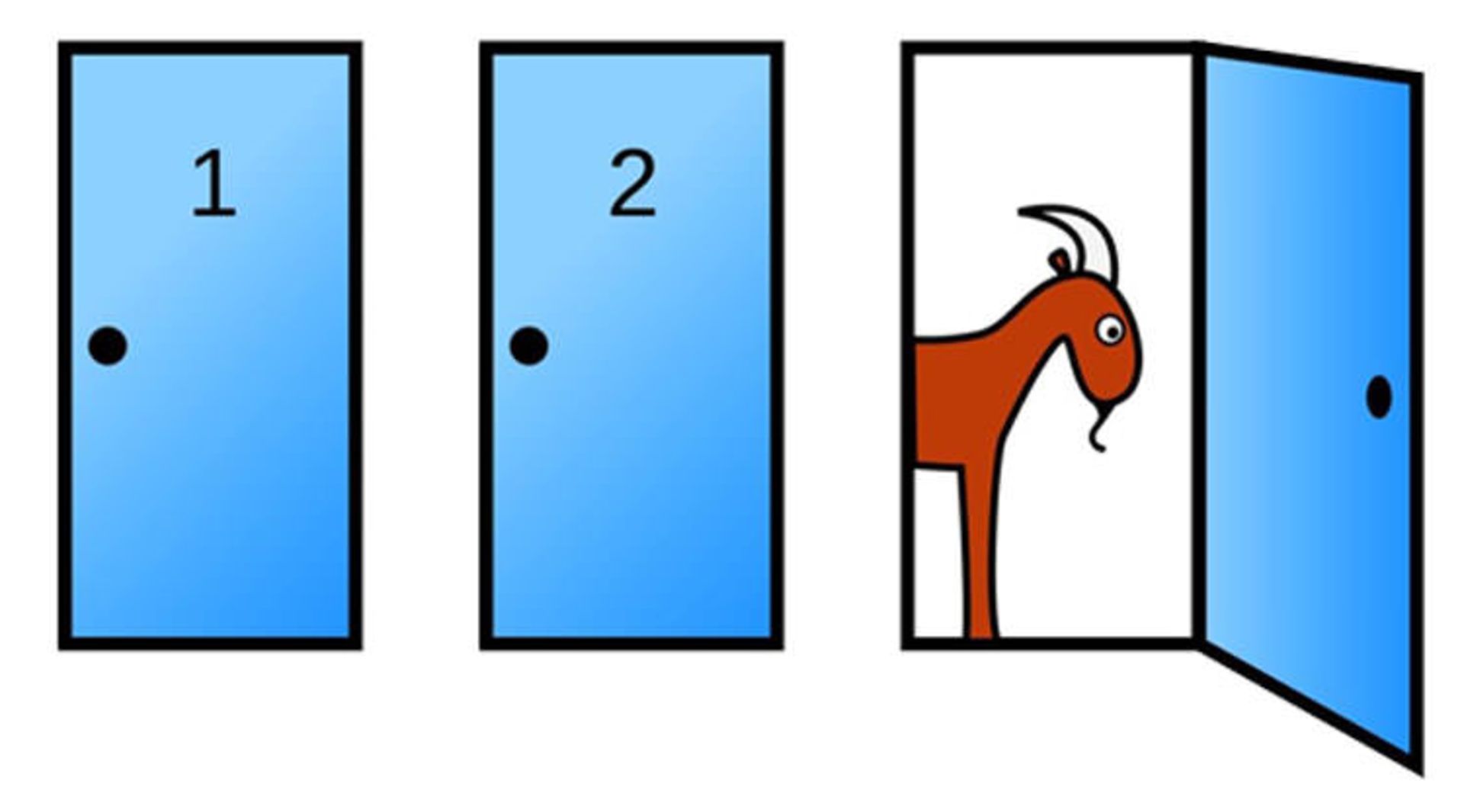
سپس مجری از شما می‌پرسد که آیا می‌خواهید در انتخابی‌ خود را عوض کنید، یا همان در قبلی را نگه خواهید داشت؟

شما باشید چه می‌کنید؟ اگر فکر می‌کنید که چون تنها دو در باقی مانده، شانس شما ۵۰-۵۰ است، اشتباه می‌کنید!

اما چطور ممکن است که با وجود تنها دو گزینه برای انتخاب، شانس برد و باخت شما با هم برابر نباشند؟ 

• شرکت‌ کننده‌ای که در انتخابی خود را عوض کند، تنها در صورتی می‌بازد که پشت در انتخابی‌اش ماشین بوده باشد.
• از آنجایی که شانس ماشین بودن پشت در در انتخاب اول یک سوم است، پس شانس باخت در صورت تعویض در هم یک سوم است.
• یعنی کسی که در انتخابی‌اش را عوض کند دو سوم شانس پیروزی دارد و این دوبرابر شانس کسی است که تصمیم به عدم تعویض در گرفته است.

هنوز هم قانع نشده‌اید؟

فرض کنید در شماره‌ی ۱ را انتخاب کرده‌اید. جدول زیر تمام حالات ممکن را نشان می‌دهد:

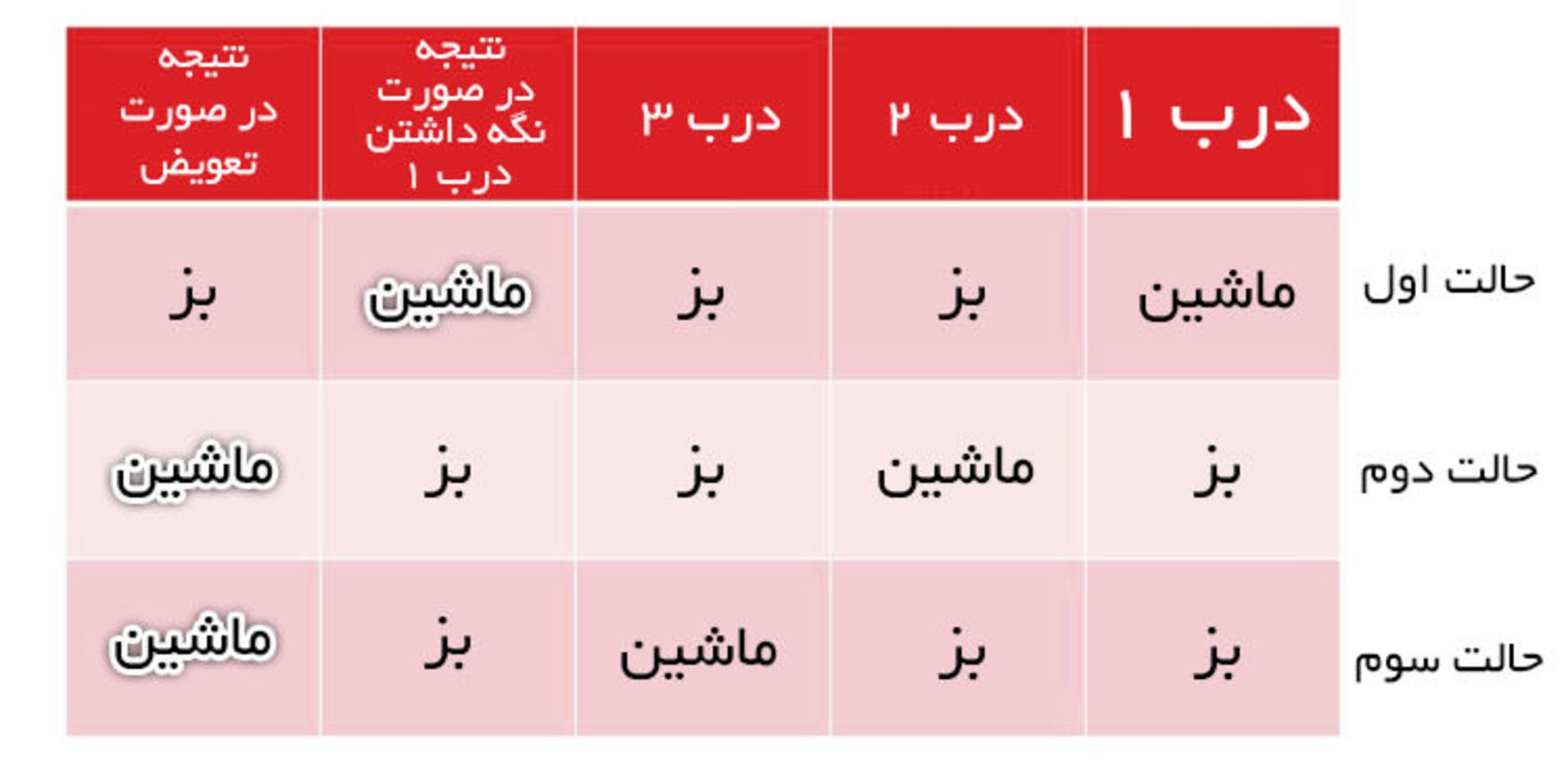
اگر در انتخابی خود را عوض نکنید، از هر سه بار، تنها یک بار برنده می‌شوید، درحالی‌که در صورت تعویض، دو بار در هر سه بار برنده خواهید شد.

اگر هنوز هم قانع نشده‌اید، همین مسئله را این بار با ۵۰ در در نظر بگیرید. در اول را انتخاب می‌کنید و مجری با باز کردن ۴۸ در، ۴۸ بز زیبا به شما نشان می‌دهد.

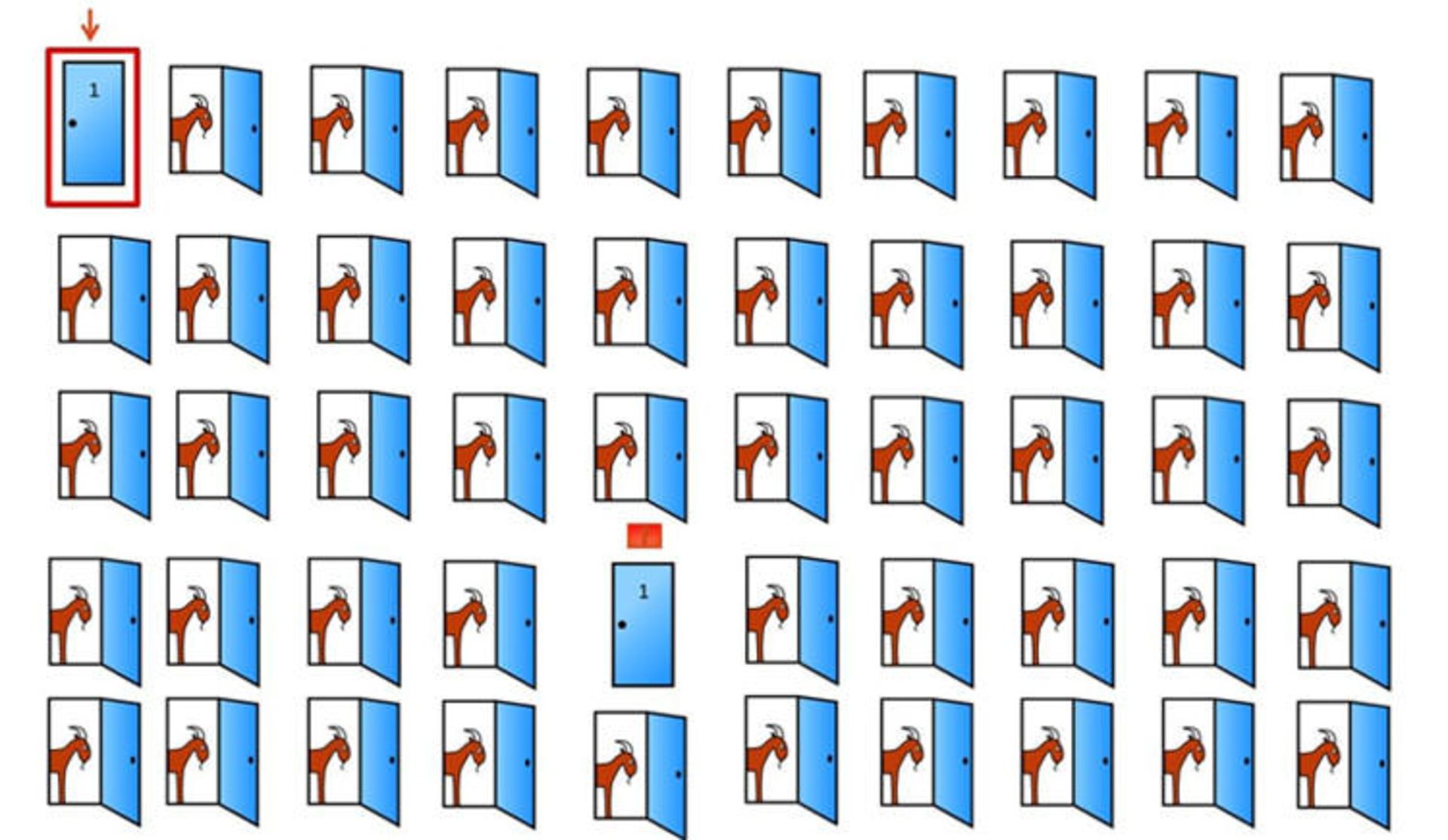
هنوز هم به انتخاب اول‌تان مطمئن هستید؟ به یاد داشته باشید که در انتخاب اول شانس شما ۱ در ۵۰ بود و این مثال هم بر مبنای همان قواعد مثال قبل است. البته تمامی این استدلال‌ها با فرض این است که قصد انتخاب ماشین را داشته باشید، نه بز!

اگر فکر می‌کنید که در تساوی بالا ... ۰/۹۹۹ دقیقاً برابر با عدد ۱ نیست و بنابراین باید به‌جای علامت تساوی از علامت کوچکتر (>) استفاده شود، کاملاً در اشتباه هستید. روش‌های مختلفی برای اثبات این حقیقت وجود دارند، اما خیلی‌ها همچنان حاضر به قبول کردن آن نمی‌شوند. برای مثال یکی از این اثبات‌ها در زیر آورده شده است:

x = 0.999...

10x = 9.999...

10x - x = 9.999... - 0.999...

9x = 9

x = 1

یکی از دلایلی که خیلی‌ها در فهم این حقیقت ریاضی مشکل دارند، نداشتن درک درست از مفهوم «بی نهایت» است. اکثر افراد تصور می‌کنند بالاخره یک ۹ نهایی در انتهای لیست اعداد پس از اعشار وجود دارد.

اعداد را می‌توان به شکل‌های متفاوتی نوشت و ... ۰/۹۹۹ در واقع شکل دیگری از عدد ۱ است. اثبات اینکه این دو عدد با هم برابر هستند رابطه‌ی تنگاتنگی با مفهوم «حد» و «بی نهایت» در ریاضیات دارد.در زیر اثبات دیگر برای مسئله‌ی بالا آورده شده است:

⅓ = 0.333…

3 * ⅓ = 3 * 0.333…

1 = 0.999…

اعداد طبیعی (Natural Numbers)، اعدادی هستند که با آن‌ها می‌شماریم. (۱، ۲، ۳، ۴، ۵، ...)

بی‌نهایت عدد طبیعی، و همچنین بی‌نهایت عدد زوج وجود دارد. شاید تصور کنید که اعداد طبیعی از لحاظ تعداد از اعداد زوج بیشتر هستند، چرا که اعداد طبیعی خود از اعداد زوج به اضافه‌ی اعداد فرد تشکیل شده‌اند؛ اما این استدلال غلط است.

می‌توان یک تناظر یک به یک بین اعداد طبیعی و اعداد زوج برقرار کرد. این تابع دوسویی نشان می‌دهد که به ازای هر عدد طبیعی یک عدد زوج وجود دارد.

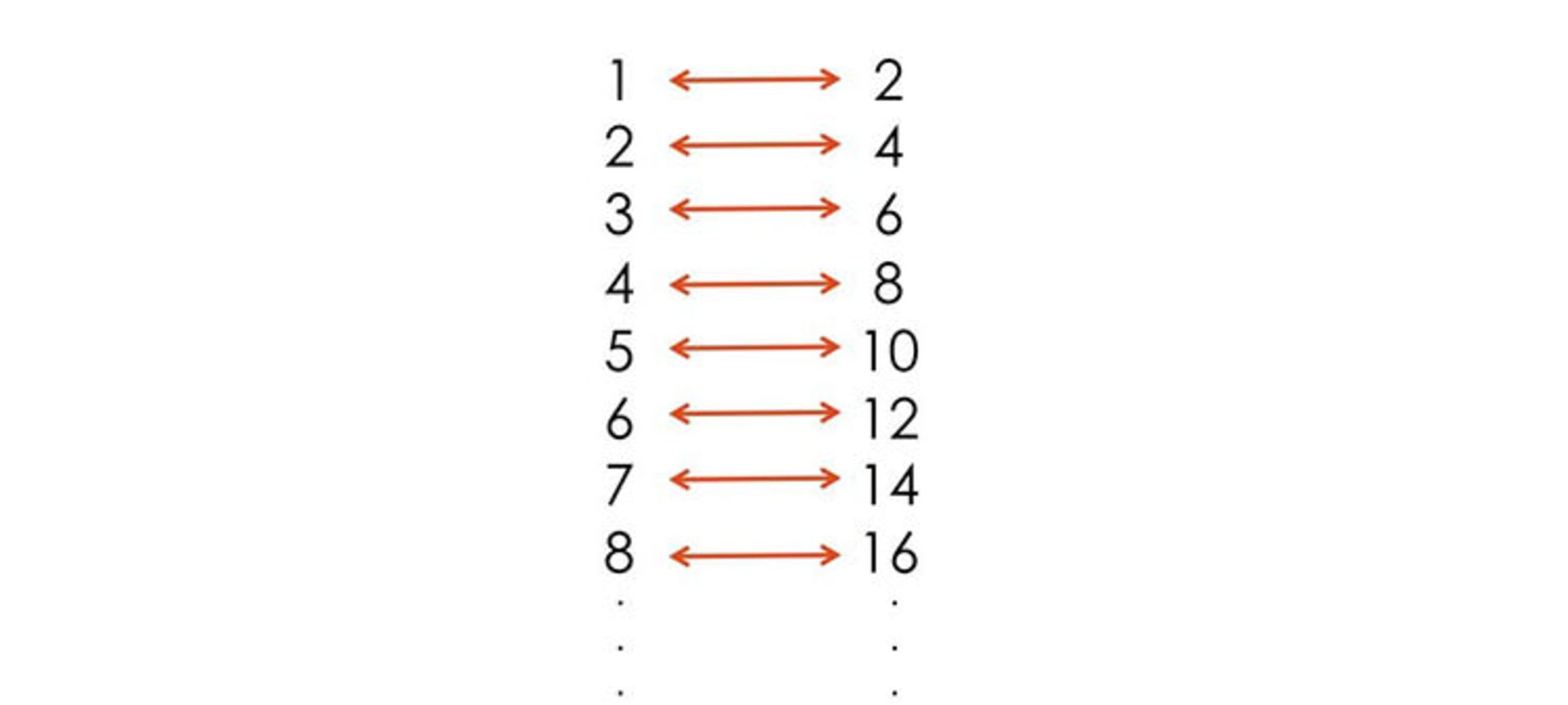
برای درک بهتر این موضوع، این حقیقت را در نظر بگیرید که به ازای هر عدد طبیعی، عددی وجود دارد که دو برابر آن است. همچنین به ازای هر عدد زوج، عددی وجود دارد که نصف آن است. این یعنی هر دو مجموعه‌ی نامتناهی مورد نظر از لحاظ تعداد اعضا با هم برابر هستند. دلیل این برابر بودن هم «قابل شمارش بودن» این دو مجموعه‌ی نامتناهی است.

برای مثال، نمی‌توانید یک تناظر یک به یک بین مجموعه‌ی اعداد طبیعی و مجموعه‌ی اعداد حقیقی برقرار کنید، چرا که دومی یک مجموعه‌ی نامتناهی «غیر قابل شمارش» است.

در ۳۰ درصد مواقع، رقم اول اعدادی که در دنیای واقعی با آن‌ها رو‌به‌رو می‌شویم «۱» است.

این موضوع اولین‌بار توسط فرانک بنفورد فیزیک‌دان، در سال ۱۹۳۸ کشف شد. میزان ظاهر شدن سایر اعداد در رقم اول نیز توزیع لگاریتمی به شکل زیر دارد.

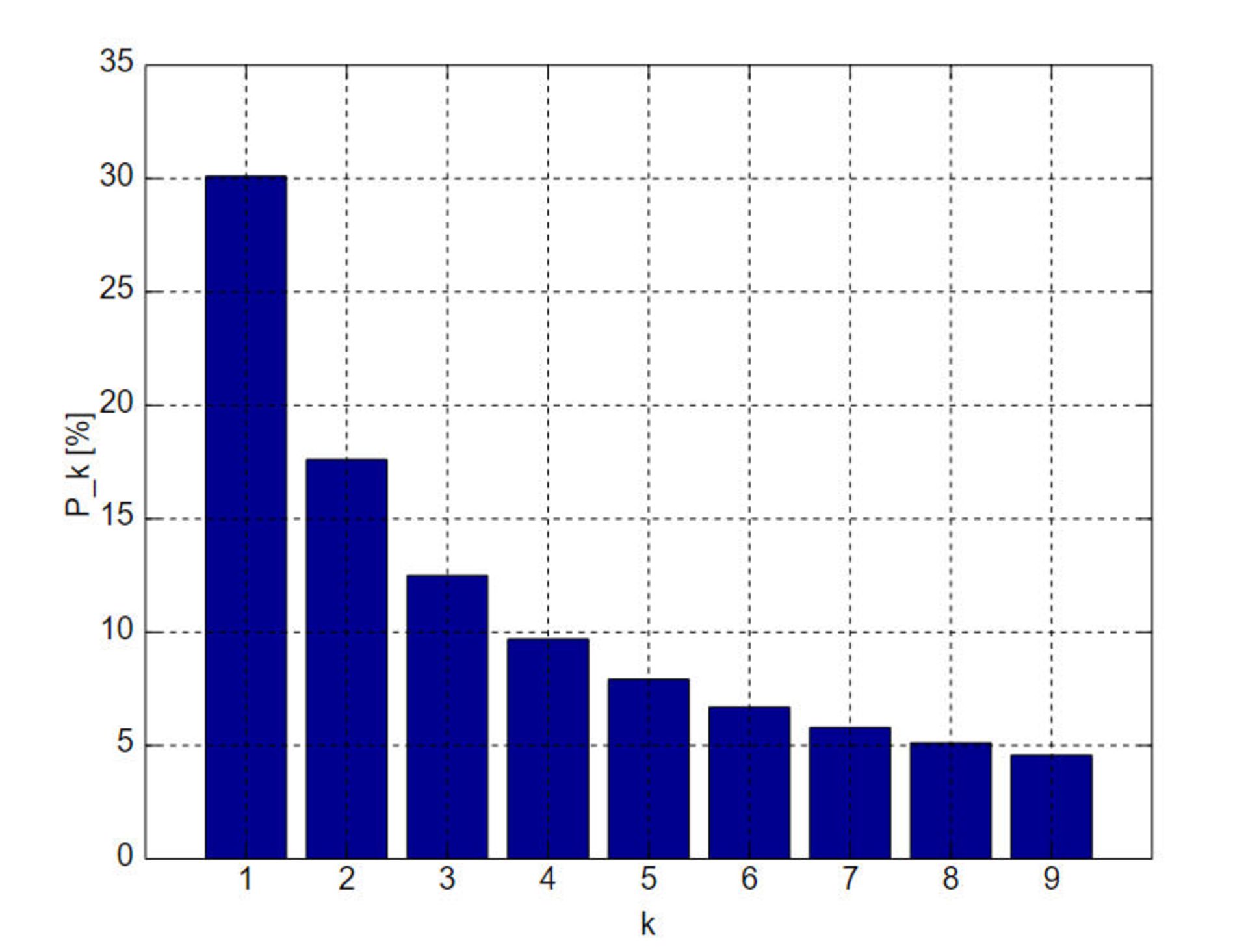
با وجود اینکه این قانون تجربی به‌صورت شهودی در اکثر مواقع صدق می‌کند، مدت‌ها پس از کشف همچنان توضیح و اثبات علمی دقیقی برای آن وجود نداشت؛ تا اینکه ریاضی‌دانی با نام تئودور هیل در سال ۱۹۹۶ توانست آن را اثبات کند.

از این قانون برای تشخیص داده‌های ساختگی از داده‌های واقعی در مواردی مانند تعداد رأی‌ها در انتخابات، آمار اقتصادی کاذب و اطلاعات حسابداری جعلی استفاده می‌شود.

این قانون همچنین در مجموعه اعداد فیبوناچی، فاکتوریل‌ها و مجموعه‌ی توان‌های عدد ۲ نیز به چشم می‌خورد.

این مقاله ادامه دارد...