لوح ۳۷۰۰ ساله، قدیمی ترین نمونه هندسه کاربردی

این لوح ارزشمند که Si.427 نامگذاری شده، برای بیش از صد سال در موزهای در استانبول نگهداری میشده است.
به گفته دنیل منسفیلد، ریاضیدان دانشگاه نیوساوت ولز استرالیا، Si.427 متعلق به دوره بابل کهن (۱۹۰۰ تا ۱۶۰۰ پیش از میلاد) است.
این تنها سند مرزبندی یافت شده از دوره بابل کهن است؛ که به عنوان یک نقشه برای تعیین مرز زمینها توسط نقشهبرداران استفاده میشده. در این خشت، اطلاعات قانونی و هندسی یک قطعه زمین، پس از تقسیم و فروش بخشی از آن ثبت شده است.
این نقشه از دستههایی از اعداد به نام سهتاییهای فیثاغورثی، برای بدست آوردن دقیق زوایای قائمه یا یافتن دستههایی از اعداد منطبق بر مدلهای مثلثاتی برای محاسبه اضلاع یک مثلث قائمالزاویه، استفاده میکند. استفاده از این روشها، تعیین سن این دستساخته را بهویژه بهدلیل پیامدهایی که در تاریخ ریاضیات دارد، با اهمیت میکند.
منسفیلد و همکارانش این اکتشاف را در مقاله جدیدی منتشر کردهاند و به تحلیل محتویات این لوح در کنار یافتههای جدیدی از لوحی همقدمت با Si.427 که با نام پلیمپتُن۳۲۲ (Plimpton 322) شناخته میشود، پرداختهاند. در سال ۲۰۱۷ مشخص شد که پلیمپتن۳۲۲ در واقع یک جدول مثلثاتی ابتدایی، شامل فهرستی از سهتاییهای فیثاغورسی است.

لوح پلیمپتن۳۲۲
در زمان این کشف، پژوهشگران کاربرد این جدول را نمیدانستند؛ اما اکنون گمان میکنند پلیمپتن۳۲۲ ممکن است کمی بعد از Si.427 ساخته شده و فقط حاوی سهتاییهای فیثاغورسی مورد نیاز برای اندازهگیری زمینهای مستطیل شکل باشد. به عبارت دیگر، پلیمپتن۳۲۲ یک راهنمای نقشهبرداری بوده است.
این شیوه استفاده از مثلثات، متمایز از روشی است که فیثاغورس، در سده دوم پیش از میلاد با نگاه به ستارگان ابداع کرد. تعداد سهتاییهای فیثاغورسی که نقشهبرداران بابلی میتوانستند استفاده کنند، بسیار محدود بود.
یک سهتایی فیثاغورسی باید در معادله a۲+b۲=c۲ صدق کند. در این معادله، a و b، طول اضلاع مجاور زاویه قائمه هستند و c، طول وتر (بلندترین ضلع) است. سادهترین نمونه یک سهتایی فیثاغورثی که در این معادله صدق کند، به ترتیب اعداد ۳، ۴ و ۵ هستند. یعنی ۵۲=۴۲+۳۲.
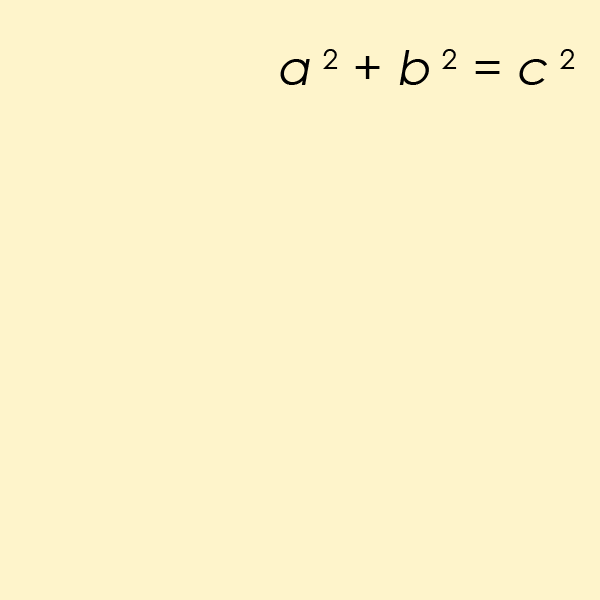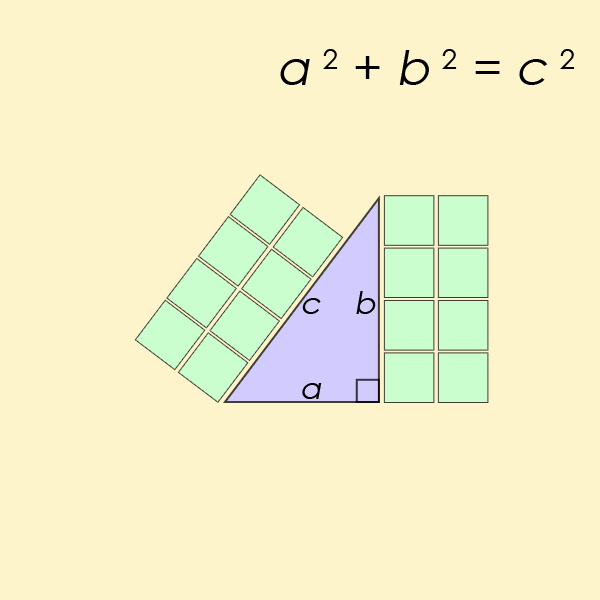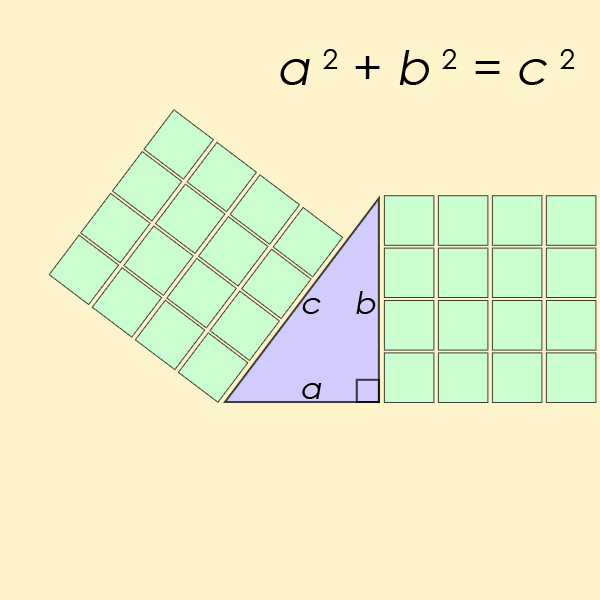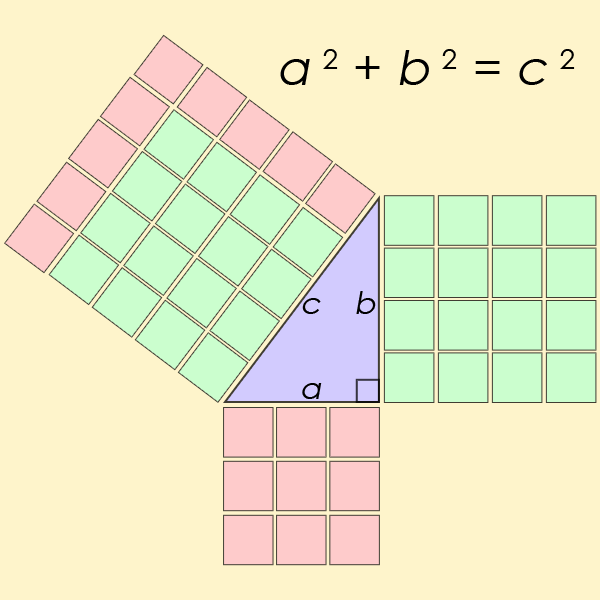
از این دستههای اعداد، میتوان برای رسم دقیق مثلثها و مستطیلهایی با زوایای قائمه استفاده کرد. اما دستگاه اعداد شصتگانی (sexagesimal) که بابلیها استفاده میکردند، کار با اعداد اول بزرگتر از ۵ را دشوار میکرد.
مانسفیلد در این باره میگوید:
این مورد یک مشکل مشخص به وجود میآورد. دستگاه اعداد پایه ۶۰ آنها، فقط اجازهی استفاده از شکلهای فیثاغورسی مشخصی را میداد.به نظر میرسد نویسنده پلیمپتن۳۲۲، تمام این اشکال را بررسی کرده تا آنهایی که مفید بودند را پیدا کند. این شناخت عمیق و عددی از کاربرد عملی مستطیلها، «پیشا مثلثات» نامگذاری شده ولی باید توجه داشت که با مثلثاتی که امروزه از آن استفاده میکنیم و شامل سینوس، کسینوس و تانژانت است، کاملا متفاوت بوده است.
حالا به لطف Si.427 میدانیم که آنها، این سهتاییهای فیثاغورسی را برای چه کاری استفاده میکردند؛ پیادهسازی حدود اراضی.
همهی اینها در دورهای اتفاق افتاده که مفهوم مالکیت زمین در حال شکلگیری بوده است. مردم شروع به نگاه به زمین به صورت «زمین من و زمین تو» کردند و میخواستند مرز مشخصی برای زمینهای خود تعیین کنند تا دچار اختلاف ملکی با همسایگانشان نشوند.این دقیقا همان چیزی است که این لوح میگوید؛ زمینی تقسیم شد و مرزهای جدیدش مشخص شدند.
لوحهای دیگری از این دوره، نشان میدهند که چرا این موضوع تا این حد اهمیت داشته است. در لوح دیگری، به مشاجرهای بین دو فرد بر سر تعدادی درخت نخل که در مرز بین دو زمین کشاورزی قرار داشتند، اشاره شده، که حاکم محلی دستور به اعزام یک نقشهبردار برای پایان اختلاف داده است. به روشنی میتوان فهمید که چرا توانایی اندازهگیری دقیق قطعات زمین تا این حد مهم بوده است.
در هر صورت، برآیند این یافتهها نشاندهنده وجود درک پیشرفتهای از هندسه نزد مردم آن دوره است. شاید این درک به اندازه آنچه بعدها دانشمندان یونان باستان به آن دست یافتند، پیشرفته نباشد، اما حاکی از این است که دانش ریاضی، فرایندی تدریجی را تا رسیدن به فیثاغورس، اقلیدس و ارشمیدس طی کرده است.
مانسفیلد در پایان میگوید: «هیچکس تصور نمیکرد که بابلیها از سهتاییهای فیثاغورسی به این صورت استفاده کرده باشند. به نظر میرسد ریاضیات محض همواره از مشکلات همان دوره الهام گرفته است.»