الگوریتمی که می‌تواند توالی‌های جذاب ریاضی برای انسان را تشخیص دهد

یکی از نادرترین ویژگی‌های ریاضیات زیبایی آن است؛ اما درک منظور دقیق ریاضیدانان از زیبایی کار دشواری است. شاید مشهورترین مثال رابطه‌ی اویلر، باشد که ارتباط عمیق بین حوزه‌های غیرمرتبط علم ریاضی را آشکار می‌کند. برای مثال از هندسه می‌آید، e و i از جبر می‌آیند و اعداد ۰ و ۱ همراه با عملگرهای + و = از نظریه‌ی اعداد گرفته می‌شوند.

تمام این اجزا به روشی ساده و غیرمنتظره یکی از شگفتی‌های بزرگ جهان ریاضیات را تشکیل می‌دهند. در نتیجه می‌توان گفت الگوهای ریاضی هم می‌توانند جذاب باشند. تشخیص این الگوهای جذاب یکی از قابلیت‌های منحصر‌ به فرد انسان است.

از سویی در سال‌های اخیر، ماشین‌ها به ابزار قدرتمندی برای تشخیص الگو تبدیل شده‌اند و حتی در مواردی مثل تشخیص چهره، تشخیص اشیا و انواع نقش‌های بازی نسبت به انسان برتری دارند. در نتیجه این سؤال‌ها مطرح می‌شوند: آیا الگوریتم‌های یادگیری ماشین می‌توانند الگوهای برجسته و جذاب ریاضیات را شناسایی کنند؟ آیا می‌توانند داوری برای سنجش زیبایی ریاضی باشند؟

حالا به لطف پروژه چای وا وو در مرکز پژوهشی واتسون تی جی IBM در نیویورک می‌توان به این سؤال‌ها پاسخ داد. وو موفق به ساخت یک الگوریتم یادگیری ماشین شده است که می‌تواند انواع ساختارهای زیبای ریاضی را شناسایی کند و از این ساختارها به عنوان فیلتری برای تفکیک توالی‌های جذاب از توالی‌های تصادفی استفاده کند.

در این روش از یک پایگاه‌ داده‌ی عجیب به نام دایره‌المعارف آنلاین توالی اعداد صحیح (OEIS) استفاده می‌شود. این پایگاه داده در دهه‌ی ۱۹۶۰ توسط ریاضی‌دانی به نام نیل اسلون ساخته شد و در سال ۱۹۹۶ روی وب قرار گرفت.

توالی صحیح برابر است با یک مجموعه از اعداد که بر اساس یک قانون مرتب شده‌اند. نمونه‌های معروف شامل اعداد اول (اعدادی که تنها بر خود و ۱ بخش‌پذیر هستند، A000040)، اعداد فیبوناچی (در این مجموعه هر عدد برابر است با مجموع دو عدد قبلی A000045)، و همین طور نمونه‌های جزیی از جمله توالی اعداد فرد یا اعداد اولی است که با عدد ۷ شروع می‌شوند.

در واقع ریاضیدان‌هایی که از OEIS (دایره المعارف توالی اعداد صحیح) استفاده می‌کنند در سطح وسیعی به دنبال توالی‌های جذاب هستند و مجموعه‌ی وسیعی از نمونه‌های معنادار فرهنگی را درنظر می‌گیرند. برای مثال می‌توان به اعداد اول با توالی ۶۶۶ اشاره کرد که بر اساس متون تاریخی معادل با عدد چهارپا است.

امروزه، پایگاه‌داده‌ی Integer Sequence شامل ۳۰۰٬۰۰۰ توالی است و روزانه تعداد زیادی از افراد آماتور و حرفه‌ای توالی‌های جدیدی را ثبت می‌کنند. تعداد زیادی از این توالی‌ها به مسائل جدید و جذاب ریاضیات اشاره می‌کنند. هدف وو یافتن راهی برای تفکیک توالی‌های جذاب از توالی‌های تصادفی بود و برای این کار به دنبال قوانین تجربی بود که به عنوان معیارهای جذابیت برای تفکیک توالی‌ها عمل می‌کنند. وو می‌گوید:

قوانین تجربی، قضیه‌های ریاضی نیستند بلکه مشاهدات تجربی روابطی هستند و بر تعداد زیادی از مجموعه‌داده‌های ساختگی و طبیعی اعمال می‌شوند. برای مثال می‌توان به قانون مور در مهندسی برق و اصل ۲۰/۸۰ پارتو در اقتصاد اشاره کرد؛ اما چرا این قوانین به درستی شناخته و درک نشده‌اند و فقط اجرا می‌شوند.

قانون بن‌فورد یکی از اصول تجربی است که بر تعداد زیادی از مجموعه‌های داده‌ای اعمال می‌شود. این قانون توسط ریاضی‌دان و ستاره‌شناس کانادایی سیمون نیوکام در سال ۱۸۸۱ کشف شد. به عقیده‌ی نیوکام صفحات اول کتاب‌های جدول لگاریتم بیشتر از صفحات آخر خوانده می‌شوند و این یعنی لگاریتم‌هایی که با عدد ۱ شروع می‌شوند رایج‌تر هستند.

بر همین اساس او این اصل را تعریف می‌کند: در هر مجموعه از داده‌ها تعداد اعدادی که با یک شروع می‌شوند بیشتر است. ایده‌ی مشابهی توسط فرانک بن‌فورد در دهه‌ی ۱۹۳۰ کشف شد و موردتوجه قرار گرفت.

قانون بن‌فورد بر یک مجموعه‌ی وسیع از مجموعه داده‌ها از جمله قبض‌های برق، آدرس خیابان‌ها، قیمت‌های انبار موجودی و چند مورد دیگر اعمال می‌شود. از این قانون می‌توان برای شناسایی خطاها در حساب‌های مالی استفاده کرد؛ اما این اصل بر توالی‌های تصادفی قابل اجرا نیست و دلیل مشخصی هم ندارد.

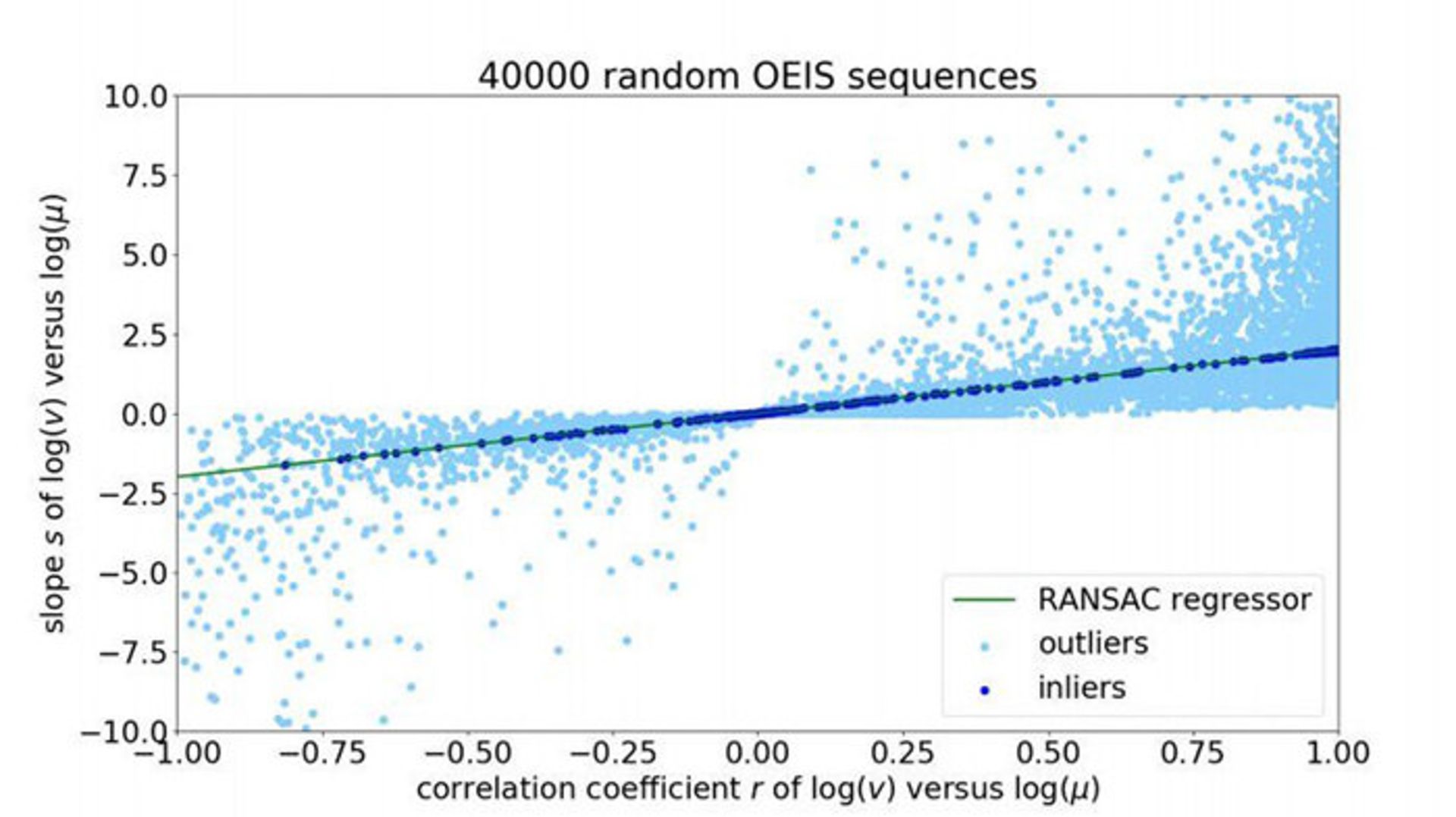
ریاضی‌دان‌ها به این نتیجه‌ رسیده‌اند که می‌توان قانون بن‌فورد را بر بعضی توالی‌های عددی صحیح اعمال کرد؛ اما تا چه اندازه می‌توان آن را تعمیم داد؟ برای پاسخ به این سؤال وو عملکرد این قانون در پیش‌بینی توزیع رقم‌های اول ۴۰٬۰۰۰ توالی را ارزیابی کرد. این توالی‌ها به‌صورت تصادفی از پایگاه‌داده‌ی OEIS انتخاب شدند.

بر اساس نتیجه‌ی به‌دست‌آمده عملکرد قانون بن‌فورد فراتر از حد انتظار بود. وو می‌گوید:

 بر اساس نتایج بسیاری از توالی‌ها (البته نه تمام آن‌ها) تا اندازه‌ای در قانون بن‌فورد صدق می‌کنند.

وو، اصل تجربی دیگری به نام قانون تایلور را هم کشف کرده است. سؤال بعدی ساده‌تر بود: آیا می‌توان از قانون بن‌فورد و قانون تایلور برای تفکیک توالی‌های تصادفی از توالی‌های موجود در OEIS استفاده کرد؟ وو برای پاسخ این سؤال ۴۰٬۰۰۰ توالی از اعداد صحیح تصادفی ساخت و این توالی‌ها را به ۴۰٬۰۰۰ توالی منتخب از OEIS اضافه کرد. سپس تفکیک توالی‌های OEIS از توالی‌های تصادفی را با قانون بن‌فورد و تایلور به الگوریتم یادگیری ماشین آموزش داد.

نتایج تأثیرگذاری به دست آمدند. درستی این الگوریتم ۰.۹۹۹ و دقت آن ۰.۹۹۸۴ است. این نتیجه در نوع خود معنادار است زیرا یک فرآیند خودکار را برای تشخیص توالی‌های جذاب تنظیم می‌کند. کاربرد این توالی‌ها کاملاً آشکار است. ریاضی‌دان‌هایی که از OEIS استفاده می‌کردند باید در طول یک سال ۱۰٬۰۰۰ تابع را پردازش میکردند و این نشان می‌دهد استفاده از این الگوریتم خودکار به سود آن‌ها بوده است.

آیا این روش می‌تواند ظرافت یا زیبایی را در ریاضیات تشخیص دهد. وو در این مورد سؤال‌هایی را مطرح می‌کند: آیا یادگیری ماشین می‌تواند مشخصه‌های کیفی دانش علمی را تشخیص دهد؛ برای مثال آیا می‌تواند یک نتیجه‌ی علمی را با درجه‌های کیفی مثل ممتاز، ساده یا جذاب ارزیابی کند؟

اگر قوانین تجربی مثل قانون بن‌فورد و تایلور شاخصی برای ارزیابی جذابیت باشند، از این الگوریتم می‌توان به عنوان سنجشی برای زیبایی یا جذابیت در یک سطح مشخص استفاده کرد. حتما اگر اویلر (ریاضی دان برجسته) الان زنده بود از وجود چنین الگوریتمی شگفت‌زده می‌شد.