یادگیری عمیق به درک چگونگی عملکرد جهان کمک می‌کند

این هفته، جامعه‌ی محققین هوش مصنوعی به‌مناسبت کنفرانس بین‌المللی دستاوردهای یادگیری (ICLR که آی‌کلیر «eye-clear» تلفظ می‌شود)، در نیواورلئان ( New Orleans) دور هم جمع شدند. این کنفرانس، یکی از گردهمایی‌های بزرگ سالانه‌ی محققین این حوزه محسوب می‌شود. مشارکت ۳ هزار محقق و ارائه ۱۵۰۰ مقاله، این همایش را به یکی از مهم‌ترین رویدادهای تبادل ایده‌ها در حوزه یادگیری عمیق تبدیل می‌کند.

عمده‌ی مقالات پذیرفته‌شده و سخنرانی‌های همایش امسال، پیرامون حل‌وفصل چهار چالش مهم یادگیری عمیق (Deep learning)، یعنی نااُریب بودن (به صفر رساندن ضریب خطای عملکرد)، امنیت، تعمیم‌پذیری و علیت هستند. در این مقاله، از بحث پیرامون چگونگی اریب‌داری و مستعدبودن الگوریتم‌های یادگیری مایشن (machine-learning) فعلی برای حملات خراب‌کارانه و محدودشدن ناباورانه‌ی آن‌ها، به تواناییشان در تعمیم الگوهایی که در داده‌‌های آموزشی، برای اپلیکیشن‌های چندگانه پیدا می‌کنند، صرف‌نظر شده و به چالش نهایی یعنی «علیت»پرداخته می‌شود؛ چراکه درحال حاضر نیز، جامعه‌ی یادگیری ماشین مشغول توسعه‌ی این فناوری جهت برطرف‌کردن ضعف‌های یادشده است.

«علیت» موضوعی است که برای مدت‌ طولانی، ذهن محققین را به خود مشغول کرده است. یادگیری ماشین، توانایی زیادی در پیداکردن همبستگی داده‌ها دارد؛ اما آیا می‌تواند روابط علت و معلولی در داده‌ها را نیز کشف کند؟

چنین دستاوردی می‌تواند نقطه‌ی عطف بزرگی باشد؛ چراکه اگر الگوریتم‌ها بتوانند درمورد علل و اثرات پدیده‌های مختلف در سیستم‌های پیچیده به ما کمک کنند، فهم ما از جهان را عمیق‌تر می‌کنند و ابزار قدرتمندی برای تاثیرگذاری در آن، دراختیار ما قرار می‌دهند.

لئون بوتو (Léon Bottou)، محقق تحسین‌شده‌ی واحد تحقیقات هوش مصنوعی فیسبوک و دانشگاه نیویورک، در نشست روز دوشنبه، چارچوبی از چگونگی دستیابی به هدف فوق ارائه کرد. در ادامه، خلاصه‌ای از نظرات او را با هم می‌خوانیم.

اولین نظریه‌ی مهم بوتو به شرح زیر است: فرض کنید می‌خواهید یک سیستم بینایی کامپیوتری طراحی کنید که بتواند اعداد دست‌نویس را شناسایی کند (این یک مسئله مقدماتی کلاسیک است که به‌طور گسترده در مجموعه‌ داده‌های «MNIST» که در تصویر زیر مشاهده می‌کنید، استفاده می‌شود). می‌توانید با یک شبکه‌ی عصبی (neural-network)، روی مجموعه‌ی گسترده‌ای از تصاویر اعداد دست‌نویس، که هر کدام با عدد نشان‌داده‌شده در تصویر علامت‌گذاری شده‌اند، شروع کنید ودر پایان سیستم مناسبی داشته باشید که قادر باشد تصاویری را که قبلا مشاهده نکرده است، شناسایی کند.

مجموعه داده‌ی MNIST 

اما دوباره فرض کنید که مجموعه داده‌ی شما کمی‌ تغییر کرده است و هر کدام از اعداد دست‌نویس دارای رنگ‌های قرمز یا سبز هستند. تصور کنید نمی‌دانید کدام‌یک از دو روش رنگ یا شکل علامت‌گذاری، پیش‌بینی‌کننده‌ی بهتری برای عدد نوشته‌شده در تصویر است. روش استانداردی که امروزه به‌کار گرفته می‌شود، این است که هر بخش از مجموعه‌ی داده‌ها را به هر دو شکل فوق، برچسب‌گذاری کند و به شبکه‌ی عصبی می‌دهند تا تصمیم بگیرد.

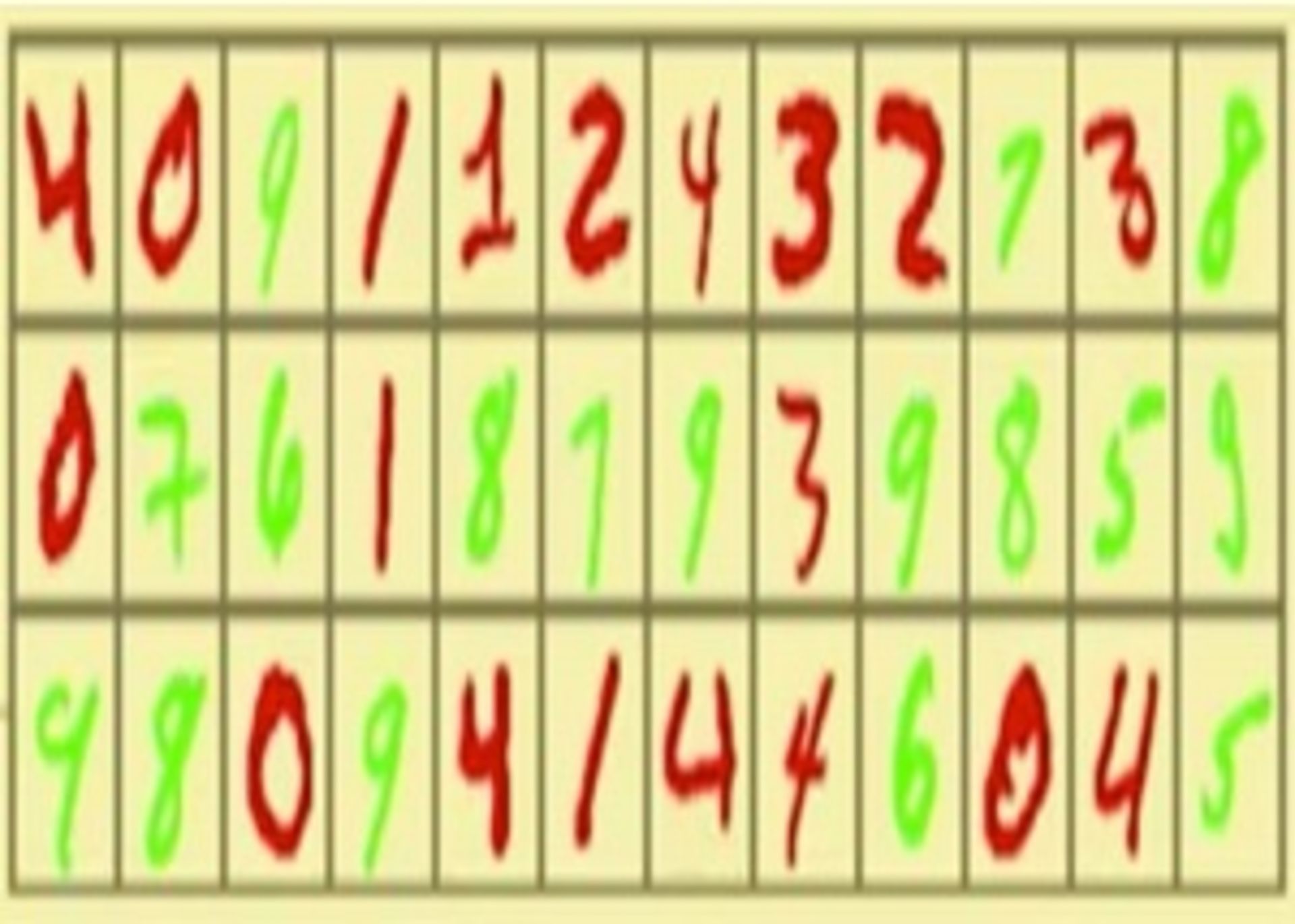
     مجموعه داده‌ی رنگی MNIST                         

در این صورت، بحث جالب خواهد شد. مجموعه‌ی داده‌ی «MNIST رنگی» گمراه‌کننده تلقی می‌شود؛ چراکه در جهان واقعی، رنگ عدد کاملا بی‌معنی است، اما در این مجموعه داده‌ی خاص، رنگ، پیش‌بینی‌کننده‌ی بسیار بهتری نسبت‌به «شکل» است. بنابراین، شبکه‌ی عصبی ما یاد می‌گیرد که از رنگ به‌عنوان پیش‌بینی‌کننده‌ی اصلی استفاده کند. تا زمانی‌که از این شبکه‌ی عصبی برای شناسایی اعداد دست‌نویس دیگری استفاده کنیم که از الگوی رنگ مشابهی پیروی می‌کنند، این روش جواب می‌دهد؛ اما اگر رنگ‌ها را عوض کنیم، عملکرد سیستم کاملا افت پیدا می‌کند (بوتو این آزمایش را با داده‌های واقعی و شبکه‌ی عصبی واقعی انجام داد، در حالت اول میزان تشخص درست ۸۴/۳ درصد و در حالت دوم تنها ۱۰ درصد بود).

به عبارت دیگر، این شبکه‌ی عصبی به نظر بوتو یک «همبستگی جعلی» را می‌سازد؛ که باعث می‌شود خارج از حوزه‌ای که آموزش دیده است، کاملا بی‌فایده باشد. در حالت نظری، اگر شما بتوانید همه‌ی همبستگی‌های جعلی را در یک مدل یادگیری ماشین از بین ببرید، تنها با حالت‌های «ثابتی» مواجه خواهید بود؛ حالت‌هایی که بی‌توجه به زمینه همواره درست هستند.

بوتو اضافه می‌کند که درعوض، ثبات به شما اجازه می‌دهد تا علیت را درک کنید. اگر ویژگی‌های ثابت یک سیستم را بدانید و از مداخله‌ای که روی سیستم صورت گرفته است، اطلاع داشته باشید؛ باید بتوانید نتیجه این مداخله را حدس بزنید. مثلا، اگر بدانید همیشه شکل یک عدد دست‌نویس معنی آن را تعیین می‌کند، می‌توانید نتیجه بگیرید که تغییرشکل آن (علت)، معنای آن (معلول) را تغییر می‌دهد. به‌عنوان مثال دیگر، اگر بدانید تمام اشیاء از قانون گرانش تبعیت می‌کنند، می‌توانید نتیجه بگیرید که اگر توپی را رها کنید (علت)، به زمین خواهد افتاد (معلول).

بدیهی است که این‌ها، مثال‌های ساده‌ای از روابط علت و معلولی بر پایه‌ی ویژگی‌های ثابت هستند که هم‌اکنون نیز می‌دانیم؛ اما چگونه می توانیم این ایده را به سیستم‌های پیچیده‌ای که هنوز درک نمی‌کنیم تعمیم دهیم؟ به‌عنوان مثال، اگر می توانستیم ویژگی‌های ثابت سیستم‌های اقتصادی را پیدا کنیم، قادر می‌شدیم اثرات پیاده‌سازی سیاست درآمد پایه‌ی جهانی را درک کنیم؛ یا با یافتن ویژگی‌های ثابت سیستم آب‌وهوای جهان، اثرات اقدامات مهندسی آب‌وهوای (geoengineering) مختلف را ارزیابی کنیم.  

چگونه می‌توان از شر همبستگی جعلی رها شد؟ جواب این سؤال در نظریه‌ی مهم دیگر بوتو نهفته است. در آموزش یادگیری ماشین کنونی مرسوم است که داده‌های متنوع و مختلف را تا حد ممکن، در داخل یک مجموعه‌ی آموزشی قرار می‌دهند. اما به‌نظر بوتو، این روش می‌تواند زیان‌بار باشد و داده‌هایی که از زمینه‌های مختلف، چه از نظر زمانی و چه مکانی یا در شرایط آزمایشی مختلف جمع می‌شوند، به‌جای ترکیب شدن باید به‌عنوان مجموعه‌های مستقلی درنظر گرفته شوند؛ چراکه در صورت ترکیب شدن، همان‌طور که اکنون معمول است، اطلاعات ضمنی مختلفی از بین می‌روند و احتمال نمایان شدن همبستگی‌های جعلی افزایش پیدا می‌کند.

اجازه دهید بار دیگر به مثال ساده‌ی MNIST رنگی برگردیم. بوتو به‌منظور تشریح نظریه‌ی خود برای پیدا کردن ویژگی‌های ثابت، آزمایش اصلی خود را دوباره اجرا کرد. این‌بار، او دو مجموعه‌ داده‌ی MNIST رنگی با دو الگوی رنگ متفاوت را استفاده کرد، سپس به شبکه‌ی عصبی خود آموزش داد تا یک همبستگی که در هر دو گروه صادق است را پیدا کند. وقتی بوتو این مدل بهبودیافته را برای اعداد جدید با الگوهای رنگی یکسان و متفاوت آزمایش کرد، میزان تشخیص درست برای هر دو حالت ۷۰ درصد شد. نتایج نشان داد که شبکه‌ی عصبی یاد گرفته است رنگ را نادیده بگیرد و تنها روی شکل علامت‌گذاری تمرکز کند.

بوتو می‌گوید کارش روی این نظریه‌ها تمام نشده است و مدتی طول خواهد کشید تا جامعه‌ی محققین این تکنیک‌ها را روی مسائل پیچیده‌تر از اعداد رنگی نیز آزمایش کند. اما چارچوب کلی این آزمایش‌ به ظرفیت یادگیری عمیق جهت کمک به درک چرایی اتفاق افتادن حوادث و افزایش کنترل ما روی سرنوشتمان اشاره دارد.