۱۲ مورد از بحث برانگیزترین معماهای ریاضی (قسمت سوم)

اگر با مبحث همگرایی سری‌ها آشنا باشید، احتمالاً از قبل می‌دانید که بسیاری از سری‌ها مانند سری زیر به یک عدد همگرا می‌شوند.

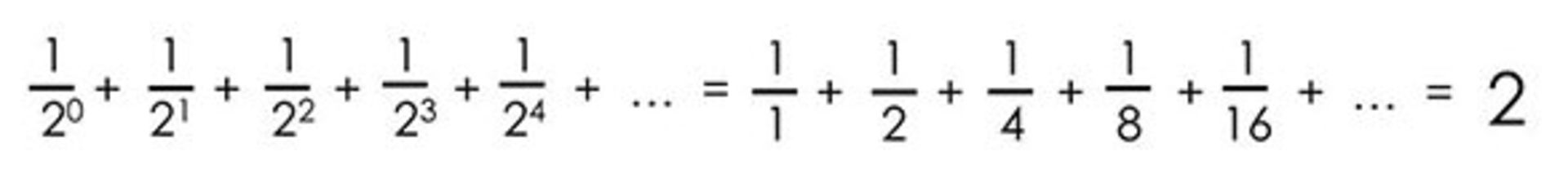
درمقابل، سری‌هایی مانند مثال زیر نیز وجود دارند که واگرا هستند یا به اصطلاح به بی‌نهایت همگرا می‌شوند.

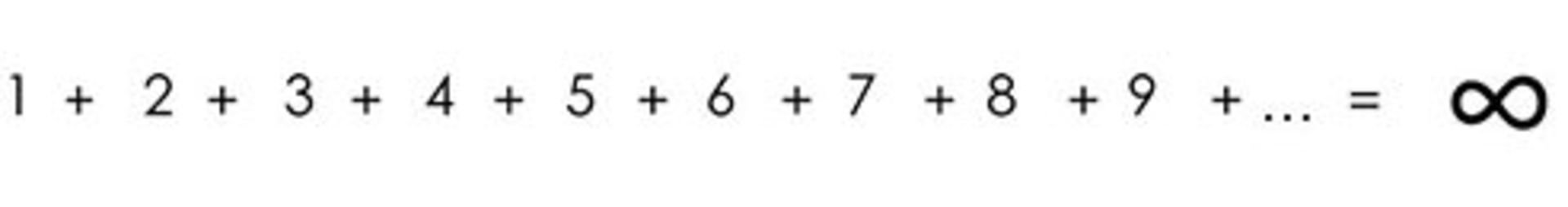
اما نظر شما درباره‌ی سری زیر چیست؟

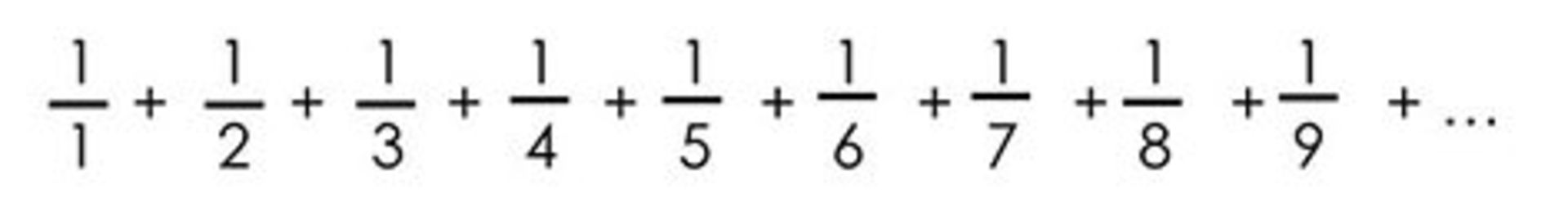
آیا این سری‌ هم مانند مثال اول به یک عدد همگرا می‌شود یا مانند مثال دوم واگرا است؟

سری بالا که سری هارمونیک نام دارد بر خلاف باور بسیاری از افراد یک سری واگرا است. درست است که با بزرگ شدن مخرج کسر تا بی‌نهایت، جملات به سمت صفر میل می‌کنند، اما سری هارمونیک با روندی بسیار بسیار آهسته به بی‌نهایت می‌رود.

اثبات آن نیز به این صورت است:

بیایید سری هارمونیک را با یک سری کوچک‌تر از خودش مقایسه کنیم.

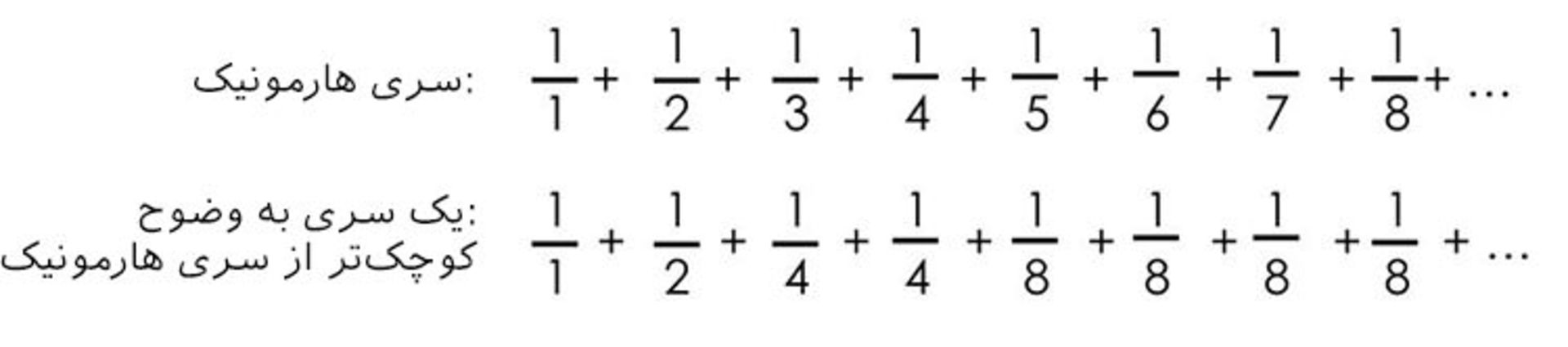
اگر دقت کنید در سری دوم، تمامی جملات کوچکتر یا مساوی با جملات سری هارمونیک است. (پس از آخرین جمله، ۸ جمله یک شانزدهم، و پس از آن ۱۶ جمله یک سی و دوم است و به همین ترتیب جملات ادامه خواهند داشت.)

حالا بیایید نگاه دقیق‌تری به سری دوم بیندازیم.

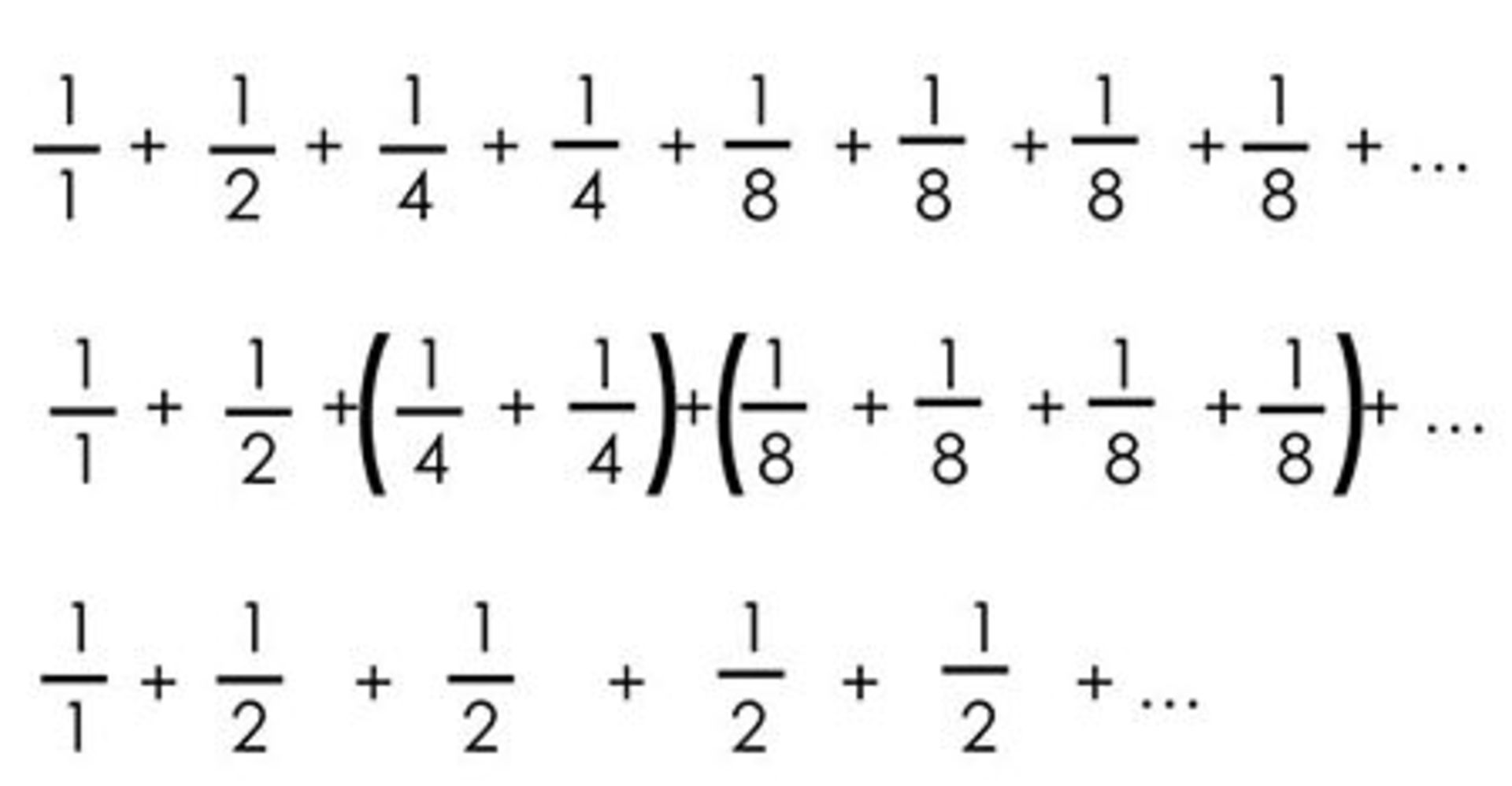
همان‌طور که مشخص است می‌توان سری دوم را به‌صورت ۱ به اضافه‌ی بی‌نهایت جمله با مقدار یک دوم بازنویسی کرد. جمع این مقادیر به وضوح بی‌نهایت می‌شود.

پس اگر

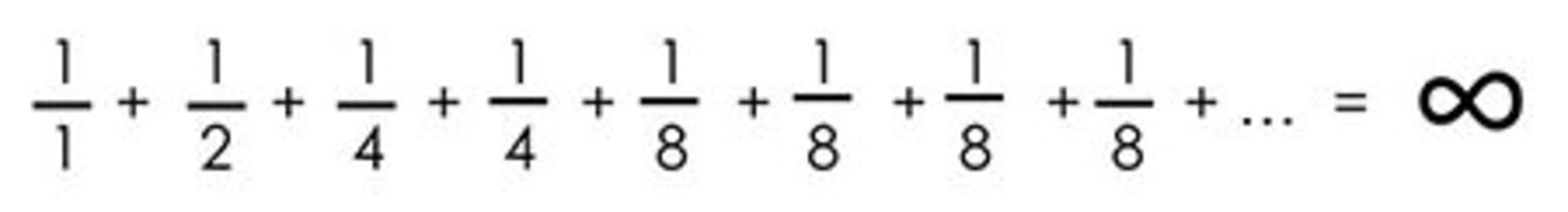
و

آنگاه

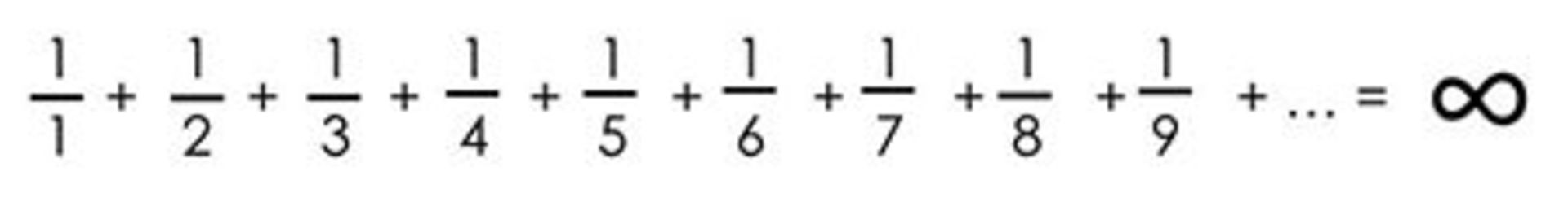
اثبات این موضوع به یک روش دیگر را نیز می‌توانید در اینجا مطالعه کنید.

آیا احتمال اینکه شما نسبت به دوستان‌تان، از تعداد دوستان بیشتری برخوردار باشید بیشتر است؛ یا دوستان‌تان احتمالاً به‌صورت میانگین تعداد دوستان بیشتری از شما خواهند داشت؟ یا اینکه فکر می‌کنید وقتی صحبت از «تصادفی» و «میانگین» به میان می‌آید، دو احتمال مطرح شده در بالا با هم برابر است و نمی‌توان از قبل درباره‌ی تعداد دوستان یک نفر نسبت به رفقایش اظهار نظر کرد؟

جواب مسئله‌ی بالا به این صورت بیان می‌شود:

«تعداد دوستان اکثر افراد، از میانگین تعداد دوستان رفقایشان کمتر است!»

اما جمله‌ی بالا به چه معنا است؟ عبارت فوق به زبان ساده یعنی اگر یک نفر را به‌صورت تصادفی انتخاب کنیم، به احتمال زیاد نسبت به دوستان خود از تعداد کمتری دوست برخوردار است.

این پدیده که مربوط به ریاضیات کاربردی است، با توجه به خواص ریاضی «شبکه‌های اجتماعی» توجیه می‌شود.

در نگاه اول به نظر می‌رسد که وقتی یک نفر را به‌صورت تصادفی انتخاب کنیم، احتمال اینکه شخص مورد نظر از دوستان خود مشهورتر باشد (دوستان بیشتری داشته باشد) یا اینکه دوستانش از اون مشهورتر باشند (دوستان بیشتری داشته باشند) نباید با هم تفاوتی داشته باشد.

در مقاله‌ای که در سال ۱۹۹۱ توسط اسکات فلد جامعه شناس منتشر شد، ۷۴ درصد افراد دوستان کمتری نسبت به میانگین تعداد دوستان رفقایشان داشتند. نکته‌ی اساسی در اینجا «افراد مشهور» هستند.

بیایید یک مثال را با هم بررسی کنیم. شبکه‌ی دوستی زیر را در نظر بگیرید:

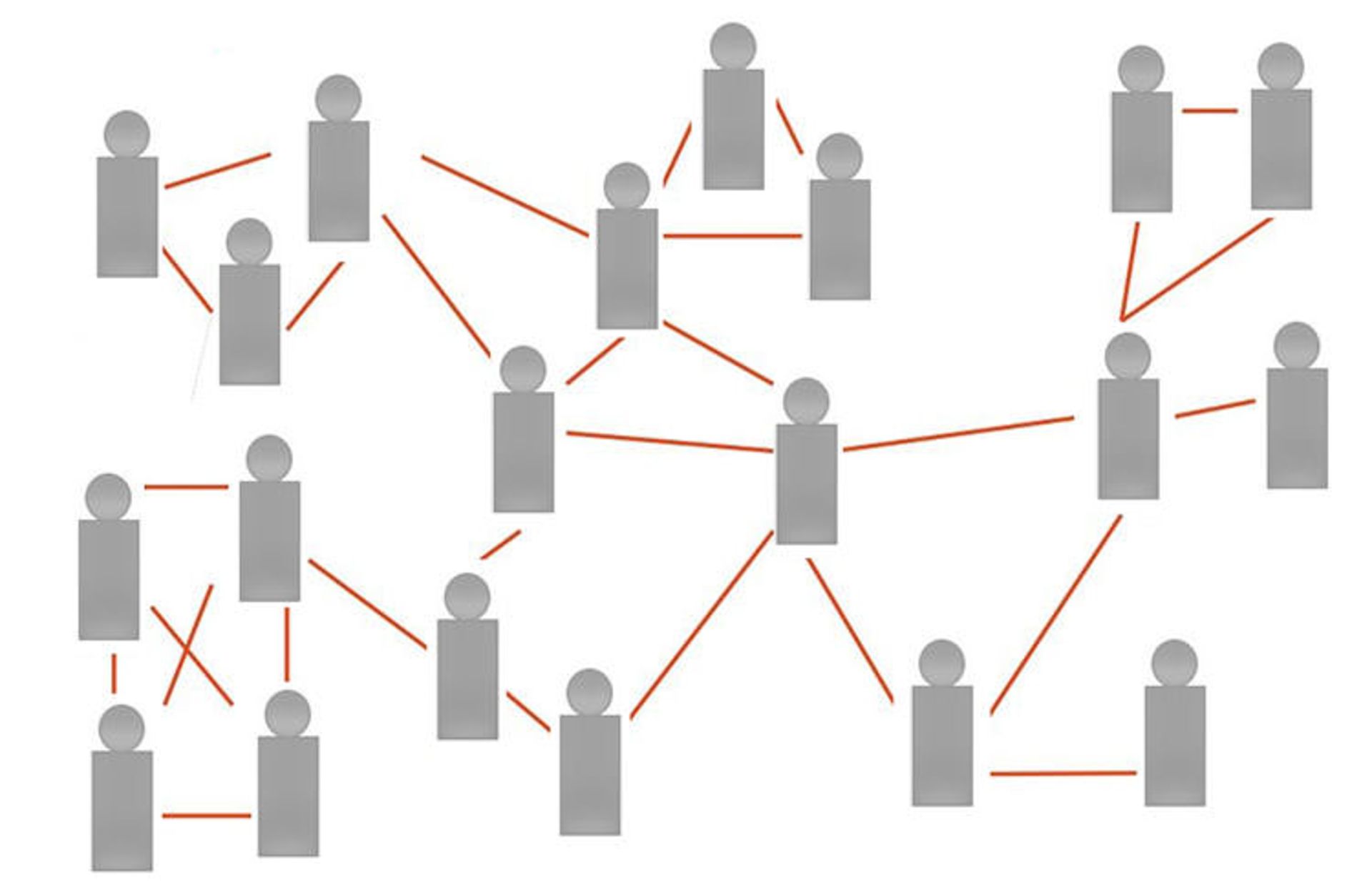
در این شبکه هر نفر به‌صورت میانگین ۲.۸۵ دوست دارد، اما دوست هر نفر به‌صورت میانگین ۳.۳۹ دوست دارد. این مورد تنها یک مثال برای نشان دادن «ممکن» بودن چنین حالتی است، اما از آن برای اثبات این اصل به‌صورت کلی نمی‌توان استفاده کرد.

تا قبل از ظهور «شبکه‌های اجتماعی آنلاین»، تحقیق درباره‌ی صحت این حقیقت کار دشواری بود، اما با آمدن فیسبوک، توییتر و اینستاگرام، به‌راحتی می‌توان درستی پاسخ ارائه شده به این مسئله را بررسی کرد.

مسئله‌ی فوق به پارادوکس دوستی مشهور است و با استفاده از نامساوی کوشی-شوارتز می‌توان آن را به‌راحتی اثبات کرد. می‌توانید اینجا در این باره بیشتر بخوانید. مقاله‌ی اسکات فلد در این رابطه را نیز می‌توانید از اینجا دانلود کنید.

یک چهار ضلعی دلخواه رسم کنید. این چهارضلعی می‌تواند مقعر، محدب، نامنظم و به‌طور کلی به هر شکلی که دوست دارید باشد؛ تنها کافی است چهار ضلعی مورد نظر از چهار زاویه و خطوط راست تشکیل شده باشد.

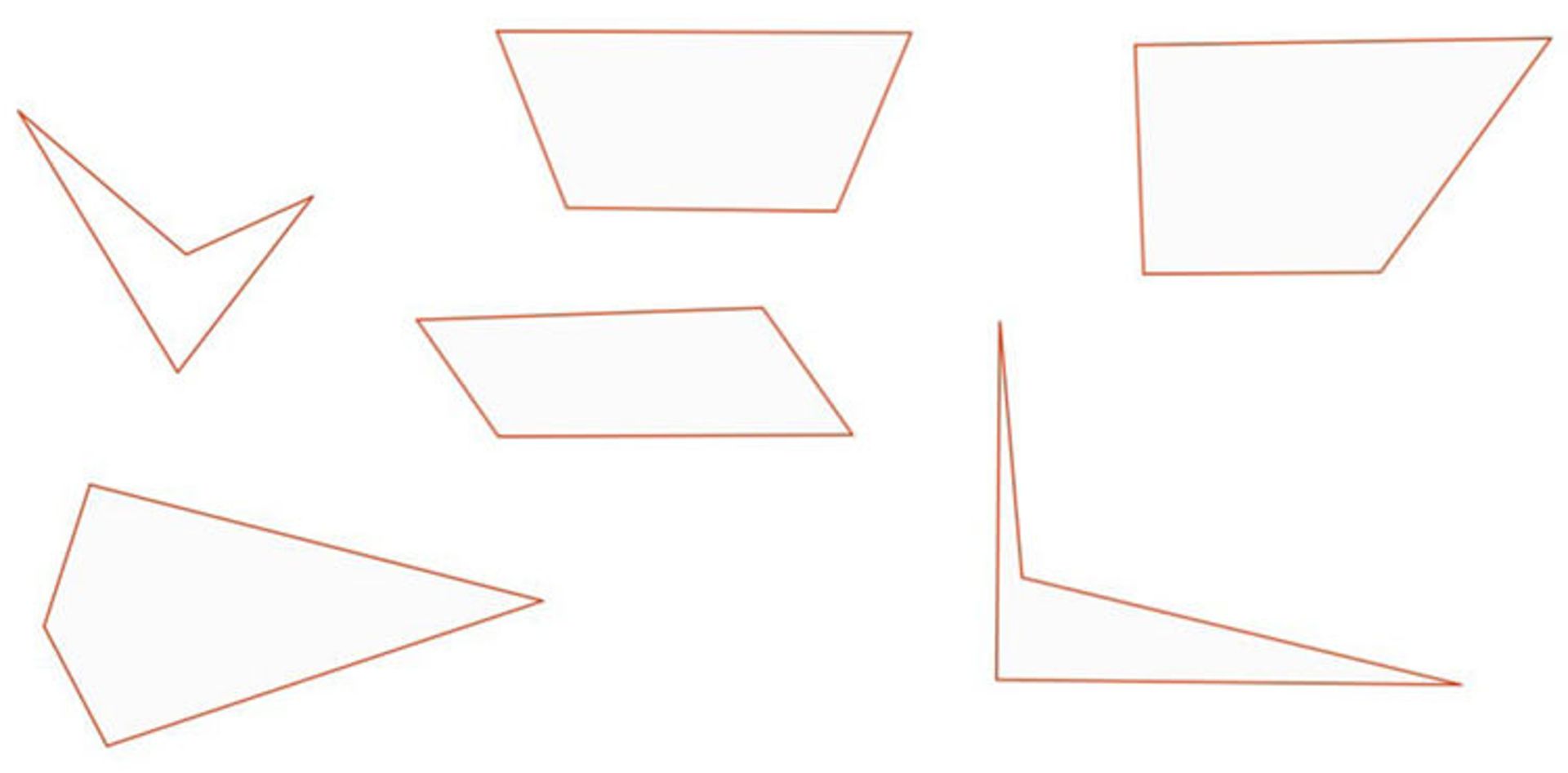
نقطه‌ی میانی هر ضلع را پیدا کرده و آن‌ها را به یکدیگر متصل کنید.

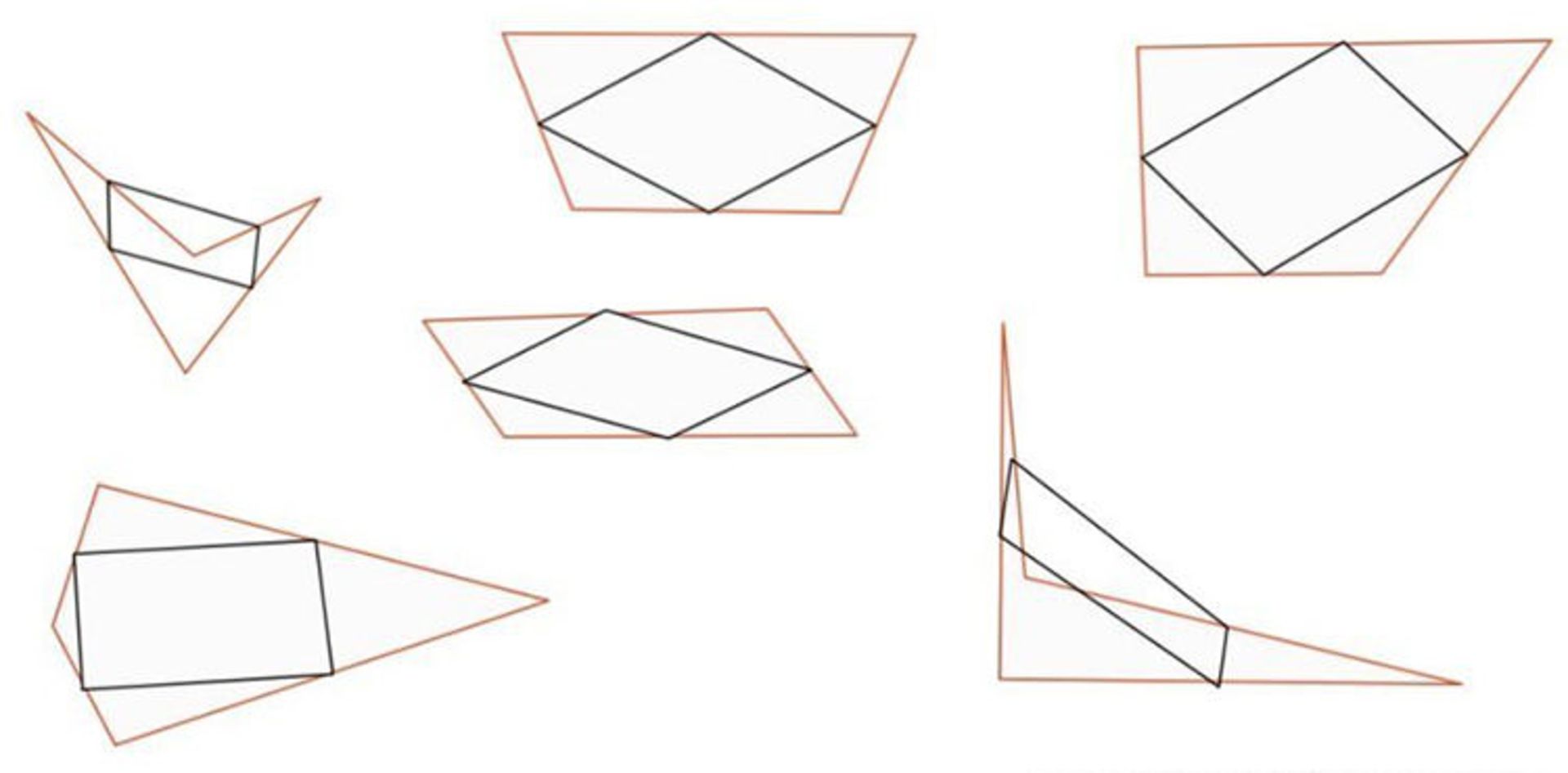
همان‌طور که می‌بینید، نتیجه همواره یک متوازی الاضلاع است.

سه زندانی در سه سلول جدای از هم هستند و هر سه محکوم به اعدام شده‌اند. قاضی به‌صورت تصادفی یکی از زندانی‌ها را عفو می‌کند. نگهبان می‌داند که کدام زندانی مشمول عفو شده است، اما از گفتن نام او خودداری می‌کند.

زندانی A که خیلی دوست دارد بداند فردا قرار است اعدام شود یا خیر، از نگهبان می‌پرسد که به او بگوید کدام یک از دو زندانی B و C قرار است اعدام شود. سؤال او از نگهبان به این صورت است:

که اگر B عفو شده است، نام C را به من بگو و اگر C عفو شده، نام B را به من بگو. اگر هم من عفو شده‌ام، سکه‌ای بینداز و بین B و C نام یکی را به‌صورت تصادفی بگو.

نگهبان نام زندانی B را می‌گوید.

زندانی A خوشحال شده و با خود فکر می‌کند که شانس عفو شدن او از یک سوم به یک دوم افزایش یافته است، چراکه گزینه‌هایی که ممکن است مورد عفو قرار بگیرند، تنها از بین A و C خواهند بود.

زندانی A در این باره به زندانی C خبر می‌دهد تا او را نیز خوشحال کند. زندانی C از زندانی A هم خوشحال‌تر می‌شود و به او می‌گوید:

شانس تو برای عفو شدن همچنان یک سوم است، درحالی‌که شانس من به دو سوم افزایش یافته است.

حق با کدام زندانی است؟

هر سه زندانی در ابتدا یک سوم شانس عفو داشتند. نگهبان نام B را بر زبان آورده است که با توجه به سؤال زندانی، می‌تواند یکی از دو معنای زیر را داشته باشد:

• C قرار است عفو شود (شانس یک سوم)
• A قرار است عفو شود و نام B با توجه به سکه انداختن گفته شده است. (شانس یک ششم)

این یعنی شانس اینکه A عفو شود نصف شانس عفو C است. B نیز هیچ شانسی برای عفو ندارد و محکوم به فنا است. با توجه به اینکه مجموع احتمال باید برابر ۱ شود، پس احتمال عفو A همان یک سوم و احتمال عفو C دو سوم است.

اگر تجزیه و تحلیل جملات بالا برایتان سخت است، در زیر پاسخ معما را به‌صورت تصویری با هم مرور خواهیم کرد. شکل زیر تمام حالات ممکن قبل از انداختن سکه را نشان می‌دهد:

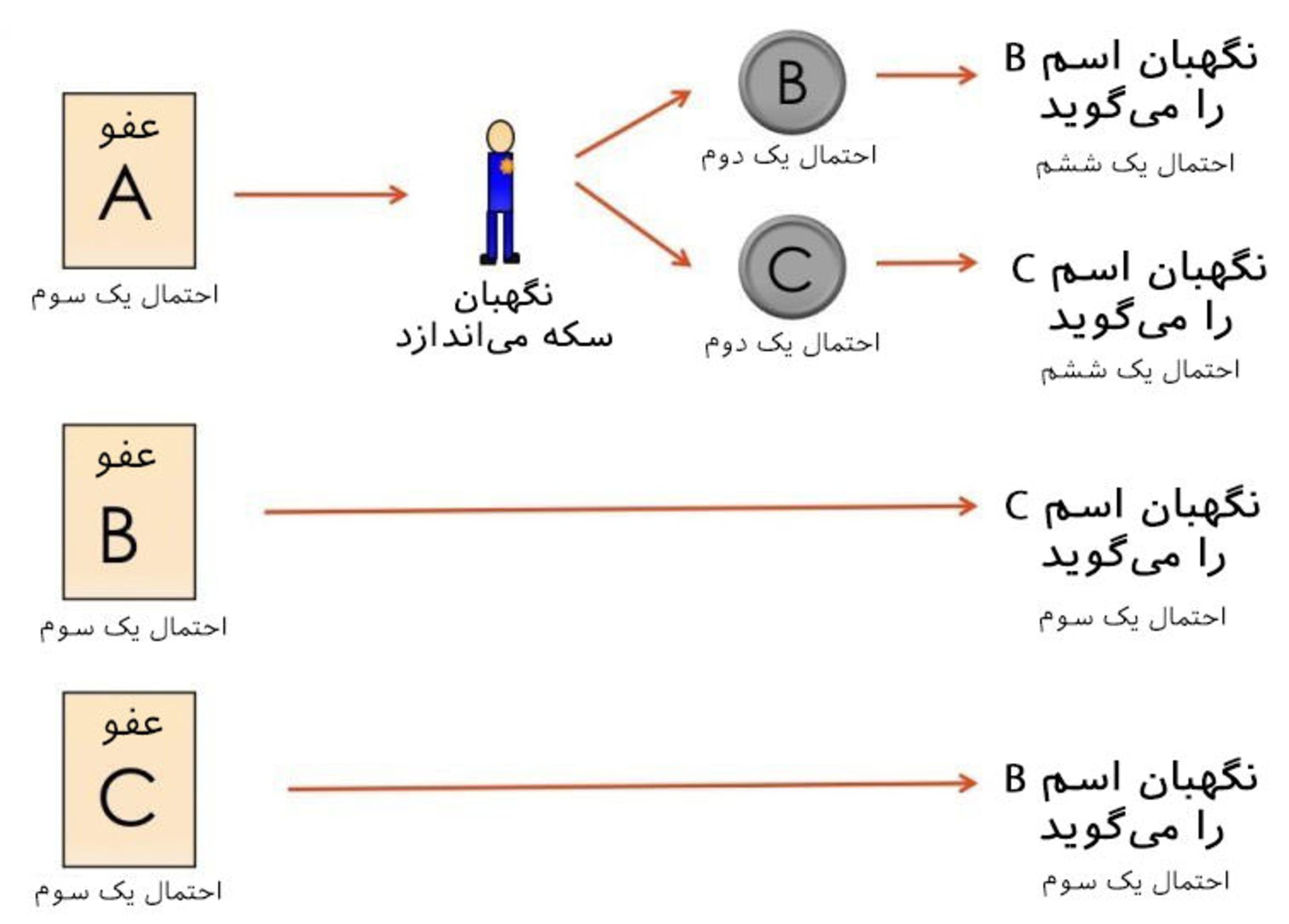
ازآنجاکه نگهبان نام B را گفته است، تنها با این حالات رو‌به‌رو هستیم:

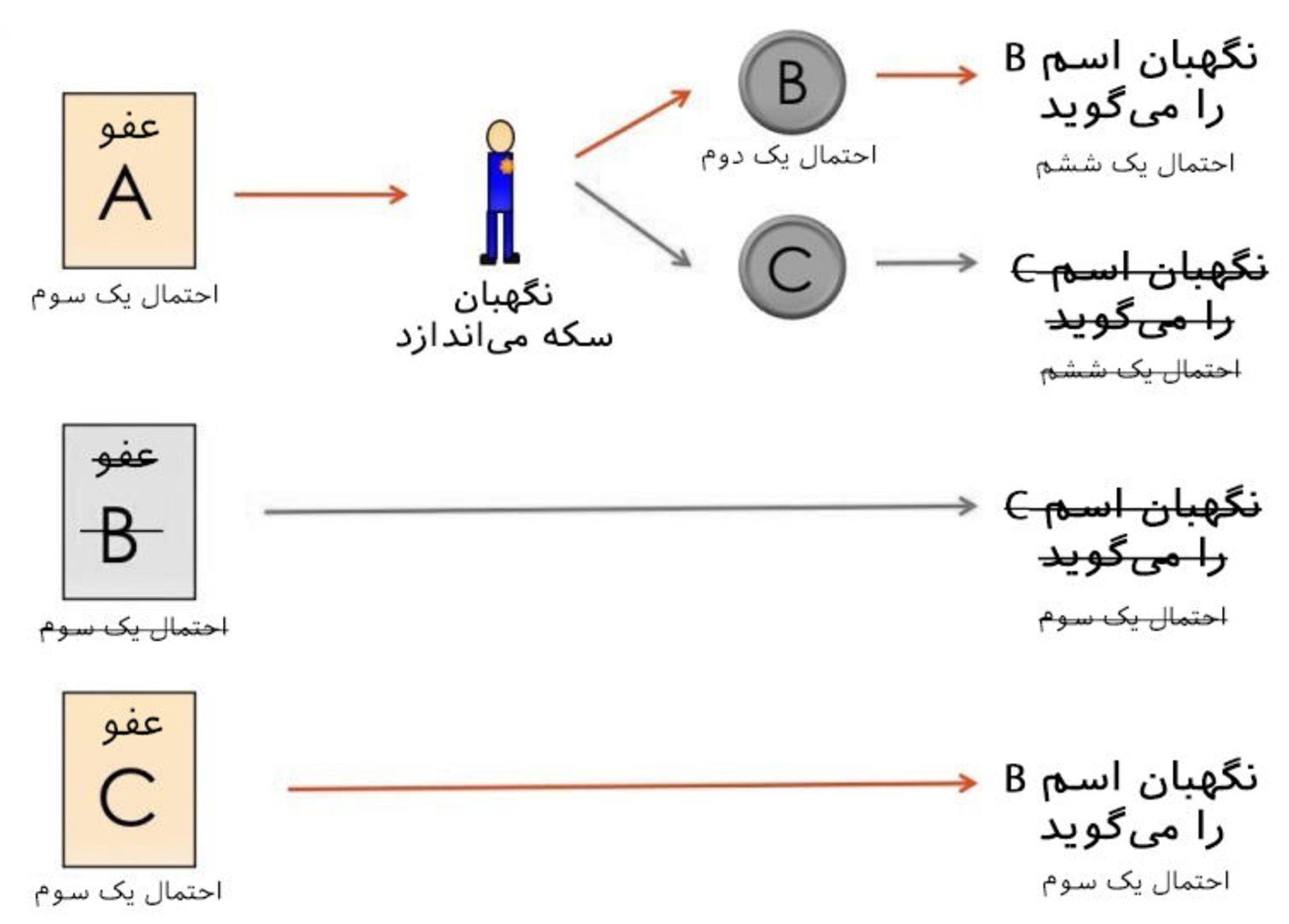
همان‌طور که در تصویر بالا می‌بینید شانس B برای عفو به 0 کاهش یافته و شانس C دو برابر شانس B است. در اینجا می‌توانید درباره‌ی معمای سه زندانی بیشتر بخوانید.

معماهایی که در این مجموعه مطرح شدند، همگی با استفاده از قوانین ابطال ناپذیر ریاضی قابل اثبات هستند. جدای از اثبات ریاضی، در مواردی که امکان شبیه‌سازی مسئله در دنیای واقعی وجود دارد، می‌توان به روش آماری نشان داد که احتمالات به دست آمده (برای مثال در معمای مانتی‌هال، مسئله‌ی تاریخ تولد، جعبه‌ی برتراند و معمای سه زندانی) در عمل هم برابر با همان مقداری است که پاسخ ریاضی مسئله پیش‌بینی کرده است.

پال اردیش ریاضی‌دان مجارستانی، یکی از کسانی است که بیشترین تعداد مقالات علمی منتشر شده در طول تاریخ به نام او ثبت شده است. حتی این ریاضی‌دان برجسته هم تنها پس از اینکه با چشمان خودش دید که در شبیه‌سازی کامپیوتری معمای مانتی هال، در صورت تعویض در در دو سوم موارد برنده می‌شوید، حاضر به پذیرش پاسخ مسئله شد.

در بررسی آماری مسائل احتمال، یک مسئله هزاران یا میلیون‌ها بار تکرار می‌شود تا ببینیم در عمل، شانس گزینه‌های مختلف چقدر است. مثلاً اگر هزاران بار سکه یا تاس بیندازیم، در عمل مشاهده خواهیم کرد که شانس هر گزینه به ترتیب برابر با یک دوم و یک ششم است. همان‌طور که در قسمت قبل اشاره کردیم، این روش به روش مونته کارلو مشهور است. اردیش نیز که یک ریاضی‌دان بود و به صحت نتایج به دست آمده توسط روش مونته کارلو اطمینان داشت، وقتی پاسخ معمای مانتی هال با استفاده از این روش را دید، اشتباه خود را پذیرفت.

اما چرا عده‌ای باوجود انبوهی از اثبات‌های ریاضی و شواهد تجربی، همچنان بسیاری از این معماها را حقه‌های ریاضی می‌دانند؟

یکی از دلایل فهم سخت مسائل احتمال، ادراکی (intuitive) نبودن چنین مسائلی است. درک مفاهیمی چون «بی‌نهایت» و بسیاری از مفاهیم احتمالات برای ذهن انسان بسیار دشوار است. ازآنجاکه ما انسان‌ها به‌صورت «غریزی» درک درستی از این مفاهیم نداریم، باید با آن‌ها ازطریق «آموزش» آشنا شویم.

استیون پینکر روانشناس در کتاب خود با نام «The Blank Slate» اینگونه استدلال می‌کند که یکی از دلایل اصلی مشکل اکثر افراد با احتمالات، زبان تخصصی و گیج کننده‌ای است که برای بیان این قبیل مسائل از آن استفاده می‌شود. می‌توانید اینجا به مطالعه‌ی بیشتر در این زمینه بپردازید.

اما دسته‌ی دیگری از افراد هستند که علاوه بر قبول نداشتن حقایق ریاضی، با اطمینان خاصی ادعای رد آن‌ها را نیز دارند. این افراد «نوابیغ» نامیده می‌شوند.

نوابیغ (با نوابغ اشتباه نشود) اصطلاحی است که عفت چهره گشا و دکتر عبادالله محمودیان، استاد ریاضیات دانشگاه صنعتی شریف و عضو انجمن ریاضی ایران، برای اشاره به کسانی که سعی در حل معماهای ناممکن یا رد اصول اثبات شده دارند، به کار برده‌اند. نوابیغ به چند دسته تقسیم می‌شوند:

• کسانی که سعی می‌کنند ناممکن‌ها را ممکن کنند: این افراد سعی دارند مسائل غیر ممکنی چون تثلیث زاویه، تربیع دایره، یا تضعیف مکعب را حل کرده یا موتور بدون سوخت بسازند.
• مدعیان حل مسئله‌های حل‌نشده‌ی معروف: کسانی که تلاش می‌کنند مسئله‌های دشوار ریاضی از جمله فرضیه گلدباخ یا کشف فرمولی برای تولید اعداد اول، را با روش‌های ابتدایی حل کنند.
• بنیانگذاران نظریه‌های بی‌اساس: کسانی که می‌خواهند نظریه‌هایی که ربطی به ریاضیات ندارند (مانند وحدانیت خدا، نامرئی کردن فیزیکی اشیاء و ...) را با استفاده از ریاضیات حل کنند.
• رد کنندگان اصول اثبات شده: افرادی که تلاش دارند اصول اثبات شده‌ی ریاضی و فیزیک را نقض کنند. از جمله ادعاهای این افراد می‌توان به درست نبودن مقدار عدد پی یا نادرست بودن قانون اول ترمودینامیک اشاره کرد.

مقاله‌ی زیبا و خواندنی دکتر محمودیان را می‌توانید از اینجا بخوانید.

قسمت‌های قبلی معماهای بحث‌برانگیز ریاضی را نیز می‌توانید از اینجا مطالعه کنید:

قسمت اول – قسمت دوم